Приложение Ж Обобщённое обращение матрицы

П.8. Обобщённое обращение матрицы

Рассмотрим теперь обобщённые обращения тех матриц, которые не имеют обратных в обычном смысле [см. (П.5.1)]. Решение совместной системы уравнений Ax=с можно получить использованием обобщённого обращения матрицы А.

Определение и свойства

Обобщённым обращением матрицы A=А_np является любая матрица A^–, удовлетворяющая условию

AA^–A=A.                                                      (П.8.1)

Обобщённое обращение не является единственным, за исключением случая, когда матрица А невырожденная. В этом случае A^–=A^–1. Обобщённое обращение называют также квазиобращением.

Каждая квадратная или прямоугольная матрица имеет обобщённую обратную матрицу. Это справедливо и для векторов. Например, пусть дан вектор

х=.

Тогда, удовлетворяющим условию (П.8.1) обобщённым обратным вектора х является x₁^–= [1, 0, 0, 0]. Другими обобщёнными обратными вектора х являются x₂^–= [0, 1/2, 0, 0], x₃^–= [0, 0, 1/3, 0] и x₄^–= [0, 0, 0, 1/4]. Для каждого вектора x_i^–, имеем

Рекомендуемые материалы

xx_i^–х=х1=х, при i =1, 2, 3, 4.

В этом пояснении; х - вектор-столбец и x_i^– - вектор-строка. Эта закономерность обобщена в следующей теореме.

Теорема П.8.1. Если матрица А размеров nxp, то любая её обобщённая обратная А^– размеров pxn.

Доказательство: По определению АА^–А=А. Если А=А_np, то для выполнения умножения А^– должна быть размеров рxn.

□

В следующем примере даются два пояснения обобщенных обращений некоторой вырожденной матрицы.

Пример П.8.1. Пусть дана матрица

А=.                                              (П.8.2)

Третья строка матрицы А представляет собой сумму первых двух строк и вторая строка не является кратной первой, следовательно, А имеет ранг 2. Даны две обобщенные обратные матрицы

А₁^–= и А₂^–=.                     (П.8.3)

Легко проверить умножением, что AА₁^–A=A и AА₂^–A=A.

□

Методы получения обобщенных обратных матриц А₁^– и А₂^– в (П.8.3) представлены в теореме П.8.2 и в следующим за ней пятиступенчатом алгоритме.

Теорема П.8.2. Пусть матрица А=А_np ранга r и она разделена на подматрицы в виде

А=,

где A₁₁ размеров rxr и ранга r. Тогда обобщённая обратная матрицы А даётся выражением

А^–=,

где три нулевые матрицы О таких размеров, что А^– размеров pxn.

Доказательство: Умножением разделённых матриц, как дано в (П.3.1), получаем

AА^–A=A=.

Чтобы показать, что A₂₁A₁₁^–1A₁₂=A₂₂, умножим А слева на матрицу

В=,

где О и I соответствующих размеров, чтобы получить

ВA=.

Матрица В невырожденная и поэтому [по пункту 2 теоремы П.4] ранг матрицы BA получен r=ранг(A). В произведении BA подматрица  имеет ранг r и, следовательно, столбцы, начинающиеся в A₁₂, являются линейными комбинациями столбцов, начинающихся в A₁₁. Эта линейная зависимость столбцов подматрицы  от столбцов подматрицы  с использованием некоторой матрицы Q может быть выражена в виде

=Q.                                  (П.8.4)

Выполняя умножение, как в (П.2.19), правая часть выражения (П.8.4) становится

=Q==

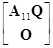
Таким образом, А₂₂–A₂₁A₁₁^–1A₁₂=О откуда и получаем

А₂₂=A₂₁A₁₁^–1A_12.

□

Следствие 1. Положим матрица А=А_np ранга r и разделена на подматрицы, как в теореме П.8.2, где A₂₂ размеров rxr и ранга r. Тогда обобщенная обратная матрицы А задаётся выражением

А^–=,                                             (П.8.5)

где три нулевые матрицы О таких размеров, что А^– размеров pxn.

□

Невырожденная подматрица матрицы А необязательно должна быть в положении A₁₁ или A₂₂, как в теореме П.8.2 или её следствии. Теорема П.8.2 может быть расширена до следующего алгоритма отыскания обобщенной обратной матрицы А^– для любой матрицы А=А_np ранга r [Searle (1982) стр.218]:

1. Найти любую невырожденную подматрицу С размеров rxr. При этом необязательно чтобы элементы С занимали соседние строки и столбцы в А.
2. Найти С^–1 и затем (С^–1)^Т.
3. Заменить элементы С элементами (С^–1)^Т.
4. Заменить все другие элементы в А нулями.
5. Транспонировать полученную матрицу.
6. В результате получается А^–.

Некоторые свойства обобщённых обращений приведены в следующей теореме.

Теорема П.8.3. Пусть матрица А=А_np ранга r, А^– - любая обобщённая обратная матрицы A и (A^ТA)^– - любая обобщённая обратная матрицы A^ТA. Тогда:

1. ранг(A^–A)=ранг(AA^–)=ранг(A)=r,
2. матрица (A^–)^Т является обобщённой обратной матрицы A^Т, то есть (A^Т)^–=(A^–)^Т,
3. A=A(A^ТA)^–A^ТA и A^Т=A^ТA(A^ТA)^–A^Т,
4. матрица (A^ТA)^–A^Т является обобщённой обратной для А, то есть, A^–=(A^ТA)^–A^Т,
5. матрица A(A^ТA)^–A^Т симметричная, имеет ранг r и является инвариантной к выбору (A^ТA)^–, то есть, A(A^ТA)^–A^Т остается той же независимо от того какая используется обобщенная обратная (A^ТA)^–.

Доказательство:

1. По пункту 1 теоремы П.4 ранг(A^–A) ≤ ранг(A) и ранг(A) =ранг(AA^–A) ≤ранг(A^–A). Следовательно, ранг(A^–A)=ранг(A).

2. A^Т=(AA^–A)^Т=A^Т(A^–)^ТA^Т.

3. Пусть W=A[I–(A^ТA)^–A^ТA] и найдём произведение

W^ТW=[I–(A^ТA)^–A^ТA][A^ТA–A^ТA(A^ТA)^–A^ТA]

=[I–(A^ТA)^–A^ТA]О=О.

Тогда по пункту 4 теоремы П.2.3 имеем W=О и A=A(A^ТA)^–A^ТA.

4. По пункту 3 получаем A[(A^ТA)^–A^Т]A=A(A^ТA)^–A^ТA=A.

5. [Searle (1982) cтр.222] Покажем, что A(A^ТA)^–A^Т инвариантна к выбору (A^ТA)^–. Пусть В обобщённая обратная матрицы A^ТA возможно отличная от другой её обобщённой обратной С. По пункту 3 тогда А=АВA^ТA и А=АСA^ТA, так что АВA^ТA=АСA^ТA. Это означает АВA^Т=АСA^Т и чтобы доказать надо показать, что (АВA^ТA–АСA^ТA)(В^ТA^Т–С^ТA^Т)≡(АВA^Т–АСA^Т)(АВA^Т–АСA^Т). Левая сторона равна О, так как АВA^ТA=АСA^ТA. Тогда и правая сторона равна О и по пункту 2 теоремы П2.3 АВA^Т–АСA^Т=О. Чтобы показать симметрию, пусть S будет симметричной обобщённой обратной матрицы A^ТA. Тогда АSA^Т симметричная и АВA^Т=АSA^Т, так как АВA^Т инвариантна к (A^ТA)^–. Отсюда АВA^Т также симметричная. Чтобы показать, что ранг[A(A^ТA)^–A^Т]=r, используем пункты 1 и 4.

□

Обобщённая обратная симметричной матрицы необязательно будет симметричная. Однако верно и то, что для симметричной матрицы всегда можно найти симметричную обобщённую обратную. Здесь будем считать, что обобщённые обратные симметричных матриц симметричные.

Обобщённые обращения и системы уравнений

Обобщённые обращения могут использоваться для нахождения решения системы уравнений.

Теорема П.8.4. Если система уравнений Ах=с совместная и A^– - любая обобщённая обратная матрицы А, то решением этой системы является х=A^–с.

Доказательство: Так как AA^–A=А, то, умножая справа на х, имеем

AA^–Aх=Ах.

Заменяя в этом уравнении Ах на с, получаем

AA^–с=с.

Записывая последнее в виде A(A^–с)=с, видим, что A^–с является решением уравнения Ах=с.

□

Различные варианты матрицы A^– приводят к различным решениям системы Ах=с.

Теорема П.8.5. Если система уравнений Ах=с совместная, то все возможные её решения могут быть получены следующими двумя методами:

1. По формуле х=A^–с+(A^–A–I)h с использованием определенной A^–, при всех возможных значениях произвольного вектора h.
2. Использованием всех возможных вариантов A^– в х=A^–с, при условии с≠0.

Доказательство: [Searle (1982) стр.238]

1. Положим вектор х является решением системы Ах=с. Выберем h=–х. Тогда х=A^–с +(A^–A–I)h=A^–с–(A^–A–I)х=A^–с обращается в решение. Следовательно, соответствующим выбором h любое решение х может быть представлено в форме х. То есть все решения могут быть получены по формуле х=A^–с+(A^–A–I)h.

Доказательство пункта 2 теоремы основывается на следующей лемме.

Лемма. Для произвольного вектора h=h_q и известного ненулевого вектора с=с_p существует такая произвольная матрица Х=Х_qp, что h=Хс.

Доказательство леммы: Так как с≠0, то хотябы один его элемент с_k ненулевой. Запишем h=(h_i) и Х=(х_ij) при i=1, 2, …, q и j=1, 2, …, p. Пусть х_ij=h_i/с_k для j=k и х_ij=0 для остальных j. Тогда Хс=h и матрица Х произвольная.

□

2.    Для обобщённой обратной A^– матрицы А решением системы Ах=с является A^–с +(A^–A–I)h с произвольным вектором h. Допуская h=–Хс для произвольной матрицы Х, как в лемме, это решение становится

A^–с+(A^–A–I)h=[A^–AA^–+(I–A^–A)X+(–A^–)(AA^––I)]с=A*с

с матрицей А* данной в [Searle (1982) cтр.220], то есть любое решение может быть представлено в форме A*с.

□

Необходимое и достаточное условие чтобы система Ах=с была совместной, может быть сформулировано в терминах обобщенной обратной матрицы A [Graybill (1976) стр.36].

Теорема П.8.6. Система уравнений Ах=с имеет решение, если и только если для любой обобщенной обратной A^– матрицы А соблюдается равенство

AA^–c=c.                                                         (П.8.6)

Доказательство: Положим, что система уравнений Ах=с совместная. Тогда по теореме П.8.4 выражение х=A^–с является её решением. Умножая с=Ах слева на AA^–получаем

Рекомендуем посмотреть лекцию "12.3 Диагностика неисправностей манипуляторов".

AA^–с=AA^–Ах=Ах=с.

Обратно, пусть AA^–с=с. Умножим х=A^–с слева на А чтобы получать

Ах=AA^–с=с.

Следовательно, решение существует в виде х=A^–с.

□

Теорема П.8.6, как и теорема П.7.1, служит для выяснения, является ли система уравнений совместной.