Приложение Д Обратные матрицы

П.5. Обратные матрицы

Квадратная матрица полного ранга является невырожденной. Невырожденная матрица А имеет единственную обратную матрицу A^–1 с которой выполняются следующие равенства

АA^–1=A^–1А=I                                                (П.5.1)

Если квадратная матрица А не имеет полный ранг, то она не имеет обратной матрицы и является вырожденной. Заметим, что прямоугольные матрицы полного ранга не имеют единственных обратных. Из выражения (П.5.1) следует, что обратной матрицей для A^–1 является А, то есть,

(A^–1)^–1=A.                                                      (П.5.2)

Пример П.5. Пусть A=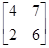, тогда A^–1= 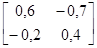и

==

□

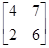
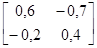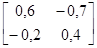
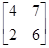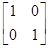
В приложениях обратные матрицы обычно находятся с использованием компьютера. Многие калькуляторы также вычисляют обратные матрицы. Алгоритмы расчета обратных небольших матриц можно найти в книгах по матричной алгебре.

Рекомендуемые материалы

Если матрица B невырожденная и AB=CB, то можно умножить обе части этого уравнения справа на B^–1 и получить A=C. (Если В вырожденная или прямоугольная, то матрицу В в AB=CB невозможно сократить с обеих сторон, см. пример П.4.2 и абзац перед примером.) Аналогично, если А невырожденная, то система уравнений Ах=с имеет единственное решение, так как обе её части можно умножить слева на A^–1 и получить

A^–1Ах=A^–1с

x=A^–1c.                                                          (П.5.3)

Два свойства обратных матриц приведены в следующих теоремах.

Теорема П.5.1. Если матрица А невырожденная, то A^Т тоже невырожденная и обратную ей матрицу можно найти из выражения

(A^Т)^–1=(A^–1)^Т                                                 (П.5.4)

Доказательство: Матрица A^Т невырожденная по определению, так как её строки являются столбцами матрицы А. Чтобы показать, что (A^Т)^–1=(A^–1)^Т, транспонируем обе части равенства AA^–1=I и получим (AA^–1)^Т=I^Т или (A^–1)^ТA^Т=I. Умножая обе части справа на (A^Т)^–1 получаем требуемый результат.

□

Теорема П.5.2. Если А и В невырожденные матрицы одинаковых размеров, то AB невырожденная и

(AB)^–1=B^–1A^–1                                               (П.5.5)

Доказательство: По пункту 2 теоремы П.4 матрица (AB)^–1 существует. Тогда

AB(AB)^–1=I,

A^–1AB(AB)^–1=A^–1,

B^–1B(AB)^–1=B^–1A^–1,

(AB)^–1=B^–1A^–1.

□

Рассмотрим теперь обратные матрицы некоторых специальных матриц. Если симметричная и невырожденная матрица А разделена на подматрицы в виде

А=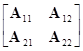

и если B=A₂₂–A₂₁A₁₁^–1A₁₂, то при условии существования A₁₁^–1 и B^–1 обратная матрицы А задается выражением

A^–1=.      (П.5.6)

В качестве применения выражения (П.5.6) найдём обратную матрицу симметричной невырожденной матрицы

А=,

где A₁₁ - квадратная матрица, a₂₂ - скаляр и a₁₂ - вектор. Если существует A₁₁^–1, то матрицу A^–1 можно представить в виде

A^–1=,                            (П.5.7)

где b=a₂₂–a₁₂^ТA₁₁^–1a₁₂.

Другим случаем применения выражения (П.5.6) является

=.                                               (П.5.8)

Если квадратная невырожденная матрица вида B+cc^Т, где с - вектор и B - невырожденная матрица, то

(B+cc^Т)^–1=B^–1–B^–1cc^ТB^–1(1+c^ТB^–1c)^–1                       (П.5.9)

[Abadir, Magnus (2005) стр.87, 248]. Это проверяется умножением. Пусть b=(1+c^ТB^–1c)^–1, тогда

(B+cc^Т)(B+cc^Т)^–1=(B+cc^Т)(B^–1–B^–1cc^ТB^–1b)

=BB^–1–BB^–1cc^ТB^–1b+cc^ТB^–1–c(c^ТB^–1c)c^ТB^–1b

=I–(b–1+bc^ТB^–1c)cc^ТB^–1

=I–(b+bc^ТB^–1c–1)cc^ТB^–1

=I,

так как квадратичная форма c^ТB^–1c является просто числом и b(1+c^ТB^–1c)=1.

В более общем виде, если матрицы A, B и А+PBQ невырожденные, то

(А+PBQ)^–1=А^–1–А^–1РB(B+BQА^–1РB)^–1BQА^–1      (П.5.10)

Это выражение также проверяется умножением

(А+PBQ)[А^–1–А^–1РB(B+BQА^–1РB)^–1BQА^–1]

=АА^–1+PBQА^–1–АА^–1РB(B+BQА^–1РB)^–1BQА^–1–PBQА^–1РB(B+BQА^–1РB)^–1BQА^–1

=I+P[I–B(B+BQА^–1РB)^–1–BQА^–1РB(B+BQА^–1РB)^–1]BQА^–1

=I+P[I–(B+BQА^–1РB)(B+BQА^–1РB)^–1]BQА^–1

=I+P[I–I]BQА^–1

=I.

П.6. Определённые матрицы

Квадратичная форма была определена выражением (П.2.25). Например, квадратичная форма 3y₁²+y₂²+2y₃²+4y₁y₂+5y₁y₃–6y₂y₃ может быть записана в виде у^ТАу, где

у= и А=.

Однако ту же квадратичную форму можно представить с симметричной матрицей получаемой из исходной А по формуле

(А+А^Т)/2=.

В общем, любая квадратичная форма у^ТАу может быть представлена в виде

у^ТАу=у^Т[(А+А^Т)/2]у.                                                           (П.6.1)

Поэтому матрица квадратичной формы всегда может быть выбрана так, чтобы быть симметричной и, следовательно, однозначно определённой.

Встречаемые в регрессии и дисперсионном анализе суммы квадратов могут быть представлены в виде квадратичной формы у^ТАу, где у - вектор результатов наблюдений. Такие квадратичные формы остаются положительными (или, по крайней мере, неотрицательными) для всех возможных значений элементов вектора у. Рассмотрим теперь квадратичные формы этого типа.

Если симметричная матрица А удовлетворяет условию у^ТАу>0 то для всех возможных у≠0 квадратичная форма у^ТАу является положительно определённой и входящая в неё матрица А тоже положительно определённая. Если же у^ТАу<0, то для всех возможных у≠0 квадратичная форма у^ТАу является отрицательно определённой и входящая в неё матрица А тоже отрицательно определённая.

Аналогично, если у^ТАу≥0 для всех у и есть по крайней мере один вектор у≠0 такой, что у^ТАу=0, то квадратичная форма у^ТАу и матрица А неотрицательно определённые. Если же у^ТАу≤0 для всех у и есть по крайней мере один вектор у≠0 такой, что у^ТАу=0, то квадратичная форма у^ТАу и матрица А неположительно определённые.

Положительно и неотрицательно определённые матрицы показаны в следующем примере.

Пример П.6. В качестве примера положительно определённой матрицы рассмотрим

А=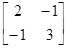

и связаную с ней квадратичную форму

у^ТАу=2у₁²–2у₁у₂+3у₂²=2(у₁–у₂/2)²+5у₂²/2,

которая явно положительна если у₁ и у₂ не равны нулю.

В качестве примера неотрицательно определённой матрицы возмём выражение

(2у₁–у₂)²+(3у₁–у₃)²+(3у₂–2у₃)²,

которое может быть представлено в виде квадратичной формы у^ТАу с матрицей

А=.

Если 2y₁=y₂, 3y₁=y₃ и 3y₂=2y₃, то (2y₁–y₂)²+(3y₁–y₃)²+(3y₂–2y₃)²=0. Таким образом, у^ТАу=0 для любого вектора у, значения элементов которого соответствуют уравнениям 2y₁=y₂, 3y₁=y₃ и 3y₂=2y₃, например, у^Т= [1, 2, 3]. В противном случае у^ТАу>0 (кроме, у=0).

□

В матрицах примера П.6 диагональные элементы положительные числа. В общем, для положительно определённых матриц это справедливо.

Теорема П.6.1.

1. Если матрица А положительно определённая, то все её диагональные элементы a_ii положительные.
2. Если матрица А неотрицательно определённая, то все a_ii ≥0.

Доказательство:

1. Пусть у^T= [0,..., 0, 1, 0,..., 0] с 1 в i-й позиции и 0 в остальных. Тогда у^ТАу=a_ii >0.
2. Пусть у^T= [0,..., 0, 1, 0,..., 0] с 1 в i-й позиции и 0 в остальных. Тогда у^ТАу=a_ii ≥0.

□

Некоторые дополнительные свойства положительно и неотрицательно определённых матриц даны в следующих теоремах.

Теорема П.6.2. Пусть Р - невырожденная матрица.

1. Если А положительно определённая, то и P^ТАР положительно определённая.
2. Если А неотрицательно определённая, то и P^ТАР неотрицательно определённая.

Доказательство:

1. Чтобы показать, что у^ТP^ТАРу >0 при у≠0, заметим, что у^Т(P^ТАР)у=(Ру)^ТA(Ру). Так как А положительно определённая, то (Ру)^ТA(Ру)>0, при условии, что Ру≠0. В силу (П.5.3), Ру=0 только если у=0, так как P^–1Py=y=0. Отсюда, если у≠0, то у^ТP^ТАРу>0.
2. Доказательство аналогично проведённому в пункте 1, где знак > необходимо заменить на ≥.

□

Следствие 1. Пусть матрицы А=A_пп положительно определённая и В=В_kп - любая матрица ранга k ≤ п. Тогда матрица BAB^Т положительно определённая.

Доказательство: Квадратичная форма у^ТBAB^Ту=(B^Ту)^ТA(B^Ту)>0, если B^Ту≠0, так как А положительно определённая. Вектор B^Ту=у₁b₁+y₂b₂+…+y_kb_k, где b₁, b₂,…, b_k – столбцы матрицы B^Т или строки матрицы В. Так как матрица В ранга k, то её строки линейно независимы и не существует такого ненулевого вектора у чтобы B^Ту=0.

□

Следствие 2. Пусть матрица А=A_рр положительно определённая и В=В_kр - любая. Если k > р или ранг(B)=r, где r <k и r <р, то матрица BAB^Т неотрицательно определённая.

Доказательство: Подобно доказательству следствия 1.

□

Теорема П.6.3. Симметричная матрица А положительно определённая, если и только если существует невырожденная матрица P такая, что А=P^ТР.

Доказательство: Докажем часть «если». Для невырожденной матрицы P пусть А=P^ТР. Тогда

у^ТАу=у^ТP^ТРу=(Ру)^Т(Ру)

это произведение вектора на себя или сумма квадратов является положительной, кроме случая Ру=0. В силу (П.5.3), равенство Ру=0 соблюдается, только если у=0.

В части «только если» докажем, что если А положительно определённая, то А=P^ТР, где Р невырожденная. По теореме П.12.4 имеем A=MLM^T, где M ортогональная и L=диаг[l₁, l₂, …, l_n] со всеми l_i>0. В силу (П.12.17) и (П.12.18), A=MLM^T=ML^1/2L^1/2M^T =(L^1/2M^T)^T(L^1/2M^T)=P^ТР, где L^1/2=(, , ..., ). Матрица L^1/2 и ортогональная матрица невырожденные, поэтому по теореме П.5.2 матрица Р=L^1/2M^T невырожденная.

□

Следствие 1. Любая положительно определённая матрица является невырожденной.

Доказательство: Это следует из теоремы П.6.3 и пункта 2 теоремы П.4.

□

Один из методов представления положительно определенной матрицы А в виде произведения P^ТР, как в теореме П.6.3, обеспечивается разложением Холецкого [Seber, Lee (2003) стр.335-337] с помощью которого можно однозначно разложить матрицу А в виде A=T^TT, где T - невырожденная верхняя треугольная матрица.

Для любой квадратной или прямоугольной матрицы B матрица B^TB положительно или неотрицательно определённая.

Теорема П.6.4. Пусть матрица В=В_nр имеет р ≤ n. Тогда:

1. Если ранг(B)=р, то матрица B^TB положительно определённая.
2. Если ранг(B) < р, то матрица B^TB неотрицательно определённая.

Доказательство:

1. Чтобы показать, что у^ТB^TBу >0 при у≠0, заметим, что

у^ТB^TBу=(Bу)^Т(Bу)

является суммой квадратов и поэтому положительна, за исключением когда Bу=0. В силу (П.3.3), Bу можно представить в виде

Bу=y₁b₁+y₂b₂+...+y_pb_p.

Эта линейная комбинация не равна 0 (для любого у≠0), так как ранг(B)=p и, следовательно, столбцы матрицы B линейно независимы.

1. Если ранг(B) < p, то можно найти такой вектор у≠0, что

Bу=y₁b₁+y₂b₂+...+y_pb_p=0,

так как столбцы матрицы B линейно зависимы [см. (П.4.1)]. Поэтому у^ТB^TBу≥0.

□

Заметим, что если матрица B квадратная, то матрица BB=B² необязательно будет неотрицательно определённой. Например, пусть

B=, тогда B²=BB= и B^TB=.

В этом случае, B² не является неотрицательно определённой, но B^TB - неотрицательно определённая, так как у^ТB^TBу=2(y₁–2y₂)².

Следствие 1. Матрица BB^T положительно определённая, если В имеет полный ранг по строкам, в противном случае матрица BB^T - неотрицательно определённая.

□

Два дополнительных свойства положительно определённых матриц даны в следующих теоремах.

Теорема П.6.5. Если матрица А положительно определённая, то и A^–1 положительно определённая.

Рекомендуем посмотреть лекцию "4.5 Период дворцовых переворотов".

Доказательство: По теореме П.6.3 имеем A=Р^TР, где Р - невырожденная матрица. С учётом теорем П.5.1 и П.5.2, получаем A^–1=(Р^TР)^–1=P^–1(Р^T)^–1=P^–1(P^–1)^T. По теореме П.6.3 эта матрица положительно определённая.

□

Теорема П.6.6. Если матрица А положительно определённая и разделена на подматрицы в виде

А=,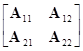

где подматрицы A₁₁ и A₂₂ квадратные, то они положительно определённые.

Доказательство: Матрицу A₁₁ можно записать, например, в виде A₁₁=[В, O]A, где В тех же размеров, что и A₁₁. Тогда по следствию 1 теоремы П.6.2, матрица A₁₁ положительно определённая.