Приложение Б Операции с матрицами

П.2. Операции с матрицами

Определим сумму и произведение матриц, а также рассмотрим некоторые их свойства.

Сумма двух матриц

Если две матрицы имеют одинаковые размеры, то с ними можно выполнить операцию сложения. Сумма матриц находится путем сложения их соответствующих элементов. Так, если А и В размеров nxр, то С=А+B - матрица тех же размеров nxр и находится в виде C=(c_ij)=(a_ij+b_ij), например,

+=.

Разность G=А–B двух матриц А и В находится в виде: G=(g_ij)=(a_ij–b_ij).

Два свойства сложения матриц приведены в следующей теореме.

Теорема П.2.1. Если матрицы А и В обе размеров nxm, то

1. A+B=B+A.                                                   (П.2.1)
2. (A+B)^Т=A^Т+B^Т.                                            (П.2.2)

Доказательство: Пункт 1 следует из коммутативности действительных чисел

Рекомендуемые материалы

a_ij+b_ij=b_ij+a_ij.

Для пункта 2 пусть С=А+В. Тогда, в силу (П.1.3),

С^Т=(с_ij)^Т=(с_ji)=(a_ji+b_ji)=(a_ji)+(b_ji)=А^Т+В^Т.

□

Произведение матрицы на число

Любая матрица может быть умножена на любое скалярное число. Произведение матрицы на скаляр с определяется, как произведение каждого элемента матрицы на этот скаляр

сА=(сa_ij)=.                         (П.2.3)

Так как ca_ij=a_ijc, то произведение скаляра и матрицы коммутативно

cA=Ac.                                                          (П.2.4)

Произведение двух матриц

Для того чтобы произведение АВ было определено необходимо чтобы число столбцов матрицы A было равно числу строк матрицы B. Тогда (ij)-й элемент произведения С=АВ находится в виде

c_ij=,                                                 (П.2.5)

что является суммой произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Таким образом, каждая строка матрицы A умножается на каждый столбец матрицы B. Если матрица A размеров nxm и матрица В размеров mxp, то матрица С=АВ получается размеров nxр. Покажем умножение матриц на следующем примере.

Пример П.2.1. Пусть А= и В=, тогда

АВ==

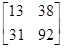
ВА==

□

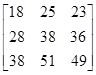
Если для матриц А=А_nm и B=В_mр имеем р≠n, то произведение АВ определено, а произведение ВА неопределенно. Для матриц А=А_nр и B=В_рn произведение AB имеет размеры nхn, а произведение ВА имеет размеры рхр. В этом случае, конечно АВ≠ВА, как показано в примере П.2.1. Если А и В обе одинаковых размеров nхn, то AB и BA имеют одинаковые размеры, но в общем

АВ≠ВА.                                                        (П.2.6)

[Есть несколько исключений из этого правила, например, две диагональные матрицы или квадратная и единичная матрицы.] Таким образом, умножение матриц не является коммутативным и некоторые знакомые операции с вещественными числами не могут быть выполнены с матрицами. Тем не менее, умножение матриц дистрибутивно для их сложения или вычитания:

А(B±C)=AB±AC,                                                    (П.2.7)

(A±B)C=AC±BC.                                                    (П.2.8)

Используя (П.2.7) и (П.2.8) можно преобразовать произведение (А–B)(C–D) следующим образом

(А–B)(C–D)=(А–B)C–(А–B)D              [в силу (П.2.7)]

=АC–BC–АD+BD               [в силу (П.2.8)].        (П.2.9)

Умножение матрицы на вектор выполняется по тем же правилам, что и умножение матриц. Положим, что матрица А=А_nр и векторы b=b_р1, с=c_р1 и d=d_n1. Тогда произведения: Ab - вектор размеров nх1, d^ТA - вектор строка размеров 1хр, b^Тс - скалярное число, bс^Т - матрица размеров рхр и cd^Т - матрица размеров рхn. Так как b^Тс - скалярное число, то оно равно с^Тb:

b^Тс=b₁с₁+b₂с₂+...+b_рс_р, с^Тb=с₁b₁+с₂b₂+...+с_рb_р, b^Тс=с^Тb.               (П.2.10)

Матрица cd^Т получается в виде

cd^Т=.                                (П.2.11)

Аналогично

b^Тb=b₁²+b₂²+...+b_р²,                                                  (П.2.12)

bb^Т=.                                 (П.2.13)

Таким образом, b^Тb - сумма квадратов и bb^Т - симметричная квадратная матрица.

Квадратный корень из суммы квадратов значений элементов вектора b размеров рх1 является расстоянием от начала координат в пространстве р измерений до точки в этом пространстве, координаты которой определены значениями элементов вектора b. Положительное значение этого квадратного корня является длиной или нормой вектора b:

Длина вектора b==.                         (П.2.14)

Если 1 - вектор единиц размеров nх1, то, в силу (П.2.12) и (П.2.13), получаем

1^Т1=n и 11^Т==E,                             (П.2.15)

где E=Е_nn - квадратная матрица размеров nхn. Если вектор а=а_n1 и матрица А=А_nр, то

а^Т1=1^Та=,                                             (П.2.16)

1^ТА= и А1=.                 (П.2.17)

Таким образом, а^Т1 - сумма элементов вектора а, 1^ТА – вектор строка сумм элементов столбцов матрицы A и A1 - вектор столбец сумм элементов строк матрицы А. Заметим, что в а^Т1 и 1^ТА вектор 1 размеров nх1, а в A1 вектор 1 размеров рх1.

Транспозиция произведения двух матриц равна произведению транспозиций сомножителей в обратном порядке.

Теорема П.2.2. Для матриц А=А_nр и В=В_рm имеем

(AB)^Т=B^ТA^Т.                                                 (П.2.18)

Доказательство дано в [Беклемишев (2006), стр.125].

□

Покажем применение теоремы П.2.2 для матриц А=А₂₃ и B=В₃₂:

AB=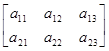

=,

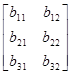
(AB)^Т=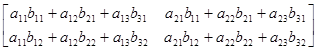

=

=

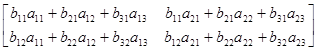
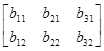
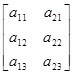
=B^ТA^Т

Если последовательно применять выражение (П.2.18) к произведению любого числа матриц, то получаем

(ABС...Z)^Т=Z^Т…C^ТB^ТA^Т.

Любая матрица А может быть умножена на свою транспозицию для образования произведений A^ТA или AA^Т. Некоторые свойства этих двух произведений приведены в следующей теореме.

Теорема П.2.3. Пусть А=А_nр - любая матрица. Тогда произведения A^ТA и AA^Т имеют следующие свойства:

1. Матрица A^ТA имеет размеры рхр и её элементы равны произведениям столбцов А.
2. Матрица AA^Т имеет размеры nхn и её элементы равны произведениям строк А.
3. Обе матрицы A^ТA и AA^Т симметричные.
4. Если A^ТA=O, то А=О.

Доказательство:

Доказательства пунктов 1 и 2 следуют из определения умножения матриц.

3. (A^ТA)^Т=A^Т(A^Т)^Т=A^ТA и (AA^Т)^Т=(A^Т)^ТA^Т=AA^Т.

4. Число а_i^Tа_i является i–м диагональным элементом матрицы A^ТA, где а_i - i-й столбец матрицы А. Так как а_i^Tа_i==0, то имеем а_i=0.

□

Положим, матрицы А=А_nm и В=В_mр. Пусть a_iс будет i-й строкой матрицы А, b_j будет j-м столбцом матрицы В и эти матрицы можно представить в виде

А= и В=[b₁, b₂, …, b_p].

Тогда, по определению, (ij)-м элементом произведения AB является a_iсb_j, то есть,

АВ=.

Результат произведения можно записать с использованием строк матрицы А:

АВ===В.                         (П.2.19)

С помощью матрицы А первый столбец произведения AB записывается в виде

Ab₁=b₁=.

Аналогично, второй столбец можно записать в виде Ab₂ и так далее. Таким образом, AB можно записать посредством столбцов матрицы B следующим образом:

АВ=А[b₁, b₂, …, b_р]=[Аb₁, Аb₂, …, Аb_р].                         (П.2.20)

Пусть матрица A=А_nn и матрица D=диаг[d₁, d₂,..., d_n]. Тогда в произведении DА элементы i-й строки матрицы А умножаются на d_i, а в произведении AD элементы j-го столбца матрицы А умножаются на d_j. Например, если n=3, то имеем

DA=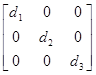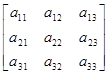=,    (П.2.21)

AD=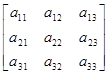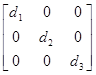=,     (П.2.22)

DAD=.                                            (П.2.23)

Обратим внимание, что DA≠AD. Тем не менее, в случае, когда диагональная матрица единичная, то (П.2.21) и (П.2.22) сводятся к выражению

IA=AI=A.                                                     (П.2.24)

Если матрица А прямоугольная, то (П.2.24) остается в силе, но единичные матрицы для умножения слева и справа должны быть соответствующих размеров. Это также справедливо и для выражений (П.2.21), (П.2.22) и (П.2.23), где диагональные матрицы также должны быть соответствующих размеров [Беклемишев (2006) стр.126].

Если А - симметричная матрица и у - вектор, то произведение

у^ТАу=+                                      (П.2.25)

называется квадратичной формой. Если векторы х=х_n1, у=у_р1 и матрица А=А_nр, то произведение

х^ТАу=                                                       (П.2.26)

называется билинейной формой.

Произведение Адамара

Обратите внимание на лекцию "Сарматы".

Иногда применяется третий тип произведения матриц, называемый поэлементным или произведением Адамара. Если две матрицы или два вектора имеют одинаковые размеры, то их произведение Адамара находится простым умножением их соответствующих элементов:

А◦В=(а_ijb_ij)=.                        (П.2.27)

Произведение Кронекера

Если матрица А имеет размеры тхn и матрица В имеет размеры pхq, то их произведение Кронекера определяется матрицей размеров тpхnq

АB=.                                      (П.2.28)

В общем случае, АB≠ВА и матрицы могут быть векторами [Seber (2008) cтр.234].