Проверка подмножества параметров
9.2. Проверка подмножества параметров
В более общем случае положим необходимо проверить гипотезу, что подмножество факторов является бесполезными для оценки ожидаемых значений переменных отклика. Простым примером является нулевая гипотеза H0: bj=0 для одного параметра bj. Если эта гипотеза H0 ложна, то член bjxj сохраняется в модели. В качестве другого примера, рассмотрим линейную модель
у=b0+b1x1+b2x2+b3x12+b4x22+b5x1x2+e,
для которой желательно проверить гипотезу H0: b3=b4=b5=0. Если эта гипотеза ложна, то постулируется модель с функцией в виде полинома второго, а не первого порядка.
Без ограничения общности будем считать, что проверяемые параметры являются элементами вектора b и для них имеются соответствующие столбцы матрицы X модели. Тогда вектор b и матрицу X можно соответствующим образом разделить и модель для всех п опытов эксперимента имеет вид
у=Xb+e=[X1, X2]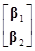 +e
+e
=X1b1+X2b2+e, (9.2.1)
где вектор b2 содержит подлежащие проверке параметры. Параметр b0 обычно является элементом вектора b1.
В рассматриваемом случае представляет интерес нулевая гипотеза H0: b2=0. Если обозначить h число параметров в векторе b2, то имеем матрицу Х2 размеров nxh, вектор b1 размеров (р–h)x1 и матрицу Х1 размеров nx(р–h). Таким образом, получаем два вектора b1T= [b0, b1,…, bр–h] и b2T= [bр–h+1, …, bр–1]. Для модели из примера с функциями в виде полиномов первого и второго порядка, пусть b1T= [b0, b1, b2] и b2T= [b3, b4, b5]. При этом отметим, что вектор b1 в (9.2.1) отличается от b1 в разделе 9.1, где вектор b был разделён в виде b= и вектор b1 содержал все параметры за исключением b0.
и вектор b1 содержал все параметры за исключением b0.
Рекомендуемые материалы
Для проверки гипотезы H0: b2=0 в сравнении с гипотезой H1: b2≠0 воспользуемся понятиями адекватной и неадекватной моделей. Адекватная модель представляется выражением (9.2.1), а если гипотеза H0: b2=0 верна, то неадекватная модель имеет вид
у=X1b1*+e*. (9.2.2)
Здесь обозначения b1* и e* используются, как и в разделе 8.2, так как, если матрицы X1 и X2 между собой неортогональны (см. теорему 8.2.1 и её следствие), то, как правило, векторы b1* и e* неадекватной модели отличаются от векторов b1 и e адекватной модели. Оценка вектора b1* делается по формуле  = (X1ТX1)–1X1Тy и, в общем, её результат отличается от результата оценки по формуле
= (X1ТX1)–1X1Тy и, в общем, её результат отличается от результата оценки по формуле  = (XТX)–1XТy первых р–h элементов вектора b модели (9.2.1). Однако, если матрицы X1 и X2 между собой ортогональны, то по теореме 8.3 результаты оценки векторов b1* и b1 получаются одинаковыми.
= (XТX)–1XТy первых р–h элементов вектора b модели (9.2.1). Однако, если матрицы X1 и X2 между собой ортогональны, то по теореме 8.3 результаты оценки векторов b1* и b1 получаются одинаковыми.
Для сравнения моделей (9.2.1) и (9.2.2) может использоваться дополнительная сумма квадратов [Box, Draper (2007) стр. 51-52]. В общем, если имеется линейная модель, включающая некоторый набор факторов со значениями в столбцах матрицы Х1, и рассматривается более разработанная модель с дополнительными факторами, значения которых представлены в столбцах матрицы Х2, то связанная с дополнительными факторами сумма квадратов, при заданных остальных, может быть найдена посредством сначала оценки параметров модели (9.2.1), а затем оценки параметров более простой модели (9.2.2). Дополнительная сумма квадратов из-за использования дополнительных факторов получается затем либо как разность между регрессионными суммами квадратов для моделей (9.2.1) и (9.2.2), либо как разность между суммами квадратов остатков для этих моделей.
Для сравнения результатов оценки параметров моделей (9.2.1) и (9.2.2) к сумме квадратов  =уТу–n
=уТу–n значений переменных отклика, скорректированной их усреднённым значением, прибавим и вычтем регрессионные суммы квадратов
значений переменных отклика, скорректированной их усреднённым значением, прибавим и вычтем регрессионные суммы квадратов  ТXТy и
ТXТy и  ТX1Тy соответственно адекватной и неадекватной моделей чтобы получить выражение
ТX1Тy соответственно адекватной и неадекватной моделей чтобы получить выражение
уТу–n = (уТу–
= (уТу– ТXТy)+(
ТXТy)+( ТXТy–
ТXТy– ТX1Тy)+(
ТX1Тy)+( ТX1Тy–n
ТX1Тy–n ) (9.2.3)
) (9.2.3)
или в обозначениях сумм
STс=SE+S(b2|b1)+SRс*(неадекватной), (9.2.4)
где S(b2|b1) = ТXТy–
ТXТy– ТX1Тy - дополнительная сумма квадратов получаемая в результате использования дополнительных факторов и их параметров, являющихся элементами вектора b2. Следует отметить, что сумма S(b2|b1) может быть выражена также в виде
ТX1Тy - дополнительная сумма квадратов получаемая в результате использования дополнительных факторов и их параметров, являющихся элементами вектора b2. Следует отметить, что сумма S(b2|b1) может быть выражена также в виде
S(b2|b1) = ТXТy–n
ТXТy–n –(
–( ТX1Тy–n
ТX1Тy–n )
)
=SRс(адекватной)–SRс*(неадекватной),
что является разностью скорректированных усреднённым значением переменных отклика регрессионных сумм квадратов адекватной и неадекватной моделей.
Если гипотеза H0: b2=0 верна, то ожидается, что S(b2|b1) будет малой и STс в (9.2.4) состоит в основном из SE и SRс*(неадекватной). Если b2≠0, то S(b2|b1) будет большой и на неё приходится больше от суммы STс. Таким образом, для адекватной модели проверяется гипотеза H0: b2=0, где нет ограничений по b1. Вектор b1 не игнорируется, полагая b1=0, а проверяется гипотеза H0: b2=0 в присутствии b1, то есть, свыше того, что b1 вносит в STс.
Для получения статистики проверки гипотезы на основе суммы S(b2|b1) сначала запишем выражение (9.2.3) в виде квадратичных форм относительно вектора у. Используя формулы  =(XТX)–1XТy,
=(XТX)–1XТy,  =(X1ТX1)–1X1Тy и (5.1.2), выражение (9.2.3) преобразуется к виду
=(X1ТX1)–1X1Тy и (5.1.2), выражение (9.2.3) преобразуется к виду
yT(I–Е/n)y=уТу–уТX(XТX)–1XТу+уТX(XТX)–1XТу–уТX1(X1ТX1)–1X1Тy
+уТX1(X1ТX1)–1X1Тy–уТЕ/nу
=yT[I–X(XТX)–1XТ]y+yT[X(XТX)–1XТ–X1(X1ТX1)–1X1Т]у
+yT[X1(X1ТX1)–1X1Т–Е/n]y (9.2.5)
=yT(I–H)у+yT(H–H1)у+yT(H1–Е/n)y, (9.2.6)
где H=X(XТX)–1XТ и H1=X1(X1ТX1)–1X1Т. По пункту 1 теоремы П.13.5 матрица I–H идемпотентная и имеет ранг п–р, где р – ранг матрицы X (р является также числом элементов вектора b). В следующей теореме показано, что и матрица H–H1 является идемпотентной.
Теорема 9.2.1. Матрица H–H1=X(XТX)–1XТ–X1(X1ТX1)–1X1Т идемпотентная и имеет ранг h, являющийся числом элементов вектора b2.
Доказательство: Умножая X слева на Н, получаем
HX=X(XТX)–1XТX=X
или
X= [X(XТX)–1XТ]X. (9.2.7)
Разделение матрицы X=[X1, X2] в левой части равенства (9.2.7) и последней матрицы X в правой его части даёт путем умножения по формуле (П.2.20) выражение
[X1, X2]= [X(XТX)–1XТ][X1, X2]
= [X(XТX)–1XТX1, X(XТX)–1XТX2].
Из него получаем
X1=X(XТX)–1XТX1 и X2=X(XТX)–1XТX2. (9.2.8)
C использованием полученных в (9.2.8) выражений для X1 и X2, а также их транспозиций, произведения матриц HH1 и H1H сводятся к следующим результатам:
HH1=H1 и H1H=H1. (9.2.9)
Матрицы H и H1 идемпотентные, следовательно, и матрица H–H1 также идемпотентная
(H–H1)(H–H1)=HH–H1H–HH1+H1H1
=H–H1–H1+H1
=H–H1.
Для нахождения ранга матрицы H–H1 по теореме П.13.4 имеем
ранг(H–H1)=след(H–H1)
=след(H)–след(H1) [в силу (П.11.1)]
=след[X(XТX)–1XТ]–след[X1(X1ТX1)–1X1Т]
=след[XТX(XТX)–1]–след[X1ТX1(X1ТX1)–1] [в силу (П.11.2)]
=след(Iр)–след(Iр–h)=р–(р–h)
=h.
□
Найдем теперь распределения квадратичных форм yT(I–H)у и yT(H–H1)у в выражении (9.2.6) и покажем, что они независимы.
Теорема 9.2.2. Если вектор у имеет нормальное распределение Nn(Xb, s2I) и матрицы H=X(XТX)–1XТ и H1=X1(X1ТX1)–1X1Т, то
- Квадратичная форма yT(I–H)у/s2 имеет центральное распределение c2(п–р),
- Квадратичная форма yT(H–H1)у/s2 имеет нецентральное распределение c2(h, g1) с параметром нецентральности g1=b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/(2s2).
- Квадратичные формы yT(I–H)у и yT(H–H1)у статистически независимы.
Доказательство: Прибавляя квадратичную форму yT(Е/n)y к обеим сторонам выражения (9.2.6) получаем выражение yTy=yT(I–H)у+yT(H–H1)у+yTH1y. В теореме 9.2.1 доказано, что вместе с матрицами I–H и H1 матрица H–H1 тоже идемпотентная. Поэтому все пункты данной теоремы доказываются на основе следствия 1 теоремы 5.6.3.
Параметр нецентральности g1 получается следующим образом. Его числитель
yTAiy=bTXT(H–H1)Xb
=bTXTX(XТX)–1XТXb–bTXTX1(X1ТX1)–1X1ТXb
=bTXTXb–bTXTX1(X1ТX1)–1X1ТXb
=[b1Т, b2Т] [X1, X2]
[X1, X2]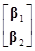 –[b1Т, b2Т]
–[b1Т, b2Т] X1(X1ТX1)–1X1Т[X1, X2]
X1(X1ТX1)–1X1Т[X1, X2]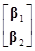
=(b1ТX1Т+b2ТX2Т)(X1b1+X2b2) –(b1ТX1Т+b2ТX2Т)X1(X1ТX1)–1X1Т(X1b1+X2b2)
=b1ТX1ТX1b1+b2ТX2ТX1b1+b1ТX1ТX2b2+b2ТX2ТX2b2–b1ТX1ТX1b1–b2ТX2ТX1b1
–b1ТX1ТX2b2–b2ТX2ТX1(X1ТX1)–1X1ТX2b2
=b2ТX2ТX2b2–b2ТX2ТX1(X1ТX1)–1X1ТX2b2
=b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2]b2.
Следовательно, g1=yTAiy/(2s2)=b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/(2s2).
□
Если в пункте 2 теоремы 9.2.2 параметр не центральности g1=0, то квадратичная форма yT(H–H1)у/s2 принимает центральное распределение c2(h). При этом g1=0, если и только если b2=0, так как матрица X2ТX2–X2ТX1(X1ТX1)–1X1ТX2 положительно определённая. Это доказывается следующим образом. Обозначим произведение XТX матрицей G. Тогда, пользуясь разделением матрицы X=[X1, X2], имеем
G=XТX= [X1, X2]=
[X1, X2]= =
= .
.
Если обозначить четыре соответствующих блока матрицы G–1 как Gij, то в силу (П.5.4), G22=(G22–G21G11–1G12)–1. По теореме П.6.5 матрица G–1 положительно определённая, по теореме П.6.6 матрица G22 положительно определённая и по теореме П.6.5 матрица (G22)–1 =G22–G21G11–1G12=X2ТX2–X2ТX1(X1ТX1)–1X1ТX2 является положительно определённой.
Проверка гипотезы H0: b2=0 в сравнении с гипотезой H1: b2≠0 на основе статистики FH даётся в следующей теореме.
Теорема 9.2.3. Пусть вектор у имеет нормальное распределение Nn(Xb, s2I) и статистика FH определяется следующим образом
FH= =
= (9.2.10)
(9.2.10)
= , (9.2.11)
, (9.2.11)
где для адекватной модели у=Xb+e вектор оценки  =(XТX)–1XТy и для неадекватной модели у=X1b1*+e* вектор оценки
=(XТX)–1XТy и для неадекватной модели у=X1b1*+e* вектор оценки  = (X1ТX1)–1X1Тy, то распределения статистики FH получаются следующими:
= (X1ТX1)–1X1Тy, то распределения статистики FH получаются следующими:
- Если гипотеза H0: b2=0 ложна, то статистика FH принимает нецентральное распределение F(h, п–р, g1) с параметром не центральности
g1=b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/(2s2).
- Если гипотеза H0: b2=0 верна, то g1=0 и статистика FH приобретает центральное распределение F(h, п–p).
Доказательство:
- Этот пункт доказывается на основе (5.4.3) и по теореме 9.2.2.
- Этот пункт доказывается на основе (5.4.1) и по теореме 9.2.2.
□
Проверка нулевой гипотезы H0: b2=0 проводится следующим образом. Эта гипотеза ложна, если значение статистики FH больше критического значения Fкр случайной переменной, имеющей центральное распределение F(h, п–р), для выбранной равной 1–α интегральной вероятности на интервале от 0 до Fкр. Гипотеза H0: b2=0 также ложна, если пи-значение статистики FH меньше α. Так как матрица X2ТX2–X2ТX1(X1ТX1)–1X1ТX2 положительно определённая и, если гипотеза H0: b2=0 ложна, то g1>0. Это ведёт к тому, что гипотеза H0: b2=0 становится ложной при больших значениях FH.
Формулы расчётов для проверки нулевой гипотезы на основе статистики FH сведены в таблицу 9.2.1 дисперсионного анализа.
Таблица 9.2.1. Дисперсионный анализ проверки гипотезы H0: b2=0
| Источники дисперсии | Степени свободы | Суммы квадратов | Средние квадратичные | Статистика проверки FH |
| Из-за b2 | h | S(b2|b1)= | S(b2|b1)/h |
|
| Остатки | п–р | SE=уТу– | SE/(п–р) | |
| Итого | п–1 | SТ=уТу–n |
Выше установлено, что математическое ожидание Е[SE/(п–р)]=s2. По пункту 2 теоремы 9.2.2 величина S(b2|b1)/s2 имеет нецентральное распределение c2(h, g1) с параметром не центральности g1=b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/(2s2). Тогда, в силу (5.3.6), E[S(b2|b1)/s2]=h+2g1 и E[S(b2|b1)/h]=s2+b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/h. Если гипотеза H0: b2=0 верна, то оба ожидаемых средних квадратичных в таблице 9.2.1 равны s2, а если H0: b2=0 ложна, то математическое ожидание E[S(b2|b1)/h] будет больше математического ожидания E[SE/(п–р)], так как матрица X2ТX2–X2ТX1(X1ТX1)–1X1ТX2 положительно определённая. Поэтому при больших значениях FH гипотеза H0: b2=0 становится ложной.
Пример 9.2.1. Рассмотрим полученную в примере 8.2.1 модель для данных из таблицы 8.2. Для проверки полезности члена второго порядка при оценке переменной отклика в качестве адекватной модели используется модель с полиномиальной функцией второго порядка
y2=b0+b1x+b11x2+e
и проверяется гипотеза H0: b11=0. Для этой адекватной модели скорректированная усреднённым регрессионная сумма квадратов  ТXТy–n
ТXТy–n =851,863, а для неадекватной модели y2=b0*+b1*x+e* скорректированная усреднённым регрессионная сумма квадратов
=851,863, а для неадекватной модели y2=b0*+b1*x+e* скорректированная усреднённым регрессионная сумма квадратов  ТX1Тy–n
ТX1Тy–n =195,783. Их разность
=195,783. Их разность  ТXТy–
ТXТy– ТX1Тy=656,081. Сумма квадратов остатков SE=4,129 и для проверки гипотезы рассчитанная по формуле (9.2.10) статистика
ТX1Тy=656,081. Сумма квадратов остатков SE=4,129 и для проверки гипотезы рассчитанная по формуле (9.2.10) статистика
FН=656,081х2/4,129=317,83.
Значение этой статистики значительно больше критического значения Fкр=18,51 случайной переменной, имеющей распределение F(1, 2) и выбранную интегральную вероятность 1–α=0,95. Поэтому гипотеза H0: b11=0 ложна. Кроме этого, пи-значение статистики FН равно 0,003, что значительно меньше 0,05 и также указывает на ложность гипотезы H0: b11=0. Таким образом, член второго порядка необходим для оценки ожидаемого значения переменной отклика.
□
В следующей теореме рассмотрим сумму S(b2|b1) в виде квадратичной формы относительно вектора  .
.
Теорема 9.2.4. Если функция модели разделяется, как показано в (9.2.1), то сумму S(b2|b1) = ТXТy–
ТXТy– ТX1Тy можно записать в виде квадратичной формы
ТX1Тy можно записать в виде квадратичной формы
S(b2|b1) = Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2]
Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] , (9.2.12)
, (9.2.12)
где  получается при разделении вектора
получается при разделении вектора  оценки параметров адекватной модели
оценки параметров адекватной модели
 =
= = (XТX)–1XТy. (9.2.13)
= (XТX)–1XТy. (9.2.13)
Доказательство: Используя векторы  и
и  запишем произведение X
запишем произведение X в виде X
в виде X =[X1, X2]
=[X1, X2] =X1
=X1 +X2
+X2 . Чтобы представить вектор
. Чтобы представить вектор  с использованием
с использованием  и
и  , заметим, что, в силу (8.2.4), его математическое ожидание Е(
, заметим, что, в силу (8.2.4), его математическое ожидание Е( )=b1+Аb2, где матрица смещения А=(X1ТX1)–1X1ТX2 определена в теореме 8.2.1. Оценка математического ожидания Е(
)=b1+Аb2, где матрица смещения А=(X1ТX1)–1X1ТX2 определена в теореме 8.2.1. Оценка математического ожидания Е( ) может быть сделана в виде
) может быть сделана в виде  (
( )=
)= =
= +A
+A , где
, где  и
и  - векторы оценки параметров адекватной модели в соответствии с показанным в (9.2.13) разделением. Далее сумму S(b2|b1) из таблицы 9.2.1 можно записать в виде
- векторы оценки параметров адекватной модели в соответствии с показанным в (9.2.13) разделением. Далее сумму S(b2|b1) из таблицы 9.2.1 можно записать в виде
S(b2|b1) = ТXТy–
ТXТy– ТX1Тy
ТX1Тy
= ТXТX
ТXТX –
– ТX1ТX1
ТX1ТX1 [в силу нормальных уравнений]
[в силу нормальных уравнений]
= ( ТX1Т+
ТX1Т+ ТX2Т)(X1Т
ТX2Т)(X1Т +X2
+X2 )–(
)–( Т+
Т+ ТАТ)X1ТX1(
ТАТ)X1ТX1( +А
+А ).
).
Выполняя операции умножения и подставляя (X1ТX1)–1X1ТX2 вместо А, получаем (9.2.12).
□
Из выражения (9.2.12) очевидно, что сумма S(b2|b1) появляется из-за присутствия вектора b2. Из него также видно прямое соответствие между S(b2|b1) и параметром g1 нецентральности в пункте 2 теоремы 9.2.2 или ожидаемым средним квадратичным E[S(b2|b1)/h]=s2+b2Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2] b2/h.
Пример 9.2.2. Данную в таблице 9.2.1 процедуру проверки гипотезы H0: b2=0 при рассмотрении адекватной и неадекватной моделей можно использовать для проверки значимости одного параметра bj. Для этого необходимо проверить гипотезу H0: bр–1=0 и вектор b разделить в виде
b= =
= .
.
Тогда матрица X разделяется так X=[Х1, хр–1], где хр–1 - последний столбец матрицы X и матрица X1 содержит все столбцы матрицы Х, кроме столбца хр–1. Неадекватной моделью является у=X1b1*+e* и оценка вектора b1* находится по формуле  =(X1ТX1)–1X1Тy. В этом случае h=1 и статистика FН по формуле (9.2.11)
=(X1ТX1)–1X1Тy. В этом случае h=1 и статистика FН по формуле (9.2.11)
FН = . (9.2.14)
. (9.2.14)
Если гипотеза H0: bр–1=0 верна, то статистика FН имеет распределение F(1, п–р).
□
Пример 9.2.3. Рассмотренная в разделе 9.1 проверка значимости факторов модели на основе гипотезы о параметрах может быть получена на основе рассмотрения адекватной и неадекватной моделей. В этом случае матрица X и вектор b разделяются соответственно следующим образом:
Ещё посмотрите лекцию "10 Корреляционный анализ" по этой теме.
Х= [1, X1] и b= =
= .
.
Неадекватной является модель у=1b0*+e* и оценка её параметра b0* находится по формуле
 =(1Т1)–11Ту=1Ту/п=
=(1Т1)–11Ту=1Ту/п=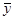 , (9.2.15)
, (9.2.15)
а регрессионная сумма квадратов находится из выражения
S(b0*)= 1Ту=
1Ту=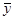
 =n
=n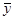 2. (9.2.16)
2. (9.2.16)
Отсюда сумма квадратов S(b1|b0) = ТXТy–n
ТXТy–n , как и в выражении (9.1.7).
, как и в выражении (9.1.7).























