Проверка значимости факторов модели и её мощность
Глава 9 Проверка гипотез и доверительные интервалы
В этой главе рассматривается проверка гипотез и доверительные интервалы параметров b0, b1, …, bр–1 модели у=Xb+e с нормированными факторами. Анализируются также доверительные интервалы и интервалы предсказания переменной отклика. Во всей главе считается, что вектор у имеет распределение Nn(Xb, s2I), а матрица X модели размеров nxр и ранга р<п.
9.1. Проверка значимости факторов модели и её мощность
В разделе 8.2 установлено, что разработка адекватной модели заключается в поиске минимально допустимого набора используемых в ней значимых факторов и параметров. Проверка гипотез является формальным методом отбора значимых факторов для модели. При этом считается, что если нулевая гипотеза H0 верна, то ни один из выбранных факторов в функции модели не оказывает влияние на переменные отклика, а если эта гипотеза ложна, то, по крайней мере, один из факторов в функции модели оказывает влияние на переменные отклика.
Чтобы продемонстрировать этот метод начнём с проверки нулевой гипотезы H0 о параметрах модели, то есть проверки того, что ни один из факторов не оказывает влияние на переменные отклика эксперимента. Эта гипотеза может быть представлена в виде H0: b1=0, где b1Т=[b1, b2, …, bр–1], и, если она верна, то ни один из контролируемых факторов эксперимента не оказывает влияние на переменные отклика. Обратим внимание, что надо проверять гипотезу H0: b1=0, а не гипотезу H0: b=0, где b= . Поскольку параметр b0 обычно неравен нулю, то нет смысла включать b0=0 в эту гипотезу. Гипотеза H0: b=0 может быть ложна исключительно из-за неравенства нулю параметра b0 и в этом случае невозможно узнать о влиянии контролируемых факторов на переменные отклика.
. Поскольку параметр b0 обычно неравен нулю, то нет смысла включать b0=0 в эту гипотезу. Гипотеза H0: b=0 может быть ложна исключительно из-за неравенства нулю параметра b0 и в этом случае невозможно узнать о влиянии контролируемых факторов на переменные отклика.
Проверка гипотезы H0: b=0 рассмотрена в разделе 6.3. Там предложена статистика проверки гипотез о параметрах модели. Если нулевая гипотеза H0 верна, то эта статистика приобретает центральное распределение F, а если гипотеза H0 ложна, то нецентральное распределение F. Метод расчёта статистики для проверки гипотез несколько упрощается, если воспользоваться моделью (7.5.26) с нормированными факторами
у=[1, X1] +e,
+e,
где X1 – матрица нормированных значений факторов, содержащая все столбцы матрицы X кроме первого. Скорректированная усреднённым переменных отклика сумма квадратов их значений STс= может быть разделена в виде
может быть разделена в виде
STс= ТX1Тy+[
ТX1Тy+[ –
– ТX1Тy]
ТX1Тy]
Рекомендуемые материалы
= ТX1Тy+SE [в силу (7.5.35)]
ТX1Тy+SE [в силу (7.5.35)]
=SRс+SE. (9.1.1)
где SRс= ТX1Тy - сумма квадратов полученная в результате регрессии и скорректированная усреднённым переменных отклика. В разделе 6.3 показано, что эту сумму квадратов можно записать в виде
ТX1Тy - сумма квадратов полученная в результате регрессии и скорректированная усреднённым переменных отклика. В разделе 6.3 показано, что эту сумму квадратов можно записать в виде
SRс=yТ[X(XТX)–1XТ–11Т/n]y.
В силу (7.5.29), это выражение преобразуется следующим образом
SRс=yТ{[1, X1]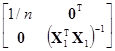
 –11Т/n}y
–11Т/n}y
=yТ[11Т/n+X1(X1ТX1)–1X1Т–11Т/n]y
=yТX1(X1ТX1)–1X1Тy,
что, при  Т=yТX1(X1ТX1)–1, приводит к SRс=
Т=yТX1(X1ТX1)–1, приводит к SRс= ТX1Тy. Матрица X(XТX)–1XТ–11Т/n является идемпотентной и имеет ранг р–1.
ТX1Тy. Матрица X(XТX)–1XТ–11Т/n является идемпотентной и имеет ранг р–1.
Формулу (7.5.31) можно преобразовать в выражение X1ТX1 =X1Тy и умножение его слева на
=X1Тy и умножение его слева на  Т даёт
Т даёт  ТX1Тy=
ТX1Тy= ТX1ТX1
ТX1ТX1 . Отсюда сумму квадратов SRс=
. Отсюда сумму квадратов SRс= ТX1Тy можно записать в виде
ТX1Тy можно записать в виде
SRс= ТX1ТX1
ТX1ТX1
=(X1 )Т(X1
)Т(X1 ). (9.1.2)
). (9.1.2)
Эта сумма квадратов зависит от вектора  оценки параметров.
оценки параметров.
Для разработки процедуры проверки гипотез на основе имющей распределение F статистики представим и остальные суммы квадратов выражения (9.1.1) в виде квадратичных форм относительно вектора у. Это необходимо для того чтобы, используя теоремы главы 5, показать, что суммы SRс и SE имеют распределения хи-квадрат и статистически независимы. Вследствие того, что сумма 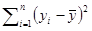
=yТ(I–Е/n)y и SE= –
– ТX1Тy, выражение (9.1.1) можно записать так
ТX1Тy, выражение (9.1.1) можно записать так
yТ(I–Е/n)y=SRс+SE
=yТX1(X1ТX1)–1X1Тy+yТ(I–Е/n)y–yТX1(X1ТX1)–1X1Тy
=yТH1y+yТ(I–Е/n–H1)y, (9.1.3)
где H1=X1(X1ТX1)–1X1Т.
В приведённой ниже теореме устанавливаются некоторые свойства трех матриц квадратичных форм выражения (9.1.3).
Теорема 9.1.1. Матрицы I–Е/n, H1=X1(X1ТX1)–1X1Т и I–Е/n–H1 обладают следующими свойствами:
1. Произведение H1(I–Е/n)=H1, (9.1.4)
2. Матрица H1 идемпотентная и её ранг равен р–1,
3. Матрица I–Е/n–H1 идемпотентная и её ранг равен п–р,
4. Произведение H1[I–Е/n–H1]=О. (9.1.5)
Доказательство:
1. В силу (7.5.27) и так как матрица I–Е/n идемпотентная, то имеем
X1Т(I–Е/n)=X1ТDs–1(I–Е/n)(I–Е/n)=X1ТDs–1(I–Е/n)=X1Т.
Следовательно, H1[I–Е/n]=X1(X1ТX1)–1X1Т[I–Е/n]=X1(X1ТX1)–1X1Т=H1.
2. Найдём произведение матриц
H1H1=X1(X1ТX1)–1X1ТX1(X1ТX1)–1X1Т=X1(X1ТX1)–1X1Т=H1.
Так как матрица H1 идемпотентная, то по теореме П.13.4 имеем ранг(H1)=след(H1). Матрица X1 размеров пх(р–1) и ранга р–1. Следовательно, и матрица H1 имеет ранг равный р–1.
3. С учётом пунктов 1 и 2 выполним умножение матрицы I–Е/n–H1 на саму себя
(I–Е/n–H1)(I–Е/n–H1)=(I–Е/n)(I–Е/n)–(I–Е/n)H1–H1(I–Е/n)+H1H1
=I–Е/n–H1.
Затем находим ранг(I–Е/n–H1)=след(I–Е/n–H1)=п–1–р+1=п–р.
4. С учётом пунктов 1 и 2 находим произведение
H1(I–Е/n–H1)=H1(I–Е/n)–H1H1=H1–H1=О.
□
Законы распределения величин SRс/s2 и SE/s2 даны в следующей теореме.
Теорема 9.1.2. Если вектор у имеет нормальное распределение Nn(Xb, s2I), то величины SRс/s2= ТX1ТX1
ТX1ТX1 /s2 и SE/s2=[
/s2 и SE/s2=[ –
– ТX1ТX1
ТX1ТX1 ]/s2 имеют следующие распределения:
]/s2 имеют следующие распределения:
- SRс/s2 имеет нецентральное распределение c2(р–1, g1) с параметром не центральности g1=yTAy/(2s2)= b1ТX1ТX1b1/(2s2).
- SE/s2 имеет центральное распределение c2(п–р).
Доказательство:
- В силу (9.1.2), SRс=
![]() ТX1ТX1
ТX1ТX1![]() =yТX1(X1ТX1)–1X1Тy, где матрица X1(X1ТX1)–1X1Т=H1 идемпотентная и ранга р–1. Поэтому по следствию 2 теоремы 5.5 величина SRс/s2 имеет нецентральное распределение c2(р–1, g1) с параметром не центральности g1=yTAy/(2s2)= b1ТX1ТX1b1/(2s2).
=yТX1(X1ТX1)–1X1Тy, где матрица X1(X1ТX1)–1X1Т=H1 идемпотентная и ранга р–1. Поэтому по следствию 2 теоремы 5.5 величина SRс/s2 имеет нецентральное распределение c2(р–1, g1) с параметром не центральности g1=yTAy/(2s2)= b1ТX1ТX1b1/(2s2). - В силу (9.1.3), SE=yТ(I–Е/n–H1)y, где матрица I–Е/n–H1 идемпотентная и ранга п–р. Поэтому по следствию 2 теоремы 5.5 величина SЕ/s2 имеет нецентральное распределение c2(п–р, g1) с параметром не центральности
g1=yTAy/(2s2)= b1ТX1Т(I–Е/n–H1)Х1b1/(2s2).
В нём по пункту 1 теоремы 9.1.1 имеем b1ТX1Т(I–Е/n)Х1b1=b1ТX1ТХ1b1 и, в силу (8.4.3), b1ТX1ТH1Х1b1=b1ТX1ТХ1b1. Следовательно, параметр не центральности g1=0 и SE/s2 обретает центральное распределение c2(п–р).
□
Условие независимости SRc и SE приведено в следующей теореме.
Теорема 9.1.3. Если вектор у имеет нормальное распределение Nn(Xb, s2I), то квадратичные формы SRc=yТH1y и SE=yТ(I–Е/n–H1)y статистически независимы.
Доказательство следует из пункта 4 теоремы 9.1.1 и следствия 1 теоремы 5.6.2.
□
Теперь на основе имеющей распределение F статистики можно создать процедуру проверки нулевой гипотезы H0: b1=0 в сравнении с альтернативной гипотезой H1: b1≠0.
Теорема 9.1.4. Если вектор у имеет нормальное распределение Nn(Xb, s2I), то в зависимости от того, что гипотеза H0: b1=0 верна или ложна, статистика
FRc= =
= (9.1.6)
(9.1.6)
приобретает следующие распределения:
1. Если гипотеза H0: b1=0 ложна, то статистика FRc обретает нецентральное распределение F(р–1, п–р, g1) с параметр не центральности g1=b1ТX1ТX1b1/(2s2).
2. Если гипотеза H0: b1=0 верна, то параметр g1=0 и статистика FRc принимает центральное распределение F(р–1, п–р).
Доказательство:
- Этот пункт доказывается на основе (5.4.3), а также теорем 9.1.2 и 9.1.3.
- Этот пункт доказывается на основе (5.4.1), а также теорем 9.1.2 и 9.1.3.
□
Обратим внимание, что параметр не центральности g1 равен нулю, если и только если b1=0, так как матрица X1ТX1 положительно определённая (см. следствие 1 теоремы П.6.2).
Проверка гипотезы H0: b1=0 осуществляется следующим образом. Эта гипотеза ложна, если значение статистики FRc больше критического значения Fкp случайной переменной, имеющей центральное распределение F(p–1, п–p), и на интервале от 0 до Fкp интегральная вероятность выбрана равной 1–α.
Для проверки гипотезы H0: b1=0 используют также пи-значение (пи – латинская буква р) статистики FRc. Это значение равно площади хвостовой части центрального распределения F(p–1, п–p) за расчетным значением статистики FRc. Если пи-значение статистики FRc меньше α, то это эквивалентно тому, что значение статистики FRc больше критического значения Fкp.
Как таблицы 6.3.1 и 6.3.2 дисперсионного анализа, так и таблица 9.1.1 представляют необходимую информацию для проверки гипотезы о значимости регрессии на основе статистики FRc. Средние квадратичные являются суммами квадратов, делёнными на степени свободы соответствующих распределений c2.
Таблица 9.1.1. Дисперсионный анализ проверки гипотезы H0: b1=0 по статистике FRc
| Источники дисперсии | Суммы квадратов | Степени свободы | Средние квадратичные | Статистика проверки FRc |
| Регрессия | SRс= | р–1 | SRс/(p–1) |
|
| Остатки | SE= | п–р | SE/(п–p) | |
| Итого | STс= | п–1 |
Для средних квадратичных из таблицы 9.1.1 можно найти их математические ожидания E[SRс/(p–1)] и Е[SE/(п–р)]. Первое из них находится по теореме 5.2.1 в виде E[SRс/(p–1)]=s2+b1ТX1ТX1b1/(p–1), а второе установлено теоремой 7.3.2 и получается Е[SE/(п–р)]=s2. Если гипотеза H0: b1=0 верна, то оба математических ожидания средних квадратичных равны s2 и их отношение равно единице. Если b1≠0, то E[SRс/(p–1)]>s2, так как матрица X1ТX1 положительно определённая, и в этом случае это отношение больше 1. Поэтому и при больших значениях статистики FRc нулевая гипотеза H0 может быть ложна.
В таблице 9.1.1 проверка гипотезы H0: b1=0 представлена для модели у=Xb+e с нормированными факторами. Можно найти суммы SRс и SE также для модели у=Xq+e с исходными значениями факторов по формулам
SRс= ТXТy–n
ТXТy–n и SE=yТy–
и SE=yТy– ТXТy. (9.1.7)
ТXТy. (9.1.7)
Однако результаты расчётов по этим формулам получаются теми же, что и по формулам
SRс= ТX1Тy и SE=
ТX1Тy и SE= –
– ТX1Тy (9.1.8)
ТX1Тy (9.1.8)
[см. (7.3.8), (7.5.24), (7.5.35)].
Пример 9.1. Используя данные таблицы примера 7.1, проверим гипотезу H0: b1=0, где b1Т= [b1, b2]. Для расчёта имеющей распределение F статистики найдём суммы SRс и SE по формулам (9.1.7). Результаты расчёта дают SRс=4,350x105 и SE=2,304x105. Такие же результаты получаются и по формулам (9.1.8), если использовать данные в таблице 8.3.3 нормированные значения факторов или нормированные значения факторов после ортогонализация столбцов матрицы модели. Результаты промежуточных расчётов по формулам таблицы 9.1.1 и расчёт статистики FRс приведены в таблице 9.1.2.
Таблица 9.1.2. Дисперсионный анализ значимости регрессии для данных примера 7.1
| Источники дисперсии | Суммы квадратов | Степени свободы | Средние квадратичные | Статистика проверки FRс |
| Вследствие b1 | SRс=4,350x105 | р–1=2 | SRс/(p–1)=2,175x105 | SRс(п–p)/[SE(p–1)] =10,387 |
| Остатки | SE=2,304x105 | п–р=11 | SE/(п–p)=2,094x104 | |
| Итого | STс=6,654x105 | п–1=13 |
Проверка гипотезы H0: b1=0 по статистике FRс показывает, что полученное значение статистики FRс=10,387 больше критического значения Fкр=3,982 случайной переменной, имеющей центральное распределение F(2, 11) и интегральную вероятность равную 0,95 на интервале от 0 до 3,982. Поэтому гипотеза H0: b1=0 ложна и делаем вывод, что, по крайней мере, один из параметров b1 или b2 не равен нулю.
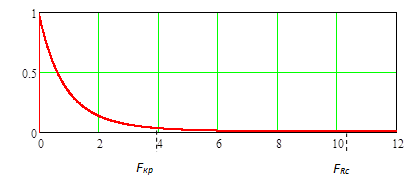
Для проверки гипотезы с использованием пи-значения на Рис 9.1 показана функция плотности вероятности центрального распределения F(2, 11), а также значение Fкр=3,982 и значение статистики FRс=10,387. Для этого распределения на интервале от 0 до значения Fкр интегральная вероятность равна 0,95, а пи-значение для Fкр равно 1–0,95=0,05. Для этого же распределения на интервале от 0 до значения FRс интегральная вероятность равна 0,997, а пи-значение для статистики FRс равно 1–0,997=0,003. Полученное пи-значение для FRс значительно меньше пи-значения для Fкр, следовательно, в результате сравнения пи-значений гипотеза H0: b1=0 также ложна.
Рекомендация для Вас - 6.1 Методы поиска решений.
Рис. 9.1. График функции плотности вероятности распределения F со степенями свободы 2 и 11.
□
Статистика FRc с распределением F используется для проверки нулевой гипотезы H0 и, если эта гипотеза верна, то распределение статистики FRc получается центральным, а если гипотеза ложна, то - нецентральным. Поэтому нецентральное распределение F часто может быть использовано для оценки мощности критерия проверки по статистике FRc [Rencher, Schaalje (2008) стр.115]. Мощность критерия определяется вероятностью отклонить гипотезу H0 для данного значения g1. Если Fкр является критическим значением случайной переменной, имеющей центральное распределение F, при выбранном значении 1–α интегральной вероятности, то мощность P(p–1, п–р, 1–α, g1) проверки может быть определена равенством
P(p–1, п–р, 1–α, g1)=Pr(w*≥Fкр), (9.1.9)
где w* - случайная переменная, имеющая нецентральное распределение F, как определено выражением (5.4.3), а Pr(w* ≥ Fкр) - вероятность того, что w*≥ Fкр. Мощность P(p–1, п–р, 1–α, g1) увеличивается, если увеличиваются п–р или 1–α, или g1, но, если увеличивается р–1, то P(p–1, п–р, 1–α, g1) уменьшается [Ghosh (1973)].
Определённую выражением (9.1.9) мощность можно найти по таблицам [Tiku (1967)] или вычислить с использованием функции плотности вероятности нецентрального распределения F. Например, в программе Mathcad можно проинтегрировать данную в разделе 5.4 функцию плотности вероятности нецентрального распределения F на интервале от 0 до Fкр и вычесть из 1. В результате получается P(p–1, п–р, 1–α, g1).




















