Оценка параметров модели

7.2. Оценка параметров модели

Модель (7.1.1) со многими факторами является множественной линейной регрессионной моделью. Как отмечалось в разделе 2.6, влияющие на отклик переменные сами могут быть функциями других переменных. Однако с любыми влияющими на отклик переменными модель остаётся линейной, если она линейна относительно её параметров.

Оценка методом наименьших квадратов

Оценка параметров модели (7.1.3) осуществляется методом наименьших квадратов по представленным в плане эксперимента значениям факторов и полученным в результате проведения опытов эксперимента значениям переменных отклика. Применение метода наименьших квадратов не зависит от распределений случайных переменных у₁, у₂, …, у_п отклика в опытах эксперимента. Для него необходимо только чтобы сделанные в разделе 7.1 допущения соблюдались. Методом наименьших квадратов ищутся такие значения параметров модели, при которых сумма квадратов разностей между наблюдаемыми в опытах значениями переменных у₁, у₂, …, у_п и соответствующими им ожидаемыми значениями Е(у₁), Е(у₂), …, Е(у_п) постулируемой модели (7.1.3) делается минимальной. При этом считается, что параметры q₀, q₁, q₂, …, q_р–1 являются переменными и ищутся такие их значения, при которых функция параметров в виде суммы квадратов

S(q₀, q₁, q₂, …, q_р–1)=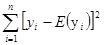

=,         (7.2.1)

принимает минимальное значение.

Чтобы найти результаты ,, ...,  оценки параметров, при которых функция S(q₀, q₁, q₂, …, q_р–1) принимает минимальное значение, нужно взять первые частные производные от этой функции по каждому параметру q₀, q₁, q₂, …, q_р–1, как сделано в предыдущей главе с двумя параметрами, и приравнять производные нулю. В итоге получается система из р уравнений, которая решается относительно q₀, q₁, q₂, …, q_р–1 и её решением являются результаты ,, ...,  оценки параметров. Эта процедура может быть представлена в более компактной матричной записи.

Теорема 7.2.1. Для постулируемой модели у=Xq+e, где X - матрица размеров пхр и ранга р<п, вектор =[,, ..., ] оценки параметров q₀, q₁, q₂, …, q_р–1, при котором функция S(q₀, q₁, q₂, …, q_р–1) принимает минимальное значение, находятся по формуле

Рекомендуемые материалы

=(X^ТX)^–1X^Тy.                                              (7.2.2)

Доказательство: В силу (П.2.12) и (П.2.19), выражение (7.2.1) можно записать так

S(q)=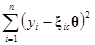

=(у–Xq)^Т(у–Xq),                                           (7.2.3)

где q^Т=[q₀, q₁, q₂, …, q_р–1] и x_iс=[1, x_i1,..., x_i(р–1)] является i-й строкой матрицы X модели. Если раскрыть скобки в выражении (у–Xq)^Т(у–Xq), то два из получаемых четырех членов могут быть объединены и в результате имеем

S(q)=y^Тy–2y^ТXq+q^ТX^ТXq.                                       (7.2.4)

По теоремам П.14.1 и П.14.2, беря производную от функции S(q) по q и приравнивая её нулевому вектору, получаем

=0–2X^Тy+2X^ТXq=0.

В итоге имеем нормальные уравнения метода наименьших квадратов в матричном виде

X^ТXq=X^Тy.                                                    (7.2.5)

По пункту 3 теоремы П.4 и пункту 1 теоремы П.6.4, а также следствию 1 теоремы П.6.3, если матрица X полного ранга, то матрица X^ТX невырожденная и решение нормальных уравнений имеет вид

=(X^ТX)^–1X^Тy.

Для найденного вектора  оценки параметров, если в функции S(q) вектор q=, то она принимает минимальное значение. Это можно доказать, взяв вторую производную функции S(q) по вектору q

=2X^ТX.

Матрица X невырожденная и по теореме П.6.3 матрица X^ТX положительно определённая, следовательно, при q= функция S(q) имеет минимальное значение [Schott (2016) стр.409-410].

□

Так как минимальное значение функции S(q) получается при q=, то вектор  называется вектором оценки методом наименьших квадратов. Заметим, что каждый элемент  вектора  является линейной функцией вектора у, то есть =a_jсy, где a_jс является j-й строкой матрицы (X^ТX)^–1X^Т. Использование линейной функции для оценки параметров не значит, что модель (7.1.3) линейна относительно x₁, x₂, ..., x_р–1. Эта модель линейна потому, что её функция линейна относительно параметров q₀, q₁, q₂, …, q_р–1.

Можно по-другому показать, что при q= действительно получается минимум функции S(q). Пусть вектор q будет результатом другой оценки, который может быть лучше чем , так что выражение (7.2.3) принимает вид

S(q)=(у–Xq)^Т(у–Xq).

В правой части этого уравнения в сомножителях, прибавляя и вычитая X, получаем

S(q)= (у–X+X–Xq)^Т(у–X+X–Xq)                           (7.2.6)

и после преобразования имеем

S(q)=(у–X)^Т(у–X)+(–q)^ТX^ТX(–q)+2(–q)^Т(X^Тy–X^ТX).  (7.2.7)

С учётом нормальных уравнений X^Тy=X^ТX третье слагаемое в правой части этого уравнения обращается в нуль. Второе слагаемое является положительно определенной квадратичной формой, при условии, что матрица X полного ранга (см. теорему П.6.4). Следовательно, S(q) принимает минимальное значение, когда =q.

Пример 7.2.1. Используем данные таблицы 7.1 для вычисления вектора  по формуле (7.2.2). Для расчётов воспользуемся программой Mathcad.

у=, X=, X^ТX=, X^Ту=,

(X^ТX)^–1= и =(X^ТX)^–1X^Тy=.

□

Условие раздельной оценки

Из (7.2.2) видно, что вектор  оценки параметров линейной модели является функцией вектора у значений случайных переменных отклика. Оценка каждого параметра модели должна быть отдельной от других оценок параметров. Преобразование вектора у в вектор  осуществляется умножением на матрицу (X^ТX)^–1X^Т. При этом заметим, что по пункту 1 теоремы П.2.3 матрица X^ТX размеров рхр состоит из произведений столбцов матрицы X, а вектор X^Тy состоит из произведений столбцов матрицы X на вектор у, то есть,

X^ТX= и X^Тy=.

Поэтому для раздельной оценки параметров возникает определённое требование к столбцам матрицы X модели.

Линейная комбинация вектор-столбцов 1, x₁, x₂,…, x_р–1 матрицы X образуется умножением их на соответствующие числа а₀, а₁,..., а_р–1 и сложением полученных произведений. Это позволяет определить линейную зависимость или независимость столбцов матрицы X. Комбинация столбцов 1, x₁, x₂,…, x_р–1 матрицы X называется линейно независимой, если равенство

а₀1+а₁x₁+…+а_р–1x_р–1=0                                            (7.2.8)

соблюдается при условии а₀=а₁=...=а_р–1=0. В противном случае, если существуют числа а₀, а₁,..., а_р–1 одновременно не равные нулю и такие, что выполняется равенство (7.2.8), то комбинация столбцов 1, x₁, x₂,…, x_р–1 называется линейно зависимой.

Теорема о ранге матрицы гласит, что ранг матрицы X равен максимальному числу линейно независимых столбцов или строк этой матрицы [Волосов (2006) стр.133]. В общем, матрица X размеров nxр, где n ≥р, имеет полный ранг р (по столбцам), если между столбцами не существует линейных зависимостей. Следовательно, для того чтобы р параметров модели оценивались раздельно необходимо использовать такой план эксперимента, который даёт матрицу X модели полного ранга р по столбцам.

Матрица X не должна содержать нулевых столбцов. Если в комбинацию её столбцов 1, x₁, x₂,…, x_р–1 входит столбец 0, все элементы которого равны нулю, то эта комбинация линейно зависима, а матрица X не имеет полного ранга по столбцам.

Если некоторые из столбцов 1, x₁, x₂,…, x_р–1 составляют сами по себе линейно зависимую комбинацию, то и вся комбинация столбцов x₀, x₁, x₂,…, x_р–1 линейно зависима. Это также приводит к тому, что матрица X не будет иметь полный ранг по столбцам и параметры не могут быть оценены раздельно.

Любые столбцы, входящие в линейно независимую комбинацию столбцов 1, x₁, x₂,…, x_р–1, сами по себе образуют линейно независимую комбинацию. Следовательно, если необходимо оценить меньше чем р параметров, то ненужные столбцы могут быть удалены из матрицы X полного ранга р по столбцам.

Если матрица X размеров nxр, где n ≥р, имеет полный ранг р по столбцам, то результат произведения её самой на себя X^TX является невырожденной матрицей. В противном случае, если существует q>0 линейно зависимых между собой столбцов матрицы X, то она имеет ранг р–q, а матица X^TX становится вырожденной и не имеет обратной матрицы. Поэтому, когда X имеет ранг р–q<р, то невозможно оценить р параметров вектора θ раздельно, а только р–q линейных их функций. Это показано на примере в разделе 6.2 предыдущей главы.

Свойства оценки параметров методом наименьших квадратов

В доказательстве теоремы 7.2.1 вектор  оценки был получен методом наименьших квадратов без учёта приведенных в разделе 7.1 допущений: Е(у)=Xq и С(у)=s²I. Модель у=Xq+e просто постулировалась и была сделана оценка её параметров. Если Е(у)≠Xq, то модель у=Xq+e все еще может использоваться, но при этом вектор  оценки может иметь неудовлетворительные свойства. А если С(у)≠s²I, то могут быть ещё дополнительные неблагоприятные последствия оценки. Однако, если допущения Е(у)=Xq и С(у)=s²I соблюдаются, то вектор  оценки имеет несколько отличных свойств.

Заметим также, что  - вектор случайных величин, меняющихся с изменением результатов опытов эксперимента. В этом разделе находится вектор его математического ожидания и матрица ковариаций (без допущения о распределении элементов вектора у), а в разделе 7.3 рассматривается вид его распределения, допуская, что переменные отклика распределены по нормальному закону. В следующих теоремах считается, что элементы матрицы X остаются постоянными при повторных опытах и эта матрица полного ранга.

Теорема 7.2.2. Если справедливо допущение Е(у)=Xq, то  является вектором несмещённой оценки вектора q.

Доказательство: Найдём математическое ожидание вектора

E()=E[(X^ТX)^–1X^Тy]

=(X^ТX)^–1X^ТE(у)            [в силу (3.6.4)]

=(X^ТX)^–1X^ТXq

=q.                                                                 (7.2.9)

□

Теорема 7.2.3. Если справедливо допущение С(у)=s²I, то матрица ковариаций вектора  имеет вид s²(X^ТX)^–1.

Доказательство: Найдём ковариационную матрицу вектора

С()=С[(X^ТX)^–1X^Тy]

=(X^ТX)^–1X^ТС(у)[(X^ТX)^–1X^Т]^Т     [в силу (3.6.10)]

=(X^ТX)^–1X^Т(s²I)X(X^ТX)^–1

=s²(X^ТX)^–1X^ТX(X^ТX)^–1

=s²(X^ТX)^–1.                                                    (7.2.10)

□

Пример 7.2.2. Используя обратную матрицу (X^ТX)^–1 для рассмотренной в разделе 6.2 простой линейной регрессии, получаем

С()=С==s²(X^ТX)^–1

=                              (7.2.11)

=.                                          (7.2.12)

Таким образом

D()=, D()= и C(,)=.

В разделе 6.2 найдены дисперсии D() и D(), но не получена ковариация C(,). При этом, если >0, то C(,) является отрицательной и результаты  и  оценки имеют отрицательную корреляцию. В этом случае, если  увеличивается от одной выборки к другой, то  стремится уменьшаться (при условии, что значения переменной x остаются теми же).

□

Пример 7.2.3. Для данных из таблицы 7.1 матрица (X^ТX)^–1 получена в примере 7.2.1. Таким образом, матрица ковариаций С() имеет вид

С()=s²(X^ТX)^–1=s².

Отрицательное значение С(,) = –1,004х10^–3 показывает, что в повторных выборках значений переменных отклика (используя те же 14 значений переменных x₁ и x₂) величины  и  будет стремиться изменяться в противоположных направлениях, то есть, увеличение одной будет сопровождаться уменьшением другой.

□

В дополнение к Е()=q и С()=s²(X^ТX)^–1 третьим важным свойством вектора  является то, что, при справедливости допущений раздела 7.1, дисперсия результата  оценки каждого параметра модели минимальна.

Теорема 7.2.4 (Гаусса-Маркова). Если соблюдаются допущения Е(у)=Xq и С(у)=s²I, то среди всех возможных линейных несмещенных результатов оценки параметров модели найденные методом наименьших квадратов  (j=0, 1, ..., р–1) имеют наименьшие дисперсии.

Доказательство: Рассмотрим вектор Ау линейной оценки вектора q и будем искать такую матрицу А, для которой вектор Ау является вектором несмещённой оценки вектора q с минимальной дисперсией. Для того чтобы вектор Ау был вектором несмещённой оценки вектора q необходимо чтобы Е(Ay)=q. Исходя из допущения Е(у)=Xq, это может быть выражено так

Е(Ay)=АЕ(у)=AXq=q,

что дает условие несмещённости в виде

AX=I,

так как равенство AXq=q должно выполняться для любых возможных значений вектора q [см. (П.4.4)].

Матрица ковариаций вектора Ay оценки получается в виде

С(Ay)=A(s²I)A^Т=s²AA^Т.

Дисперсии величин  располагаются по диагонали матрицы s²AA^Т, поэтому матрица A должна быть выбрана так (при условии AX=I), чтобы диагональные элементы матрицы AA^Т получились минимальными. Для совместного рассмотрения вектора Ay с вектором =(X^ТX)^–1X^Тy прибавим и вычтем (X^ТX)^–1X^Т из А чтобы получить следующее равенство

AA^Т=[А–(X^ТX)^–1X^Т+(X^ТX)^–1X^Т][А–(X^ТX)^–1X^Т+(X^ТX)^–1X^Т]^Т.

Преобразуя его относительно членов А–(X^ТX)^–1X^Т и (X^ТX)^–1X^Т, получаем четыре члена, два из которых уничтожаются, при условии AX=I. В результате имеем

AA^Т=[А–(X^ТX)^–1X^Т][А–(X^ТX)^–1X^Т]^Т+(X^ТX)^–1.                    (7.2.13)

В правой части матрица [А–(X^ТX)^–1X^Т][А–(X^ТX)^–1X^Т]^Т неотрицательно определённая (см. теорему П.6.4) и по пункту 2 теоремы П.6.1 её диагональные элементы больше или равны нулю. Эти диагональные элементы становятся равными нулю при А=(X^ТX)^–1X^Т. Такая матрица А также удовлетворяет условию несмещенности AX=I. Получающийся в итоге результат оценки вектора q с минимальной дисперсией имеет вид

Ау=(X^ТX)^–1X^Тy,

что равносильно вектору  оценки методом наименьших квадратов.

□

Теорема Гаусса-Маркова иногда формулируется следующим образом. Если соблюдаются допущения Е(у)=Xq и С(у)=s²I, то результаты ,, ...,  оценки параметров модели методом наименьших квадратов являются наилучшими линейными несмещёнными оценками. В этом выражении слово наилучшие означает минимальные дисперсии результатов оценки, а слово линейные указывает, что они являются линейными функциями вектора у.

Замечательной особенностью теоремы Гаусса-Маркова является её применимость к любым распределениям случайных переменных отклика. По этой теореме оценка параметров с наименьшей дисперсией получается при любых распределениях случайных переменных вектора у и не требуется, чтобы они были распределены по нормальному закону. Однако, в доказательстве теоремы использованы допущения Е(у)=Xb и С(у)=s²I. А если они не соблюдаются, то вектор  может быть смещённым или каждый его элемент из ,, ...,  может иметь дисперсию больше, чем при некотором другом методе оценки.

Теорема Гаусса-Маркова применима также к некоторой линейной комбинации результатов ,, ...,  оценки следующим образом.

Следствие 1. Если соблюдаются допущения Е(у)=Xq и С(у)=s²I, то для линейной комбинации a^Тq величина a^Т является наилучшим линейным несмещённым результатом оценки, где =(X^ТX)^–1X^Тy - вектор оценки методом наименьших квадратов.

Доказательство: Чтобы линейная оценка величины с^Ту была несмещённой для всех возможных векторов q необходимо чтобы Е(с^Ту)=с^ТXq=a^Тq, что требует с^ТX=a^Т. Для выражения дисперсии D(с^Ту) через D(a^Т)=D[a^Т(X^ТX)^–1X^Тy] запишем её в виде

D(с^Ту)=s²с^Тс=s²[c–X(X^ТX)^–1a+X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a+X(X^ТX)^–1a].

Далее, если с^ТX=a^Т, то выражение [c–X(X^ТX)^–1a+X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a+X(X^ТX)^–1a], преобразованное относительно членов [c–X(X^ТX)^–1a] и X(X^ТX)^–1a, принимает вид

[c–X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a]+[X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a]+[c–X(X^ТX)^–1a]^Т[X(X^ТX)^–1a]

+[X(X^ТX)^–1a]^Т[X(X^ТX)^–1a]

   = [c–X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a]+a^Т(X^ТX)^–1X^Тc–a^Т(X^ТX)^–1a+c^Т X(X^ТX)^–1a–a^Т(X^ТX)^–1a

+a^Т(X^ТX)^–1a

   = [c–X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a]+a^Т(X^ТX)^–1a–a^Т(X^ТX)^–1a+a^Т(X^ТX)^–1a

   = [c–X(X^ТX)^–1a]^Т[c–X(X^ТX)^–1a]+a^Т(X^ТX)^–1a

Оно имеет минимум при c=X(X^ТX)^–1a. Следовательно, с^Ту=a^Т(X^ТX)^–1X^Ту =a^Т и Е(с^Ту)=Е(a^Т)=a^Тq.

□

Заметим, что в теореме 7.2.4 (Гаусса-Маркова) рассматривается вектор  оценки при заданной матрице X. После того как матрица X задана, дисперсии результатов ,,...,  оценки делаются наименьшими, если они вычисляются по формуле =(X^ТX)^–1X^Тy. Тем не менее, по теореме 7.2.3 вектор  имеет ковариационную матрицуs²(X^ТX)^–1 и, следовательно, дисперсии D() и ковариации С(,) (k=0, 1, ..., р–1) результатов оценки параметров зависят от свойств столбцов матрицы X. Линейная независимость столбцов обеспечивает раздельную оценку параметров модели. Далее рассмотрим, что получается, если столбцы матрицы X ортогональны между собой.

Условие раздельной и некоррелированной оценки

Помимо требования раздельной оценки параметров модели возникает также требование их некоррелированной оценки. Параметры выражают степень влияния на переменные отклика соответствующих им факторов, и некоррелированная их оценка позволяет найти такие величины их оценки, которые статистически взаимно независимы. Для достижения раздельной оценки линейно независимые вектор-столбцы матрицы модели формируют векторное пространство Ст(X), а для некоррелированной оценки параметров в этом векторном пространстве должно выполняться скалярное произведение векторов и все вектор-столбцы должны быть взаимно ортогональны.

Положим, что в функции Е(у)=Xq модели матрица X имеет полный ранг и разделена на столбцы в виде

X=[1, x₁, x₂,…, x_р–1],

где все вектор-столбцы 1, x₁, x₂,…, x_р–1 ортогональны между собой. В этом случае можно получить формулу =(X^TX)^–1X^Ty оценки параметров в разделённом виде

==.

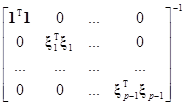
Следовательно, оценку каждого параметра модели можно сделать отдельно по формуле

=.                                          (7.2.14)

Так получается в результате оценки методом наименьших квадратов одного параметра модели у=x_jq_j+e. Это значит, что результат оценки параметра q_j не меняется, если любые другие составляющие вектора q параметров отсутствуют или равны нулю.

Ортогональные между собой вектор-столбцы матрицы X линейно независимы [Seber (2008) стр.16]. Следовательно, матрица X с взаимно ортогональными столбцами удовлетворяет также и требованию раздельной оценки параметров. Эта матрица позволяет осуществлять раздельную и некоррелированную, то есть, статистически независимую оценку параметров. Таким образом, если параметры линейной модели оцениваются методом наименьших квадратов и столбцы матрицы модели взаимно ортогональны, то оценка параметров получается раздельной, некоррелированной, несмещённой и с наименьшей дисперсией. Такая оценка наиболее желательна, так как в результате получается модель удобная для анализа и простого изменения числа её членов при добавлении или исключении анализируемых факторов.

Оценка ожидаемых значений переменных отклика

Имея вектор =(X^ТX)^–1X^Тy оценки параметров, можно найти вектор оценки переменных отклика. Если функция модели определяется в виде математического ожидания переменной отклика E(у_i)=q ₀+q₁x_i1+q₂x_i2+...+q_р–1x_i(р–1), то оценка ожидаемого значения переменной отклика делается по формуле

=+x_i1+x_i2+…+x_i(р–1).

Результат оценки обычно обозначается , но является результатом оценки не самой переменной отклика у_i, а ожидаемого её значения E(у_i), соответствующего набору значений факторов в конкретном i-м опыте эксперимента. Для всех опытов эксперимента, выполняемых при наборах значений переменных x₁, x₂,..., x_р–1, заданных в виде матрицы плана эксперимента, и полученной на её основе матрицы X модели, имеем

==X.                                                           (7.2.15)

Вектор  оценки ожидаемых значений переменных отклика соответствует вектору у наблюдаемых значений переменных отклика в n опытах эксперимента. Он называется вектором оцениваемых значений переменных отклика.

Ковариационная матрица вектора  легко получается по формуле (7.2.10) для С(). Таким образом, имеем

С[]=X(X^TX)^–1X^Ts².                                                (7.2.16)

Вектор  оценки ожидаемых значений переменных отклика может быть представлен также в виде

=Рy,                                                            (7.2.17)

где матрица Р=X(X^TX)^–1X^T симметричная и идемпотентная. Она является матрицей ортогонального проецирования вектора у в пространство столбцов Ст(X) матрицы X.

Вектор e случайных ошибок модели (7.1.3) можно представить выражением

у–Е(у)=(у–)+[–Е(у)].

Произведение слагаемых в его правой части

(у–)^Т[–Е(у)]=(у–Ру)^Т[Рy–Е(у)]

=у^Т(I_n–Р)[Рy–Xq)]

=0,

так как РX=X и Р²=Р. Следовательно длина разности y–Е(у) векторов в квадрате

||y–Е(у)||²=||у–||²+||–Е(у)||²

≥||у–||²

Обратите внимание на лекцию "7.2 Кочевники Восточной Европы в средние века".

будет минимальной, если и только если Е(у)= и разность векторов у– образует вектор перпендикулярный пространству оценки Ст(X) формируемому столбцами матрицы X, как показано на Рис.7.2.1. А так как вектор разности у–перпендикулярен вектор-столбцам матрицы X, то X^Т(у–)=0 или

X^Ту=X^Т.                                                      (7.2.18)

Здесь вектор , будучи однозначной ортогональной проекцией вектора у в пространство вектор-столбцов матрицы X, однозначно определён.

Если считать, что столбцы матрицы X линейно независимы, то существует однозначно определённый вектор , при котором =X [Seber, Lee (2003) стр.37]. Тогда, подставляя X вместо  в (7.2.18), имеем выражение X^Ту=X^ТX нормальных уравнений метода наименьших квадратов. Так как матрица X имеет ранг р, то матрица X^ТX положительно определённая и поэтому невырожденная. Следовательно, нормальные уравнения имеют единственное решение данное выражением (7.2.2). Вектор  называется вектором оценки обычным методом наименьших квадратов вектора q параметров модели.

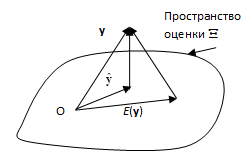
Рис.7.2.1. Геометрическое представление вектора у в n-мерном евклидовом пространстве и векторов Е(у) и  в пространстве Ст(X) оценки столбцов матрицы X