Оценка параметров модели и дисперсии
6.2. Оценка параметров модели и дисперсии
Результаты оценки параметров
Для оценки параметров q0, q1 и дисперсии s2 используется случайная выборка у1, у2, ..., уп наблюдений переменных отклика в п опытах эксперимента и соответствующие им числовые значения x1, x2, ..., xп влияющей на отклик переменной x. Для получения результатов  и
и  оценки параметров используется метод наименьших квадратов, который не требует никаких допущений о распределении случайных переменных модели.
оценки параметров используется метод наименьших квадратов, который не требует никаких допущений о распределении случайных переменных модели.
Методом наименьших квадратов ищутся такие результаты  и
и  оценки параметров q0 и q1, которые делают минимальной сумму квадратов разностей
оценки параметров q0 и q1, которые делают минимальной сумму квадратов разностей
 =
= (6.2.1)
(6.2.1)
наблюдаемых в п опытах значений уi переменных отклика и их ожидаемых значений Е(уi)=q0+q1xi в соответствии с постулируемой моделью (6.1.1). Эта сумма квадратов является функцией параметров q0 и q1 и поэтому обозначается S(q0, q1). Для нахождения  и
и  , при которых функция S(q0, q1)=
, при которых функция S(q0, q1)= принимает минимальное значение, берутся её первые частные производные по q0 и q1 и приравниваются нулю:
принимает минимальное значение, берутся её первые частные производные по q0 и q1 и приравниваются нулю:
 =–2
=–2 =0, (6.2.2)
=0, (6.2.2)
 =–2
=–2 =0. (6.2.3)
=0. (6.2.3)
Эти уравнения можно записать соответственно в виде
Рекомендуемые материалы
 =0 и
=0 и  =0.
=0.
Решение первого уравнения относительно q0 даёт
q0=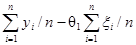
= –q1
–q1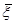 , (6.2.4)
, (6.2.4)
где  =
= и
и 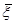 =
=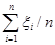 . Подставляя его во второе уравнение, получаем
. Подставляя его во второе уравнение, получаем
 =0
=0
и отсюда находим формулу для вычисления 
 =
= =
=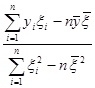
=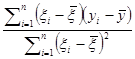 . [в силу (1.4.3)] (6.2.5)
. [в силу (1.4.3)] (6.2.5)
Подставляя в (6.2.4) вместо  его найденное значение
его найденное значение  , получаем формулу расчёта
, получаем формулу расчёта 
 =
= –
–
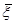 . (6.2.6)
. (6.2.6)
Чтобы убедиться, что при результатах  и
и  оценки параметров функция S(q0, q1) принимает минимальное значение, нужно рассмотреть вторые производные этой функции по q0 и q1. Вторые производные функции S(q0, q1) получаются соответственно
оценки параметров функция S(q0, q1) принимает минимальное значение, нужно рассмотреть вторые производные этой функции по q0 и q1. Вторые производные функции S(q0, q1) получаются соответственно  =2п и
=2п и  =2
=2 . Значения этих производных положительные, поэтому при q0=
. Значения этих производных положительные, поэтому при q0= и q1=
и q1= функция S(q0, q1) принимает минимальное значение [Выгодский (2006) стр. 429; Khuri (2003) стр. 114].
функция S(q0, q1) принимает минимальное значение [Выгодский (2006) стр. 429; Khuri (2003) стр. 114].
Заметим, что при выполнении оценки по формулам (6.2.5) и (6.2.6) не используются допущения раздела 6.1. Получаемые из уравнения  =
= +
+ xi результаты оценки ожидаемых значений переменных отклика оценивают их значения, полученные в результате эксперимента, и которые на самом деле возможно должны моделироваться нелинейной функцией. Тем не менее, если три допущения раздела 6.1 соблюдаются, то полученные методом наименьших квадратов
xi результаты оценки ожидаемых значений переменных отклика оценивают их значения, полученные в результате эксперимента, и которые на самом деле возможно должны моделироваться нелинейной функцией. Тем не менее, если три допущения раздела 6.1 соблюдаются, то полученные методом наименьших квадратов  и
и  являются несмещёнными результатами оценки и имеют наименьшую дисперсию среди всех возможных линейных несмещенных результатов оценки.
являются несмещёнными результатами оценки и имеют наименьшую дисперсию среди всех возможных линейных несмещенных результатов оценки.
Уравнения (6.1.1) моделей для п опытов эксперимента можно представить в матричном или векторном видах
у=Xq+e
=q01+q1x+e, (6.2.7)
где у= - вектор полученных в опытах значений переменных отклика, X=
- вектор полученных в опытах значений переменных отклика, X= - матрица модели, q=
- матрица модели, q= - вектор параметров модели и e=
- вектор параметров модели и e= - вектор ошибок. В этом случае оценка параметров модели может быть сделана тоже с использованием матриц. Так, произведение матрицы модели на себя принимает вид XТX=
- вектор ошибок. В этом случае оценка параметров модели может быть сделана тоже с использованием матриц. Так, произведение матрицы модели на себя принимает вид XТX= , а обратная этого произведения (XТX)–1=
, а обратная этого произведения (XТX)–1= . Произведение матрицы модели на вектор значений переменных отклика имеет вид XТy=
. Произведение матрицы модели на вектор значений переменных отклика имеет вид XТy= . В теореме 7.2.1 следующей главы доказано, что оценки
. В теореме 7.2.1 следующей главы доказано, что оценки  и
и  получаются в результате решения нормальных уравнений XТXq=XТy по формуле
получаются в результате решения нормальных уравнений XТXq=XТy по формуле  =(XТX)–1XТy, то есть
=(XТX)–1XТy, то есть
 =
= =
= . (6.2.8)
. (6.2.8)
Результаты  и
и  оценки здесь такие же, как по формулам (6.2.5) и (6.2.6). Это можно показать так
оценки здесь такие же, как по формулам (6.2.5) и (6.2.6). Это можно показать так
 =
= =
= =
=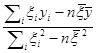 ,
,
что, как и в (6.2.5). Для  начнём с выражения (6.2.6)
начнём с выражения (6.2.6)
 =
= –
–
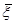 =
= –
–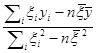
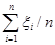
= –
–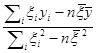
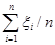
= .
.
Второй и четвёртый члены числителя сокращаются и, как в (6.2.7), получаем
 =
= .
.
Пример 6.2.1. В интегральной микросхеме коэффициент (у) усиления транзистора между эмиттером и коллектором зависит от двух контролируемых в процессе напыления переменных: эмиттерной дозы (x в единицах по 1014 ионов) и времени (x1 в мин.) разгонки примеси эмиттера. Здесь рассмотрим часть данных для 10 образцов после напыления при x1=225, сведённых в таблицу 6.2.1 [Myers и соавт. (2016) стр.17-18].
Таблица 6.2.1. Значения коэффициента (у) усиления транзистора и переменной x
| Опыты | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 4,00 | 4,60 | 4,20 | 4,10 | 4,60 | 4,30 | 4,00 | 4,70 | 4,30 | 4,72 |
| у | 1636 | 1506 | 1272 | 1270 | 1269 | 1555 | 1260 | 1146 | 1276 | 1225 |
По формулам (6.2.5) и (6.2.6) находятся  =2201,7 и
=2201,7 и  =–197,6. Таким образом, уравнение оценки ожидаемых значений коэффициента усиления в зависимости от переменной x получается в виде
=–197,6. Таким образом, уравнение оценки ожидаемых значений коэффициента усиления в зависимости от переменной x получается в виде
 =2201,7–197,6x.
=2201,7–197,6x.
На Рис. 6.1 показаны график зависимости  от x в виде прямой линии синим цветом вместе с 10 точками с координатами (x, у). Из рисунка, очевидно, что наклон
от x в виде прямой линии синим цветом вместе с 10 точками с координатами (x, у). Из рисунка, очевидно, что наклон  является скоростью изменения
является скоростью изменения  при изменении x, а значение
при изменении x, а значение  равно значению
равно значению  при x=0.
при x=0.
Кажущаяся линейной зависимость на Рис. 6.1 не устанавливает причинно следственной зависимости коэффициента усиления от эмиттерной дозы (выводы, которые здесь можно сделать, см. в разделе 6.3). Допущение D(ei)=s2 (постоянной дисперсии) для всех i=1, 2, ..., 10 представляется разумным.
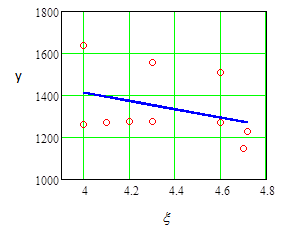
Рис. 6.1. Линия регрессии и данные эксперимента для коэффициента усиления и эмиттерной дозы.
□
Объяснение результатов и условие их раздельной оценки
Обсудим теперь смысл результатов оценки параметров, использованных в уравнении  =2201,7–197,6x оценки ожидаемых значений переменных отклика из примера 6.2.1. Заметим, что на Рис.6.1 результат 2201,7 оценки параметра q0 равный
=2201,7–197,6x оценки ожидаемых значений переменных отклика из примера 6.2.1. Заметим, что на Рис.6.1 результат 2201,7 оценки параметра q0 равный  при x=0, не показана. За пределами интервала от 4,00 до 4,72 единиц переменной x, при которых коэффициент усиления транзистора действительно измерялся, прямая линия на Рис.6.1 не показана, так как нет данных, чтобы проверить её обоснованность за пределами этого интервала. В частности, результат 2201,7 должен расцениваться просто как точка, через которую проходит прямая линия в диапазоне значений переменной x опытов эксперимента.
при x=0, не показана. За пределами интервала от 4,00 до 4,72 единиц переменной x, при которых коэффициент усиления транзистора действительно измерялся, прямая линия на Рис.6.1 не показана, так как нет данных, чтобы проверить её обоснованность за пределами этого интервала. В частности, результат 2201,7 должен расцениваться просто как точка, через которую проходит прямая линия в диапазоне значений переменной x опытов эксперимента.
Второй результат –197,6 оценки параметра q1 в уравнении оценки ожидаемых значений переменных отклика определяет наклон линии в используемых единицах измерений. Таким образом, по уравнению  =2201,7–197,6x величина
=2201,7–197,6x величина  уменьшается на 197,6 единиц при изменении на единицу переменной x.
уменьшается на 197,6 единиц при изменении на единицу переменной x.
В статистическом моделировании под планом эксперимента понимается перечень используемых в опытах эксперимента значений влияющей на отклик переменной. Так, в примере 6.2.1 с коэффициентом усиления транзистора перечень представленных в таблице 6.2.1 значений переменной ξ является планом эксперимента. Здесь план представляется вектором значений эмиттерной дозы, но в общем случае для нескольких влияющих на отклик переменных план представляет собой матрицу значений этих переменных, строки которой являются наборами их значений, устанавливаемых в опытах эксперимента. Столбцы этой матрицы используются для оценки параметров модели и для раздельной их оценки столбцы должны удовлетворять определённому условию.
Рассмотрим это условие на примере [Box, Draper (2007) стр. 35]. В нём имеется уравнение линейной модели y=θ1x1+θ2x2+e, где переменной (y) отклика является скорость протекания химической реакции, а x1 и x2 - процентные содержания двух катализаторов А и В, влияющих на скорость реакции. Полагается, что выбран такой план эксперимента, в котором значения x1 и x2 оказались пропорциональны один другому, так что для каждого опыта x2=δx1. Тогда, например, при δ=2 в каждом опыте процентное содержание катализатора В будет в два раза больше, чем катализатора А. В этом случае матрица модели имеет, например, вид X= . Тогда уравнение y=θ1x1+θ2x2+e модели может быть записано в виде
. Тогда уравнение y=θ1x1+θ2x2+e модели может быть записано в виде
y=θ1x1+θ2δx1+e
=(θ1+δθ2)x1+e
=δ–1(θ1+δθ2)x2+e.
Методом наименьших квадратов могут быть найдены нормальные уравнения для оценки параметров θ1 и θ2, но они не обеспечивают единственности их оценки. Эти параметры не могут быть оценены раздельно. В этом случае можно оценить только их линейную комбинацию θ1+δθ2. Причина этого в том, что когда x2=δx1, то влияние на переменную отклика переменной x1 (катализатор А) полностью неразличимо от влияния переменной x2 (катализатор В). Равенство x2=δx1 означает, что x2–δx1=0. В общем, это происходит всегда, когда линейная зависимость вида α1x1+α2x2=0 (для данного примера α1=–δ, α2=1) связывает линейно зависимые столбцы матрицы X.
В начале раздела П.4 приложения даётся определение линейно независимых векторов и столбцов матрицы. Следовательно, для раздельной оценки параметров модели вектор-столбцы матрицы модели должны быть линейно независимы. Это условие соблюдается для столбцов матрицы модели в примере 6.2.1.
Математические ожидания и дисперсии результатов оценки
Результаты  и
и  оценки параметров модели являются линейными функциями значений у1, у2, ..., уп переменных отклика. Используя три допущения раздела 6.1, можно получить следующие математические ожидания и дисперсии для
оценки параметров модели являются линейными функциями значений у1, у2, ..., уп переменных отклика. Используя три допущения раздела 6.1, можно получить следующие математические ожидания и дисперсии для  и
и  .
.
В числителе правой части выражения (6.2.5) имеем
 =
=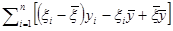
=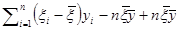
= .
.
Тогда формула (6.2.5) принимает вид
 =
= .
.
Теперь, используя первое допущение Е(уi)=q0+q1xi раздела 6.1, получаем
Е( )=
)= =
=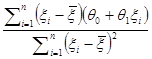
= =
=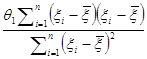
=q1. (6.2.9)
Математическое ожидание для  находится следующим образом
находится следующим образом
E( )=E(
)=E( –
–
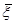 )=E(
)=E( )–E(
)–E( )
)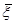
= –q1
–q1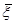 =
= –q1
–q1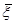
=q0+q1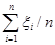 –q1
–q1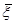 =q0. (6.2.10)
=q0. (6.2.10)
Таким образом, математические ожидания для  и
и  равны самим оцениваемым параметрам и поэтому их результаты оценки являются несмещёнными. В векторном виде для модели (6.2.7) это можно записать так
равны самим оцениваемым параметрам и поэтому их результаты оценки являются несмещёнными. В векторном виде для модели (6.2.7) это можно записать так
E( )=q. (6.2.11)
)=q. (6.2.11)
Дисперсия  определяется с использованием его выражения по формуле (6.2.5), а также второго D(уi)=s2 и третьего C(уi, уj)=0 допущений раздела 6.1. В силу (3.2.8), имеем
определяется с использованием его выражения по формуле (6.2.5), а также второго D(уi)=s2 и третьего C(уi, уj)=0 допущений раздела 6.1. В силу (3.2.8), имеем
D( )=
)= =
=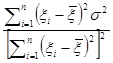
=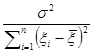 . (6.2.12)
. (6.2.12)
По формуле (6.2.6) для  можно записать
можно записать
 =
= –
–
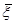 =
= –
–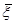
 .
.
Тогда дисперсия  находится следующим образом
находится следующим образом
D( )=D
)=D =
=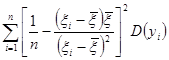
= s2
s2
=s2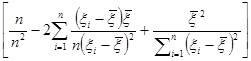
=s2 . (6.2.13)
. (6.2.13)
Обратим внимание, что при нахождении математического ожидания Е( ) и дисперсии D(
) и дисперсии D( ) рассматриваются случайные изменения
) рассматриваются случайные изменения  от выборки к выборке значений случайных переменных уi. Полагается, что n значений x1, x2, ..., xп влияющей на отклик переменной x остаются теми же в опытах эксперимента при получении выборочных значений случайных переменных уi, так что дисперсии D(
от выборки к выборке значений случайных переменных уi. Полагается, что n значений x1, x2, ..., xп влияющей на отклик переменной x остаются теми же в опытах эксперимента при получении выборочных значений случайных переменных уi, так что дисперсии D( ) и D(
) и D( ) постоянны.
) постоянны.
Матрица дисперсий и ковариаций вектора  оценки параметров модели находится в виде
оценки параметров модели находится в виде
D( )=E{[
)=E{[ –E(
–E( )][
)][ –E(
–E( )]T}=(XТX)–1XТE{[y–E(y)][yT–E(yT)]}X(XТX)–l
)]T}=(XТX)–1XТE{[y–E(y)][yT–E(yT)]}X(XТX)–l
= (XТX)–lXTE(eeT)X(XТX)–l
= (XТX)–ls2. (6.2.14)
Условия оценки параметров с минимальной дисперсией
Из выражения (6.2.12) видно, что дисперсия D( ) становится минимальной, когда сумма
) становится минимальной, когда сумма 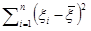 максимальна. Если значения xi влияющей на отклик переменной находятся в интервале а≤xi≤b, где а и b - крайние числа интервала, то при четном п сумма
максимальна. Если значения xi влияющей на отклик переменной находятся в интервале а≤xi≤b, где а и b - крайние числа интервала, то при четном п сумма 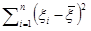 становится максимальной, если в опытах эксперимента одна половина значений переменной x выбирается равной а, а другая половина равной b. Это можно показать следующим образом.
становится максимальной, если в опытах эксперимента одна половина значений переменной x выбирается равной а, а другая половина равной b. Это можно показать следующим образом.
Пусть р значений переменной x равны а, а оставшиеся п–р значений равны b. Тогда усреднённое значение этой переменной 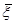 =[рa+(n–р)b]/n. В этом случае
=[рa+(n–р)b]/n. В этом случае 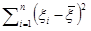 можно представить в виде
можно представить в виде
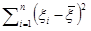 =р{a–[рa+(n–р)b]/n}2+(n–р){b–[рa+(n–р)b]/n}2
=р{a–[рa+(n–р)b]/n}2+(n–р){b–[рa+(n–р)b]/n}2
=р{[na–рa–nb+рb]/n}2+(n–р){[nb–рa–nb+рb]/n}2
=р{[n(a–b)–р(a–b)]/n}2+(n–р)[–р(a–b)/n]2
=р(n–р)2(a–b)2/n2+(n–р)р2(a–b)2/n2
=[р(n–р)2+р2(n–р)](a–b)2/n2
=р(n–р)(n–р+р)(a–b)2/n2
=р(n–р)(a–b)2/n.
Далее возмём первую производную от полученного выражения по р и приравняем её нулю
 =(n–2р)(a–b)2/n=0.
=(n–2р)(a–b)2/n=0.
Отсюда получаем р=п/2. А если взять вторую производную, то получаем
 =–2(a–b)2/n.
=–2(a–b)2/n.
Вторая производная получается отрицательной, следовательно при р=п/2 достигается максимум суммы 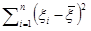 .
.
Это преимущество, что при проведении опытов эксперимента с использованием только двух значений, называемых также уровнями фактора x, достигается минимальная дисперсия оценки коэффициента регрессии, используется в планировании двухуровневых факторных экспериментов. При планировании таких экспериментов для каждого фактора выбираются только два значения или уровня.
Кроме этого, в силу (6.2.13), очевидно, что дисперсия D( ) становится минимальной, когда
) становится минимальной, когда 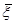 =0. Для этого при обработке результатов двухуровневых факторных экспериментов каждый влияющий на отклик фактор нормируется по формуле (2.6.4) чтобы усреднённое нормированного фактора было равно нулю.
=0. Для этого при обработке результатов двухуровневых факторных экспериментов каждый влияющий на отклик фактор нормируется по формуле (2.6.4) чтобы усреднённое нормированного фактора было равно нулю.
Ортогонализация столбцов матрицы модели
При соблюдении первого допущения раздела 6.1, математическое ожидание вектора случайных переменных отклика модели (6.2.7) имеет вид Е(у)=Xq. Если в это выражение вместо вектора q подставить вектор  =(XТX)–1XТy его оценки, то получается вектор оценки ожидаемых значений случайных переменных
=(XТX)–1XТy его оценки, то получается вектор оценки ожидаемых значений случайных переменных  ≡
≡ =X
=X . Разность векторов у и
. Разность векторов у и  даёт вектор остатков или остаточных ошибок
даёт вектор остатков или остаточных ошибок
е=у– =у–X(XТX)–1XТy
=у–X(XТX)–1XТy
=[I–X(XТX)–1XТ]y (6.2.15)
Произведение этого вектора и матрицы X даёт нулевой вектор
XТе=XТ[I–X(XТX)–1XТ]y=[XТ–XТ]y=0.
По определению произведения матрицы на вектор это значит, что произведение вектора е с любым вектор-столбцом матрицы X даёт нулевой результат.
Если при планировании эксперимента векторы столбцы матрицы X не сделаны ортогональными, то на практике они обычно получаются не ортогональными. Это видно из примера 6.2.1, где первый и второй столбцы не ортогональны, то есть 1Тx≠0. Однако можно найти составляющий вектор xо вектора x, который ортогонален вектору 1, и переписать функцию модели с использованием ортогональных векторов. Для нахождения вектора xо, являющегося составляющим вектора x и ортогонального вектору 1, воспользуемся тем, что вектор е остатков ортогонален векторам 1 и x. Временно считая x вектором переменных отклика и 1 вектором значений влияющей на отклик переменной, методом наименьших квадратов получим оценку вектора ожидаемых значений отклика x в виде  =4,352x1. В силу (6.2.15), вектор остатков для данных примера 6.2.1находится так xо= x–
=4,352x1. В силу (6.2.15), вектор остатков для данных примера 6.2.1находится так xо= x– = x–4.352x1, что в численном выражении имеет вид
= x–4.352x1, что в численном выражении имеет вид
xоТ=[–0,352 0,248 –0,152 –0,252 0,248 –0,052 –0,352 0,348 –0,052 0,368].
Теперь перепишем функцию модели (6.2.7) в виде
Е(у)=θ01+θ1x+4,352θ11–4,352θ11
=(θ0+4,352θ1)1+θ1(x–4,352x1),
откуда получаем
Е(у)=θ1+θ1xо,
где θ=θ0+4,352θ1. Для такой функции модели имеем матрицу Xо=[1, xо] с использованием которой вычисляем
(XоТXо)–1= , XоТy=
, XоТy= и
и  =
= =
= .
.
И последним найдём также функцию Е(у)=θ01 модели, где параметр θ0 тоже оценивается методом наименьших квадратов по формуле  =(1Т1)–11Тy=1341,5.
=(1Т1)–11Тy=1341,5.
Теперь можно сравнить три выражения, полученные для оценки вектора ожидаемых значений переменных отклика:
Ø Для модели с одним параметром  =1341,5x1
=1341,5x1
Ø Для модели с двумя параметрами  =2201,7x1–197,6x
=2201,7x1–197,6x
Ø Для модели с ортогональными столбцами её матрицы  =1341,5x1–197,6xо
=1341,5x1–197,6xо
Из сравнения делаем следующие заключения:
1. Так как векторы 1 и xо ортогональны, то коэффициент перед вектором 1 в модели с ортогональными столбцами её матрицы и двумя параметрами является тем же, что и коэффициент перед 1 в модели с одним параметром.
2. Коэффициент перед вектором xо в модели с ортогональными столбцами её матрицы является тем же, что и коэффициент перед вектором x в модели с двумя параметрами и не ортогональными столбцами её матрицы.
Полученные выше выражения оценки представлены графически на Рис.6.2.1.
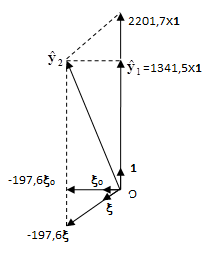
Рис. 6.2.1. Плоскость оценки векторов ожидаемых значений переменных отклика тремя моделями.
Вектор 1 и ортогональный ему вектор xо, как и векторы 1 и x, могут использоваться для задания плоскости, где расположен вектор  оценки ожидаемых значений переменных отклика. При не ортогональности базисных векторов 1 и x конец вектора
оценки ожидаемых значений переменных отклика. При не ортогональности базисных векторов 1 и x конец вектора  имеет координаты 2201,7x1 и –197,6x. При ортогональности базисных векторов 1 и xо, тот же конец вектора
имеет координаты 2201,7x1 и –197,6x. При ортогональности базисных векторов 1 и xо, тот же конец вектора  имеет координаты 1341,5x1 и –197,6xо.
имеет координаты 1341,5x1 и –197,6xо.
Таким образом, проведённый анализ показывает, что если матрица модели с двумя параметрами имеет ортогональные вектор-столбцы, то параметры модели оцениваются независимо друг от друга и от выбираемой линейной функции модели. При этом заметим, что столбцы матрицы модели с двумя параметрами можно сделать также ортогональными, если подвергнуть нормированию переменную x, как показано в разделе 6.5 этой главы.
Оценка дисперсии
Методом наименьших квадратов невозможно оценить дисперсию D(уi)=s2. Нахождение минимума функции S(q0, q1) дает только результаты  и
и  оценки параметров модели. Для оценки дисперсии используется выражение (3.2.2), то есть,
оценки параметров модели. Для оценки дисперсии используется выражение (3.2.2), то есть,
D(уi)=E[уi–E(уi)]2.
В опытах эксперимента по второму допущению раздела 6.1 дисперсия s2 считается одинаковой для всех переменных уi (i =1, 2, ..., п) отклика. Используя обозначение  для результата оценки ожидаемого значения E(уi) случайной переменной отклика, дисперсия s2 оценивается выражением
для результата оценки ожидаемого значения E(уi) случайной переменной отклика, дисперсия s2 оценивается выражением
s2= =
= =
= , (6.2.16)
, (6.2.16)
где  и
и  даются формулами (6.2.5) и (6.2.6), а SE=
даются формулами (6.2.5) и (6.2.6), а SE= . Результат разности уi–
. Результат разности уi– =
= называют остатком от значения уi случайной переменной отклика или остаточной ошибкой и SE называют суммой квадратов остатков или суммой квадратов остаточных ошибок.
называют остатком от значения уi случайной переменной отклика или остаточной ошибкой и SE называют суммой квадратов остатков или суммой квадратов остаточных ошибок.
Так как знаменатель в выражении (6.2.16) принят равным n–2, то статистика s2 является несмещенным результатом оценки дисперсии s2. Это можно показать следующим образом. Сумму SE квадратов остатков можно записать в виде
SE = =
=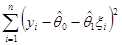 =
= =
=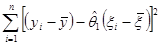
= –2
–2
 +
+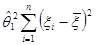
= –2
–2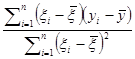
 +
+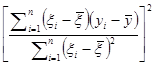
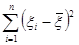
= –
–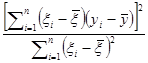
= –
– .
.
Усреднённое значение выборки переменных отклика принимает вид
 =
= =
= =q0+q1
=q0+q1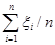 +
+ =q0+q1
=q0+q1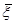 +
+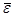
Математическое ожидание суммы  получается
получается
Е[ ]=Е[
]=Е[ ]=Е{
]=Е{ }
}
=Е{ }
}
=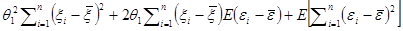
= ,
,
так как по аналогии с (5.1.2), имеем
 =
= –n
–n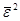
=eТIe–eТ(Е/n)e
=eТ(I–Е/n)e
и по теореме 5.2.1 математическое ожидание этой суммы
 =след[(I–Е/n)( s2I)]+е1Т(I–Е/n)е1
=след[(I–Е/n)( s2I)]+е1Т(I–Е/n)е1
=s2след(I–Е/n)+е2(1Т1–1Т11Т1/n) [так как Е=11Т]
=s2(n–n/n)+е2(n–n2/n) [так как 1Т1=n]
=s2(n–1)+0.
На основе выражения (3.2.4) можно получить Е( )=D(
)=D( )+[Е(
)+[Е( )]2=
)]2=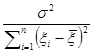 +q12. Следовательно, математическое ожидание суммы SE
+q12. Следовательно, математическое ожидание суммы SE
E(SE) = –
–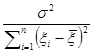
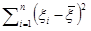 –q12
–q12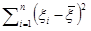
=(n–2)s2
и математическое ожидание статистики s2
E(s2)= =
= =s2, (6.2.17)
=s2, (6.2.17)
что и указывает на несмещённость статистики s2.
Интуитивно, в выражении (6.2.16) делителем взята разность n–2 вместо n–1, как в формуле (1.4.3) выборочной дисперсии, так как функция модели Е(уi) =q0+q1xi имеет два оцениваемых параметра и поэтому оценка ожидаемого значения E(уi) должна быть лучше, чем усреднённого  . Таким образом, можно ожидать, что SE=
. Таким образом, можно ожидать, что SE= меньше суммы
меньше суммы  . В самом деле, используя формулы (6.2.5) и (6.2.6), можно записать числитель выражения (6.2.16) в виде
. В самом деле, используя формулы (6.2.5) и (6.2.6), можно записать числитель выражения (6.2.16) в виде
SE= =
=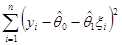
= =
=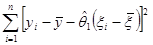
= –2
–2
 +
+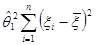
= –2
–2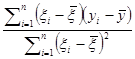
 +
+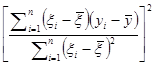
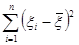
Лекция "20.1 Борьба за власть в руководстве страны после смерти И.В. Сталина" также может быть Вам полезна.
= –
–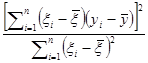 , (6.2.18)
, (6.2.18)
чем и подтверждается, что  меньше суммы
меньше суммы  .
.
Пример 6.2.2. Для данных примера 6.2.1 оценим дисперсию по формуле (6.2.16)
s2= =2,6149х104.
=2,6149х104.
□
Оценка дисперсии по формуле (6.2.16) зависит от числа параметров модели. Но если в эксперименте поставлены повторные опыты, то есть опыты при одних и тех же значениях переменной x, то можно оценить дисперсию независимо от числа параметров модели. Такая оценка дисперсии получена в конце следующего раздела, но вначале рассмотрим проверку гипотез о параметрах модели.





















