Математические ожидания и дисперсии квадратичных форм
5.2. Математические ожидания и дисперсии квадратичных форм
Рассмотрим сначала математическое ожидание квадратичной формы yТAy. При этом заметим, что квадратичная форма yТAy не является линейной функцией вектора у и её математическое ожидание E(yТAy)≠E(yТ)AE(у).
Теорема 5.2.1. Если вектор у случайных переменных имеет вектор y их средних и ковариационную матрицу S, а матрица А некоторых числовых значений симметричная, то
E(yТAy)=след(AS)+yТAy. (5.2.1)
Доказательство: В силу (3.3.8), имеем S=E(yyТ)–yyТ, что можно записать в виде
E(yyТ)=S+yyТ. (5.2.2)
Так как квадратичная форма yТAy является скалярным числом, то сама квадратичная форма равна её следу [Searle (1971) cтр. 54]. Таким образом, имеем
E(yТAy) =E[след(yТAy)]
=E[след(AyyТ)] [в силу (П.11.2)]
Рекомендуемые материалы
=след(E[AyyТ]) [в силу (3.3.5)]
=след(AE[yyТ]) [в силу (3.3.4)]
=след(A[S+yyТ]) [в силу (5.2.2)]
=след(AS+AyyТ)
=след(AS)+след(yТAy)] [в силу (П.11.1)]
=след(AS)+yТAy.
□
Пример 5.2.1. Применяя теорему 5.2.1, найдём математическое ожидание вычисляемой по формуле (1.4.3) выборочной дисперсии
s2= . (5.2.3)
. (5.2.3)
В силу (5.1.2), числитель выражения (5.2.3) можно записать в виде
 =yТ(I–Е/n)y,
=yТ(I–Е/n)y,
где уТ= [y1, y2,..., уn]. Если переменные y1, y2,..., уn, значения которых являются элементами вектора у, распределены независимо с общими средним y и дисперсией s2, то вектор у имеет математическое ожидание Е(у)=[y, y,..., y]Т=y1 и ковариационную матрицу C(у)=s2I. Таким образом, для применения формулы (5.2.1) имеем A=I–Е/n, S=s2I и y=y1. Следовательно, математическое ожидание числителя в (5.2.3) имеет вид
E =след[(I–Е/n)( s2I)]+y1Т(I–Е/n)y1
=след[(I–Е/n)( s2I)]+y1Т(I–Е/n)y1
=s2след(I–Е/n)+y2(1Т1–1Т11Т1/n) [так как Е=11Т]
=s2(n–n/n)+y2(n–n2/n) [так как 1Т1=n]
=s2(n–1)+0.
Отсюда математическое ожидание дисперсии выборки
Е(s2)= =
= = s2. (5.2.4)
= s2. (5.2.4)
□
В теореме 5.2.1 не предполагается, что вектор у случайных переменных имеет распределение по нормальному закону. Это предположение также может не делаться и для нахождения дисперсии квадратичной формы по формуле с использованием общих вторых, третьих и четвёртых моментов случайных переменных [Себер (1980) стр. 24]. Однако в статистическом линейном моделировании в основном имеют дело со случайными переменными, распределёнными по нормальному закону. Поэтому в следующих теоремах предполагается нормальность их распределений для получения функции, производящей моменты распределения квадратичной формы yТAy, и её дисперсии D(yТAy).
Теорема 5.2.2. Если вектор у имеет нормальное распределение Nn(y, S), то функцией, производящей моменты распределения квадратичной формы q=yТAy, является
Mq(t)=[det(I–2tAS)]–1/2exp{–yT[I–(I–2tAS)–1]S–1y/2}. (5.2.5)
Доказательство: Напомним, что матрицу А квадратичной формы можно считать симметричной [Boik (2011) cтр.142].
По определению функции, производящей моменты распределения переменной q, и по определению математического ожидания получаем,
Mq(t) =E[exp(tyТAy)]
= exp(tyTAy)k1exp[–(y–y)TS–1(y–y)/2]dy1dy2...dyn
exp(tyTAy)k1exp[–(y–y)TS–1(y–y)/2]dy1dy2...dyn
=k1 exp[tyTAy–(yTS–1y–yTS–1y–yTS–1y+yTS–1y)/2]dy1dy2...dyn
exp[tyTAy–(yTS–1y–yTS–1y–yTS–1y+yTS–1y)/2]dy1dy2...dyn
где k1=(2p)–n/2[det(S)]–1/2. В этом выражении преобразуем показатель степени экспоненты следующим образом
tyTAy–(yTS–1y–2yTS–1y+yTS–1y)/2=–(yTS–1y–2yTS–1y+yTS–1y–2tyTAy)/2
=–[yT(S–1–2tA)y–2yTS–1y+yTS–1y)/2
=–[yT(S–1–2tA)y–2yT(S–1–2tA)(S–1–2tA)–1S–1y+yTS–1y)/2
Теперь, принимая m=(S–1–2tA)–1S–1y, получаем
tyTAy–(yTS–1y–2yTS–1y+yTS–1y)/2=–[yT(S–1–2tA)y–2yT(S–1–2tA)m+ yTS–1y]/2
и, прибавляя и вычитая в правой части mT(S–1–2tA)m, она получается
=–[yT(S–1–2tA)y–mT(S–1–2tA)y–yT(S–1–2tA)m+mT(S–1–2tA)m–mT(S–1–2tA)m+ yTS–1y]/2
Вводя промежуточное обозначение B=S–1–2tA, выражение правой части преобразуем следующим образом
=–[yTBy–mTBy–yTBm+mTBm–mT(S–1–2tA)m+yTS–1y]/2
=–[(yTB–mTB)y–(yTB–mTB)m–mT(S–1–2tA)m+yTS–1y]/2
=–[(yTB–mTB)(y–m)–mT(S–1–2tA)m+yTS–1y]/2
=–[(y–m)TB(y–m)–mT(S–1–2tA)m+ yTS–1y]/2
=–[(y–m)T(S–1–2tA)(y–m)–mT(S–1–2tA)m+ yTS–1y]/2
и, так как m=(S–1–2tA)–1S–1y, то имеем
=–[(y–m)T(S–1–2tA)(y–m)–yTS–1(S–1–2tA)–1(S–1–2tA)(S–1–2tA)–1S–1y+ yTS–1y]/2
=–[(y–m)T(S–1–2tA)(y–m)–yTS–1(S–1–2tA)–1S–1y+ yTS–1y]/2
=–[(y–m)T(S–1–2tA)(y–m)–yTS–1(I–2tAS)–1y+ yTS–1y]/2
=–[(y–m)T(S–1–2tA)(y–m)]/2+[yTS–1(I–2tAS)–1y–yTS–1y]/2
=–(y–m)T(S–1–2tA)(y–m)/2–yTS–1[I–(I–2tAS)–1]y/2.
В результате получаем
Mq(t) =E[exp(tyТAy)]
=exp{–yTS–1[I–(I–2tAS)–1]y/2}k1 exp[–(y–m)T(S–1–2tA)(y–m)/2]dy1dy2...dyn.
exp[–(y–m)T(S–1–2tA)(y–m)/2]dy1dy2...dyn.
Далее, умножая правую часть на [det(S–1–2tA)]–1/2[det(S–1–2tA)–1]–1/2=1 и подставляя вместо k1 его выражение, получаем
Mq(t) =[det(S–1–2tA)]–1/2[det(S)]–1/2exp{–yTS–1[I–(I–2tAS)–1]y/2}
 [det(S–1–2tA)–1]–1/2(2p)–n/2exp[–(y–m)T(S–1–2tA)(y–m)/2]dy1dy2...dyn
[det(S–1–2tA)–1]–1/2(2p)–n/2exp[–(y–m)T(S–1–2tA)(y–m)/2]dy1dy2...dyn
=[det(I–2tAS)]–1/2exp{–yTS–1[I–(I–2tAS)–1]y/2},
так как функция [det(S–1–2tA)–1]–1/2(2p)–n/2exp[–(y–m)T(S–1–2tA)(y–m)/2] под интегралом представляет собой функцию плотности вероятности распределения вектора у, имеющего вектор m математических ожиданий и дисперсионную матрицу (S–1–2tA)–1. Кратный интеграл этой функции равен единице. Заметим, что абсолютная величина |t| должна быть достаточно малой, чтобы матрица (S–1–2tA) была положительно определённой. То есть при любом ненулевом векторе х=y–m квадратичная форма должна быть хT(S–1–2tA)х>0 или хTS–1х>2tхTAх. Следовательно необходимо чтобы t<(хTS–1х)/(2хTAх).
□
Так как переменная q имеет функцию Mq(t), производящую моменты её распределения, то её распределение полностью определено и можно найти его моменты на основе функции Mq(t) [Hogg с соавт. (2013) стр.61]. Существование функции Mq(t) на интервале –h<t<h изменения t означает, что при t=0 существуют производные функции Mq(t) всех порядков. Теорема дифференциального и интегрального исчисления позволяет также менять порядок дифференцирования и интегрирования. А так как переменная q непрерывная, то
dMq(t)/dt= =
= =
= .
.
При t=0 имеем dMq(t)/dt|t=0=Е(q)=q. Вторая производная функции Mq(t) имеет вид
d2Mq(t)/dt2= ,
,
так что d2Mq(t)/dt2|t=0=Е(q2). Таким образом, дисперсия D(q) равна
sq2=Е(q2)–q 2=d2Mq(t)/dt2|t=0–[dMq(t)/dt|t=0]2.
Это выражение может использоваться для нахождения дисперсии квадратичной формы.
Другое описание распределения даётся функцией Kq(t), производящей кумулянты или полуинварианты, и получаемой взятием натурального логарифма от функции, производящей моменты распределения переменной q, то есть,
Kq(t)=ln[Mq(t)].
Для получения дисперсии квадратичной формы q=yТAy необходимо чтобы вектор у имел нормальное распределение. Формула для получения произвольного кумулянта порядка r квадратичной формы имеет вид [Searle (1971) стр. 55]
Kr(уTAу)=2r–1(r–1)![след(AS)r+ryTA(SA)r–1y].
По этой формуле при r=2 находится дисперсия квадратичной формы. В следующей теореме доказывается, что дисперсия квадратичной формы от нормального вектора может быть найдена в результате оценки второй производной её кумулянта при t=0.
Теорема 5.2.3. Если случайный вектор у имеет нормальное распределение Nп(y, S), то дисперсия квадратичной формы yТAy находится по формуле
D(yТAy)=2след[(AS)2]+4yTASAy. (5.2.6)
Доказательство: [Rencher, Schaalje (2008) стр.109] Дисперсия случайной переменной q=yТAy может быть получена оценкой второй производной натурального логарифма функции Mq(t), производящей моменты её распределения, при t=0. Если Kq(t)=ln[Mq(t)], то
d[Kq(t)]/dt={d[Mq(t)]/dt}/Mq(t) и d2[Kq(t)]/dt2={d2[Mq(t)]/dt2}/Mq(t)–[{d[Mq(t)]/dt}/Mq(t)]2.
Так как Mq(0)=1, то d2[Kq(t)]/dt2|t=0=d2[M(t)]/dt2|t=0–[d[M(t)]/dt|t=0]2=sq2.
Введём обозначение C=I–2tAS. Тогда выражение (5.2.5) можно записать в виде
Mq(t)=[det(C)]–1/2exp[–yT(I–C–1)S–1y/2].
Возмём натуральный логарифм от этого выражения и обозначим его Kq(t)
Kq(t)=ln[Mq(t)]=– ln[det(C)]–yT(I–C–1)S–1y/2.
ln[det(C)]–yT(I–C–1)S–1y/2.
Для его дифференцирования воспользуемся теоремами о производных обратных матриц и определителей, данных в приложении (П.14.7). Первая производная Kq'(t) по t имеет вид
Kq'(t)=–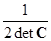
 – yTC–1
– yTC–1 C–1S–1y/2
C–1S–1y/2
Используя цепное правило, продифференцируем Kq'(t) второй раз по t чтобы получить
Kq''(t)=
 –
–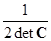
 +
+ yTC–1
yTC–1 C–1
C–1 C–1S–1y
C–1S–1y
– yTC–1
yTC–1 C–1S–1y+
C–1S–1y+ yTC–1
yTC–1 C–1
C–1 C–1S–1y
C–1S–1y
=
 –
–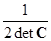
 –
– yTC–1
yTC–1 C–1S–1y+yT
C–1S–1y+yT C–1S–1y.
C–1S–1y.
Полезное выражение определителя det(C) можно найти с использованием (П.12.14). Так, если собственными значениями матрицы AS являются li (i=1, 2, ..., n), то получаем
det(C)=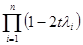
=1–2t +4t2
+4t2 –…+(–1)n2ntnl1 l2… ln.
–…+(–1)n2ntnl1 l2… ln.
Тогда
d[det(C)]/dt=–2 +8t
+8t + члены более высокого порядка от t
+ члены более высокого порядка от t
и
d2[det(C)]/dt2=8 + члены более высокого порядка от t.
+ члены более высокого порядка от t.
Оценивая эти выражения при t=0, получаем det(C)=1,
d[det(C)]/dt|t=0=–2 =–2след(AS)
=–2след(AS)
и
d2[det(C)]/dt2|t=0=8 .
.
При t=0 верно также, что C=I, C–1=I, dC/dt|t=0=2AS и d2C/dt2|t=0=O. Следовательно,
Kq''(0)=2[след(AS)]2–4 +0+4yTASAy
+0+4yTASAy
=2{[след(AS)]2–2 }+4yTASAy.
}+4yTASAy.
Так как матрица AS имеет собственные значения l1, l2,..., lп, то, в силу (П.12.15), след(AS)= [Searle (1982) стр. 278]. Тогда
[Searle (1982) стр. 278]. Тогда
[след(AS)]2= +2
+2 =след[(AS)2]+2
=след[(AS)2]+2 ,
,
где, в силу (П.12.6), след[(AS)2]= . И окончательно получаем
. И окончательно получаем
Kq''(0)=D(yТAy)=2след[(AS)2]+4yTASAy.
□
Рассмотрим теперь ковариацию C(у, yTAy) вектора у и квадратичной формы yTAy. Чтобы прояснить смысл выражения C(у, yTAy) обозначим yTAy опять одной случайной переменной q. Тогда C(у, q) является вектором столбцом, содержащим ковариации каждой переменной уi вектора у с переменной q
C(у, q)=Е{[y–E(y)][q–E(q)]}= . (5.2.7)
. (5.2.7)
[С другой стороны, C(q, у) будет вектором строкой.] Выражение для вектора ковариаций C(у, yTAy) дается в следующей теореме.
Теорема 5.2.4. Если вектор у случайных переменных имеет нормальное распределение Nn(y, S), то ковариация его с квадратичной формой yTAy определяется выражением
C(у, yTAy)=2SAy. (5.2.8)
Доказательство: По данному выражением (5.2.7) определению ковариации имеем
C(у, yTAy) =E{[у–Е(у)][yTAy–E(yTAy)]}.
Применяя теорему 5.2.1 для нахождения E(yTAy), это выражение становится
C(у, yTAy) =E{(у–y)[yTAy–след(AS)–yTAy]}.
Если записать квадратичную форму yTAy с использованием разности векторов y–y в виде
yTAy=(y–y+y)TA(y–y+y)
=(y–y)TA(y–y)+(y–y)TAy+yTA(y–y)+yTAy
=(y–y)TA(y–y)+2(y–y)TAy+yTAy,
то получаем выражение для искомой ковариации
C(у, yTAy)=E{(y–y)[(y–y)TA(y–y)+2(y–y)TAy–след(AS)]} (5.2.9)
=E[(y–y)(y–y)TA(y–y)]+2E[(y–y)(y–y)TAy]–E[(y–y)след(AS)]
=E[(y–y)(y–y)TA(y–y)]+2E[(y–y)(y–y)T]Ay–след(AS)E[y–y]
=0+2SAy–0.
Первое слагаемое в правой части равно 0 потому, что все третьи центральные моменты многомерного нормального распределения равны нулю. Это легко проверить, взяв тетью производную по t от правой части выражения (4.4.3). Результаты для двух других членов не зависят от нормальности распределения и для второго члена
E[(y–y)(y–y)T]=S, а для третьего члена E[y–y]=0.
□
Следствие 1. Пусть В – матрица некоторых числовых значений размеров kхп. Тогда
C(By, yTAy)=2BSAy. (5.2.10)
Доказательство: По определению
C(By, yTAy)=E{[Bу–Е(Bу)][yTAy–E(yTAy)]}
=E{B[у–Е(у)][yTAy–E(yTAy)]}
=BE{[у–Е(у)][yTAy–E(yTAy)]}
=BC(у, yTAy)
=2BSAy.
□
Для разделённого вектора v= случайных переменных билинейная форма xTAy определена выражением (П.2.26). Её математическое ожидание даётся в следующей теореме.
случайных переменных билинейная форма xTAy определена выражением (П.2.26). Её математическое ожидание даётся в следующей теореме.
Теорема 5.2.5. Пусть v= - разделённый вектор случайных переменных, чей вектор средних и матрица ковариаций даны также соответственно разделёнными
- разделённый вектор случайных переменных, чей вектор средних и матрица ковариаций даны также соответственно разделёнными
E(v)=E =
= и Syx=C
и Syx=C =
= ,
,
где вектор у размеров пх1, вектор х размеров qх1 и матрица Syx размеров пхq. Пусть А - матрица некоторых числовых значений размеров qхп, тогда математическое ожидание билинейной формы определяется выражением
E(xTAy)=след(ASyx)+xTAy. (5.2.11)
Доказательство: Аналогично доказательству теоремы 5.2.1. Ковариационная матрица векторов у и х имеет вид Syx=E[(y–y)(х–x)T], а математическое ожидание Е(ухT) =Syx+yxT. Последнее можно получить, если матрицу ухT записать в виде
ухT=yxT+(y–y)xT+y(хT– xT)+(y–y)(хT– xT)
и найти её математическое ожидание. Далее,
E(xTAy)=E[след(xTAy)]=E[след(AyxT)]
=след(E[AyxT])=след(AE[yxT])
=след(A[Syx+yxT])=след(ASyx+AyxT)
=след(ASyx)+след(AyxT)=след(ASyx)+след(xTAy)
=след(ASyx)+xTAy.
□
Пример 5.2.2. Для оценки ковариации популяций значений случайных переменных х и у, данной выражением (3.2.9) в виде sxy=E[(х–x)(у–y)], используем выборочную ковариацию
sxy= , (5.2.12)
, (5.2.12)
где (x1, y1), (x2, y2), ..., (xn, yn) - случайная выборка из двух популяций со средними x и y, дисперсиями sx2 и sy2 и ковариацией sxy. Выражение (5.2.12) можно записать в виде
sxy= =хT(I–E/n)y/(n–1), (5.2.13)
=хT(I–E/n)y/(n–1), (5.2.13)
где хT=[x1, x2,..., xn] и уT=[y1, y2,..., yn]. Поскольку при i≠j пара (xi, yi) не зависит от (xj, yj), то вектор v= имеет вектор средних и матрицу ковариаций соответственно
имеет вектор средних и матрицу ковариаций соответственно
E =
= =
= и С
и С =
= =
= ,
,
В лекции "6 Формула Ньютона-Лейбница" также много полезной информации.
где каждая единичная матрица I размеров пхп. Таким образом, для применения выражения (5.2.11), имеем A=I–Е/n, Syx=sxyI, x=x1 и y=y1. Отсюда
E[xT(I–Е/n)y]=след[(I–Е/n)sxyI]+x1T(I–Е/n)y1
=sxyслед(I–Е/n)+xy(1T1–1T11T1/n)
=sxy(n–1)+0
и поэтому
E(sxy)= =
= =sxy. (5.2.14)
=sxy. (5.2.14)





















