Распределения хи-квадрат

5.3. Распределения хи-квадрат

Перед знакомством с нецентральным распределением хи-квадрат c² вспомним рассмотренное в главе 1 центральное распределение c². Простейший вектор z^Т=[z₁, z₂, ..., z_n] независимых случайных переменных имеет стандартное нормальное распределение N_n(0, I). Сумма квадратов этих переменных

=z^Tz                                                     (5.3.1)

по определению имеет распределение c²(n), то есть, сама сумма квадратов n независимых и распределённых по стандартному нормальному закону случайных переменных является случайной переменной, имеющей центральное распределение c² с n степенями свободы.

Выражения для среднего, дисперсии и функции, производящей моменты случайной переменной, имеющей распределение c², приведены в следующей теореме.

Теорема 5.3.1. Если случайная переменная u=z^Tz имеет распределение c²(n), то

Е(u)=n,                                                          (5.3.2)

D(u)=2n,                                                        (5.3.3)

М_u(t)=(1–2t)^–n/2.                                             (5.3.4)

Рекомендуемые материалы

Доказательство: Так как u - квадратичная форма z^TIz, то Е(u), D(u) и М_u(t) могут быть получены путем применения соответственно теорем 5.2.1, 5.2.3 и 5.2.2 следующим образом:

E(z^TIz)=след(I)+0^ТI0=n,

D(z^TIz)=2след(I)+40^TI0=2n,

M_u(t)=[det(I–2tI)]^–1/2exp{–0^T[I–(I–2tI)^–1]I^–10/2}

={det[(1–2t)I]}^–1/2=(1–2t)^–n/2,

так как определитель det[(1–2t)I]=(1–2t)ⁿ, где п – ранг матрицы I.

□

Функция плотности вероятности распределения c²(n) имеет вид [Johnson c соавт. (1995) Vol.1, стр. 416]

р_хи-кв.(u)=,           при u ≥0,

где Г(п/2) - гамма-функция. Показанный на Рис. 5.3.1 синей кривой график функции плотности вероятности распределения c²(6) асимметричен, но с увеличением числа степеней свободы асимметрия становится меньше и при n >50 распределение c² принимает форму приблизительно нормального.

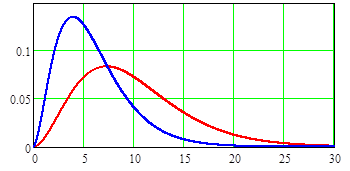
Рис. 5.3.1. Графики функций плотности вероятности распределений хи-квадрат: синий - центрального c²(n) при п=6 и красный - нецентрального c²(n, g) при п=6 и g=4.

Из рисунка видно, что случайная переменная, имеющая центральное распределение c², принимает только неотрицательные значения. Такие переменные используются для проверки гипотез о дисперсиях или стандартных отклонениях. Конкретное распределение c² определяется единственным параметром – положительным числом степеней свободы.

Теперь допустим, что переменные у₁, у₂, ..., у_n распределены независимо по нормальному закону N(y_i, 1), так что составленный из них вектор у имеет распределение N_n(y, I), где y^Т=[y₁, y₂,..., y_n]. В этом случае сумма =y^Тy не имеет распределения c². Однако, в силу (5.3.1), сумма квадратов разностей =(у–y)^Т(у–y) имеет распределение c²(n), так как переменная (у_i–y_i) имеет стандартное нормальное распределение N(0, 1).

Распределение случайной переменной v==y^Тy, в которой вектор у состоит из независимых и имеющих нормальное распределение N(y_i, 1) случайных переменных у₁, у₂, ..., у_n, называется нецентральным распределением c² и обозначается c²(n, g). Параметр g не центральности может определяться в виде

g ==y^Тy/2.                                                  (5.3.5)

Заметим, что математическое ожидание переменной v= больше математического ожидания переменной u=. Так, математическое ожидание переменной u

E[]====n,

а математическое ожидание переменной v

E[]=E(y^ТIy)=след(I)+y^ТIy  [по теореме 5.2.1]

=n+y^Тy=n+2g,

где g дано выражением (5.3.5).

Функцию плотности вероятности нецентрального распределения c²(n, g) можно представить в виде суммы функций плотности вероятности для центрального распределения c²(n) [Gendron (2015)] в виде

р_v(v)=exp[–(γ+v)/2].

График функции плотности вероятности нецентрального распределения c²(n, g) показан на Рис.5.3.1 красной кривой. При его расчёте с использованием программы Mathcad 13 в качестве бесконечности для суммы бралось число 145, так как при больших числах программа даёт ошибку, что получается число большее 10³⁰⁷, которое является бесконечно большим для этой программы.

Выражения для среднего, дисперсии и функции, производящей моменты случайной переменной, имеющей нецентральное распределение c², приведены в следующей теореме.

Теорема 5.3.2. Если вектор у имеет нормальное распределение N(y, I) и случайная переменная v=y^Тy имеет нецентральное распределение c²(n, g), то

Е(v)=n+2g,                                                                (5.3.6)

D(v)=2n+8g,                                                              (5.3.7)

M_v(t)=(1–2t)^–n/2exp{–g [1–(1–2t)^–1]}.                        (5.3.8)

Доказательство: Для получения выражения (5.3.6) найдём среднее E(y^ТIy) по теореме 5.2.1 и считая А=S=I,

Е(v)=E(y^ТIy)=след(I)+y^ТIy

=n+y^Тy=n+2g,                      [так как след(I)=п]

где g определено выражением (5.3.5).

Для получения выражения (5.3.7) найдём дисперсию D(y^ТIy), используя теорему 5.2.3 и принимая А=S=I,

D(v)=D(y^ТIy)=2след(I)+4y^TIy=2n+8g.

Для получения выражения (5.3.8) используем теорему 5.2.2

M_v(t)=[det(I–2tI)]^–1/2exp{–y^T[I–(I–2tI)^–1]I^–1y/2}

=(1–2t)^–n/2exp{–y^T[I–(I–2tI)^–1]I^–1y/2}     [так как [det(I–2tI)]^–1/2=(1–2t)^–n/2]

=(1–2t)^–n/2exp{–y^T[1–(1–2t)^–1]y/2}         [так как I=I^–1]

=(1–2t)^–n/2exp{–g[1–(1–2t)^–1]}.

□

Следствие 1. Если g=0 (что соответствует y=0), то Е(v), D(v) и M_v(t) теоремы 5.3.2 сводятся к Е(u), D(u) и М_u(t) центрального распределения c² теоремы 5.3.1. Таким образом,

c²(n, 0)=c²(n).                                                           (5.3.9)

□

Распределение c² обладает аддитивным свойством. Это показано в следующей теореме.

Теорема 5.3.3. Если случайные переменные v₁, v₂, ..., v_k распределены независимо и каждая имеет распределение c²(n_i, g_i) (i=1, 2, ..., k), то их сумма

 имеет распределение c²(,).                    (5.3.10)

Доказательство: Так как переменные v₁, v₂, ..., v_k распределены независимо, то функция, производящая моменты суммарной переменной v= имеет вид

М_v(t)=E[exp(t)]=E[exp(tv₁)exp(tv₂)…exp(tv_k)]

Если Вам понравилась эта лекция, то понравится и эта - Особенности культуры Древнего Египта.

=E[exp(tv₁)]E[exp(tv₂)]…E[exp(tv_k)]

==exp{–g_i[1–(1–2t)^–1]}

=(1–2t)^Sini/2exp{–[1–(1–2t)^–1] S_ig_i}.

Поэтому, в силу (5.3.8), сумма  имеет распределение c²(,).

□

Следствие 1. Если случайные переменные u₁, u₂, ..., u_п распределены независимо и каждая имеет распределение c²(n_i), то сумма  имеет распределение c²().