Функция плотности вероятности одномерного распределения
Глава 4 Многомерное нормальное распределение
При получении статистических выводов часто полагается, что представляющий интерес вектор случайных переменных имеет многомерное нормальное распределение. Однако перед выводом функции плотности вероятности многомерного нормального распределения и анализом её свойств рассмотрим сначала одномерное нормальное распределение.
4.1. Функция плотности вероятности одномерного распределения
Стандартное нормальное распределение
Получение стандартного нормального распределения основано на применении теоремы о центральном пределе. Центральная предельная теорема доказывает в частности важный факт, что, если у1, у2, ..., уп – значения случайной выборки из выборочного пространства с любым распределением, имеющим конечную дисперсию s2>0 и среднее y, то случайная переменная  (
( – y)/s сходится по распределению к нормированной случайной переменной z, имеющей стандартное нормальное распределение [Hogg c соавт. (2013) стр.307]. Эта переменная распределена по нормальному закону N(0, 1) и её функция плотности вероятности имеет вид
– y)/s сходится по распределению к нормированной случайной переменной z, имеющей стандартное нормальное распределение [Hogg c соавт. (2013) стр.307]. Эта переменная распределена по нормальному закону N(0, 1) и её функция плотности вероятности имеет вид
g(z)= ,
,
= exp(–z2/2) при –∞<z<∞. (4.1.1)
exp(–z2/2) при –∞<z<∞. (4.1.1)
Для нахождения моментов распределения случайной переменной используется производящая моменты функция, получаемая двусторонним преобразованием Лапласа. Пусть для случайной переменной z существует ожидаемое значение её функции exp(tz), в которой t - скалярная переменная, изменяющаяся в диапазоне –h<t<h для некоторого числа h >0. Функцией, производящей моменты распределения случайной переменной z, является Мz(t)=Е[exp(tz)]. Для распределённой по нормальному закону переменной z она может быть получена путём следующих преобразований [Hogg c соавт. (2013) стр.169]:
E[exp(tz)]= =
=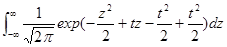
Рекомендуемые материалы
= =
=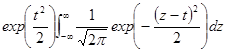
= .
.
В последнем интеграле сделана замена переменной z на w=z–t. При изменении значений переменной z от –∞ до +∞, интеграл функции (4.1.1) равен единице, поэтому и при замене переменной этот интеграл остаётся равным единице
 =1.
=1.
Следовательно, при изменении t в диапазоне –∞<t <∞, функция, производящая моменты распределения переменной z, имеет вид
Мz(t)=exp(t2/2). (4.1.2)
Первая и вторая производные этой функции по t равны соответственно t exp(t2/2) и exp(t2/2)+t2exp(t2/2). При t=0 эти производные принимают значения 0 и 1, которые для переменной z являются её средним и дисперсией.
Произвольное нормальное распределение
Непрерывную случайную переменную (у), распределённую по нормальному закону с произвольными средним y и дисперсией s2, можно получить из имеющей стандартное нормальное распределение переменной z, используя линейное преобразование
у=sz+y, (4.1.3)
где s>0.
Найдем функцию f(y) плотности вероятности переменной (у) на основе данной выражением (4.1.1) функции g(z) плотности вероятности стандартного нормального распределения. Для непрерывно возрастающей или убывающей функции (4.1.3) зависимости случайной переменной (у) от z существует непрерывная производная dy/dz. Необходимо найти функцию f(y) плотности вероятности распределения переменной (у). Для этого нужно изучить представляющее эту функцию отношение
 при Dy→0,
при Dy→0,
где Pr(y≤y<y+Dy) - вероятность попадания значения случайной переменной (у) в интервал величиной Dy.
При монотонности функции (4.1.3) на отрезке, где распределена переменная z, производная dy/dz будет положительная или отрицательная и, где она положительная,
Рr(у≤y<у+Dy)=Pr[z≤z<z+Dy/(dy/dz)]
с точностью до величин порядка малости выше, чем dz и dy [Линник (1962) стр.52]. Но для малых d имеем Рr(z≤z<z+d)=g(z)d с точностью до величин порядка малости выше d, что может быть записано так:
Pr(z≤z<z+d)≈g(z)d.
Отсюда
Pr[z≤z<z+Dy/(dy/dz)]≈g(z)dy/(dy/dz)
Таким образом
Рr(у≤y<у+Dy)≈ Dy.
Dy.
Следовательно, при стремящемся к нулю Dy, переменная (y) имеет функцию плотности вероятности
f(у)= .
.
Для случая отрицательной производной имеем f(у)=– , так что в общем случае получаем
, так что в общем случае получаем
f(у)= , (4.1.4)
, (4.1.4)
где |dy/dz| - абсолютная величина производной dy/dz.
Функция g(z) даётся выражением (4.1.1), а взятие производной от функции (4.1.3) по z даёт |dy/dz|=s. Таким образом, заменяя в функции g(z) переменную z получаемым из (4.1.3) её выражением z=(у–y)/s, функция плотности вероятности переменной (у), распределенной по нормальному закону в диапазоне –∞<у<∞, принимает вид
f(у)= =g
=g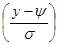
 ,
,
= exp
exp , (4.1.5)
, (4.1.5)
где Е(у)=y и D(у)=s2. Когда случайная переменная (у) имеет функцию (4.1.5) плотности вероятности, то она распределена по нормальному закону N(y, s2).
Для получения функции Му(t), производящей моменты распределения переменной (у), используем выражение (4.1.3) и функцию Мz(t), производящую моменты распределения переменной z. В результате имеем
Му(t)=E[exp(tу)]=E[exp{t(sz+y)}]
=exp(yt)E[exp(tsz)]
Рекомендуем посмотреть лекцию "17 - Периферическая и вегетативная нервная система".
=exp(yt)exp(s2t2/2) [в силу (4.1.2)]
=exp(yt+s2t2/2), (4.1.6)
при –∞<t <∞. Таким образом, переменная (у) распределена по нормальному закону N(y, s2), если и только если переменная z=(у–y)/s имеет стандартное нормальное распределение N(0, 1).
Пример 4.1. Если переменная (у) имеет производящую моменты функцию вида
Му(t)=exp(2t+32t2),
то она имеет нормальное распределение со средним y =2 и дисперсией s2=64, то есть N(2, 64). При этом случайная переменная z=(у–2)/8 имеет стандартное нормальное распределение N(0, 1).






















