Числовые ряды

Лекция 6.

Ряды в ТФКП

Большая часть теорем из теории рядов ТФКП доказывается  аналогично соответствующим теоремам из теории рядов действительных переменных.

Числовые ряды.

Числовой ряд  называется сходящимся, если сходится последовательность его частичных сумм  или .

Теорема. Для того чтобы ряд , где , сходился, необходимо и достаточно, чтобы сходились ряды из действительных и мнимых частей , .

Доказательство следует из теоремы лекции 2 относительно эквивалентности сходимости последовательности  сходимости последовательностей действительных и мнимых частей .

Следствие. Если ряд или ряд расходятся, то ряд расходится.

Рекомендуемые материалы

Доказательство (от противного) – проведите сами.

Замечание. Эта теорема как раз и «перекидывает мостик» между изученными ранее рядами действительной переменной и рядами комплексной переменной.

Критерий Коши. Для  того чтобы числовой ряд сходился, необходимо и достаточно, чтобы .

Доказательство.

Ещё посмотрите лекцию "ЛОМОНОСОВ Михаил Васильевич" по этой теме.

Необходимость. Если ряд  сходится, то ряды , сходятся. Следовательно, для них выполняется критерий Коши. Тогда. .

Выбирая,получим.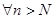

Достаточность. Пусть. Тогда, так как , то для рядов , выполнен критерий Коши. Следовательно, они сходятся. Тогда, по доказанной теореме ряд  сходится.

Теорема. Если ряд  сходится, то ряд  сходится (если ряд сходится абсолютно, то он сходится).

Доказательство. Ряд  – знакоположительный числовой ряд, так как  - неотрицательное действительное число. Так как  сходится и , то по первому признаку сравнения знакоположительных числовых рядов ряд  сходится. Аналогично, так как , то по первому признаку сравнения ряд  сходится. Поскольку ряды , сходятся абсолютно, то они сходятся. Тогда и ряд сходится.

Пример. Ряд  сходится, так как по признаку Лейбница сходятся ряды из действительных и мнимых частей.