Предел числовой последовательности. Сформулировать признак сходимости монотонной последовательности

Предел числовой последовательности. Сформулировать признак сходимости монотонной последовательности. Доказать теорему о единственности предела.

Число а называется пределом числовой последовательности  при  если для любого Е>0 существует натуральное число N(E), такое, что для любых n>N(E) выполняется условие , записывают .

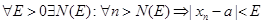
Числовая последовательность  монотонно не убывает (не возрастает) при  , если для   выполнено .

Если Вам понравилась эта лекция, то понравится и эта - Лекция 8.

     Признак: если числовая последовательность  при  , монотонно не убывает (не возрастает) и ограничена сверху (снизу) числом A (B), тогда она сходится и её предел не больше, чем A (не меньше, чем B)

Если последовательность , при  имеет конечный предел, то он единственный .

Доказательство: Пусть  имеет 2 предела a и b при . Пусть для определённости a>b .

;

.

N=max(N₁;N₂) 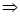 эти неравенства выполняются одновременно, чего быть не может, т.к. по определению E окрестность точки а содержит все члены последовательности, и E окрестность точки b содержит все члены последовательности 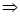 все члены не могут быть одновременно в 2 окрестностях, т.к. они не пересекаются.