Постановка задачи анализа объектов с распределенными параметрами

Постановка задачи анализа объектов с распределенными параметрами.

Постановка задачи. Математические модели на микроуровне, называемым распределенными, представлены дифференциальными уравнениями в частных производных вместе с краевыми условиями. Проектирование многих технических объектов связано с необходимостью анализа непрерывных физических процессов, математическим описанием которых являются дифференциальные уравнения в частных производных. Примером тому служат современные летательные аппараты, при проектировании и расчете которых широко используется анализ подобных моделей.

Рассмотрим примеры уравнений, составляющих основу моделей объектов на микроуровне. Первая важная задача проектирования летательного аппарата - определение прочности узлов и элементов конструкции при различных видах нагружения. Поэтому исследование напряженного состояния деталей конструкции и связанные с ним расчеты на прочность относятся к наиболее ответственным в самолетостроении.

Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается дифференциальными уравнениями различного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения

                                     (1.1),

где х, у, z - пространственные координаты;  - искомая непрерывная функция; К_х, К_у, K_z - коэффициенты; Q - внешнее воздействие.

В двухмерном случае при К_х=К_у=1 уравнение (1.1) сводится к уравнению, описывающему напряженное состояние, возникающее в поперечном сечении упругого однородного стержня под воздействием крутящего момента М:

,                                                           (1.2)

Рекомендуемые материалы

где Е - модуль сдвига материала стержня;  - угол закручивания на единицу длины, а функция  - функция, связанная с напряжениями сдвига  и  уравнениями

;                                                                (1.3)

В (1.2) в явном виде не входит крутящий момент, связанный с искомой функцией напряжения  уравнением , где S - площадь рассматриваемого сечения.

Вторая важная задача проектирования летательного аппарата - изучение его аэродинамических свойств. Решение этой задачи связано с исследованием процессов обтекания газом поверхностей произвольной формы. Наиболее общими уравнениями, описывающими этот процесс, являются уравнения Навье-Стокса, которые в декартовой системе координат имеют вид:

;

;               (1.4)

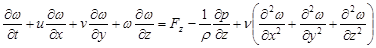
где и, ,  - проекции вектора скорости; F_х, F_y, F_z - проекции вектора силы на оси координат;  - плотность; р - давление;  ( - коэффициент вязкости).

Примечание. Система уравнений (1.4) незамкнутая, для решения ее следует доопределить с помощью уравнения неразрывности, которое в декартовой системе координат имеет вид:

,                                  (1.5)

,                                      где t - время.

Третья задача проектирования летательных аппаратов - расчет тепловых режимов работы деталей и узлов конструкции. Одним из основных аспектов задачи является определение температурных полей, имеющих место в конструкциях.

Примечание. Знание температурных полей необходимо для вычисления количества теплоты, подводимой к телу или отводимой от него. Кроме того, температурные поля влияют на распределение напряжений в конструкциях. Это обстоятельство особенно важно учитывать при проектировании вращающихся элементов летательных аппаратов.

Температурное поле в сплошной среде описывается уравнением теплопроводности. Последнее может быть получено из уравнения (1.1), если под функцией  понимать температуру Т, а под коэффициентом К - коэффициент теплопроводности . В двухмерном случае при условии, что коэффициенты теплопроводности  и  по соответствующим направлениям не зависят от координат, стационарное уравнение теплопроводности имеет вид

,                                                 (1.6)

Способы соединения двух компьютеров - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

где Q - источник теплоты внутри тела, который считается положительным, если теплота подводится к телу.

Сформулированные выше задачи - типичные для многих областей техники. Так, задачу исследования механических напряжений, возникающих в конструкциях, необходимо решать при проектировании мостов, арок, опор электропередачи и т. д. Рост быстроходности и удельной мощности тепловых двигателей вызывает необходимость более тщательного, чем ранее, исследования проблем механической прочности и тепловых режимов работы их деталей. Аналогичные проблемы возникают в автомобиле- и турбиностроении. Проектирование дамб, плотин, дренажных и оросительных каналов невозможно без тщательного анализа течения грунтовых вод. Последняя задача является частным случаем сформулированной выше задачи о течении жидкостей и газов. В градостроительстве при проектировании системы водоснабжения городов необходим анализ течения грунтовых вод.

Анализ течения жидкого или газообразного теплоносителя на основе уравнений Навье-Стокса проводится при проектировании ядерных реакторов. Кроме того, особо важная роль при проектировании ядерных установок отводится расчету тепловыделяющей системы, математической моделью (ММ) которой является нестационарное уравнение теплопроводности. В этом случае в уравнении (1.6) дополнительно появляется член, описывающий изменение искомого температурного поля во времени. При анализе тепловых процессов в тепловыделяющих элементах (ТВЭЛах), например в высокотемпературных газоохлаждаемых реакторах, уравнение теплопроводности удобнее записывать в сферических координатах в виде

                                                         (1.7)

где С_р - удельная теплоемкость материала ТВЭЛов; R - удельная ядерная мощность.