Краевые условия
Краевые условия.
Уравнения (1.2), (1.4), (1.6), (1.7) имеют множество решений. Для получения единственного решения необходимо задавать краевые условия (сведения об искомых непрерывных функциях на границах рассматриваемых областей - граничные условия, а в случае нестационарных задач - значения этих же функций в начальный момент времени - начальные условия). Исходное дифференциальное уравнение в частных производных вместе с краевыми условиями носит название дифференциальной краевой задачи и представляет собой ММ исследуемого объекта.
Граничные условия в краевых задачах могут задаваться различными способами. На границе рассматриваемой области можно задать:
а. значение искомой функции;
б. значения производных по пространственным координатам от искомой функции;
в. уравнение баланса потоков.
В случаях а-в говорят о граничных условиях первого, второго и третьего рода соответственно.
Для уравнений теплопроводности (1.6) и (1.7) чаще задают граничные условия первого и третьего рода. Другими словами, на границе с рассматриваемой областью задаются либо температура Т(х)=Т(с), либо условия теплообмена с внешней средой. При этом если на границе области имеет место конвективный теплообмен, то граничное условие третьего рода записывается в виде
(1.8)
Рекомендуемые материалы
где 
- коэффициент теплообмена, в общем случае являющийся функцией температуры; 
— температура окружающей, среды.
Обратите внимание на лекцию "2 Функции конфликтов".
Если на границе задан поток 
теплоты, то граничное условие
(1.9)
где поток считается положительным, если теплота отводится от рассматриваемого объекта.
Поток теплоты и конвективный теплообмен не могут задаваться одновременно на одном и том же участке границы. В частном случае, когда граница теплоизолирована, т. е. конвективный теплообмен отсутствует и поток теплоты равен нулю, имеет место граничное условие второго рода:
и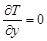 
Граничные условия для уравнений Навье-Стокса также могут быть весьма разнообразными. Например, в задаче об обтекании вязкой жидкостью или газом поверхности произвольной формы обычно задаются граничные условия первого рода, причем на границе необходимо задавать значения компонент вектора скорости, плотность и давление.
