Замена дифференциального оператора разностным аналогом

Замена дифференциального оператора разностным аналогом.

Эту процедуру легко проиллюстрировать на следующем простом примере. Пусть непрерывная функция , определенная на отрезке (рис. 1, а), описывается дифференциальным уравнением

                                                                   (1)

где А - константа; задано также граничное условие  и при дискретизации области была построена сетка с постоянным шагом h.

Заменим дифференциальный оператор  разностным:

                                                      (2)

Где  - правая разностная производная.

Подставив (2) в (1), получим разностное уравнение

                                      (3)

Рекомендуемые материалы

Умножив (3) на h и полагая последовательность х=0, h, 2h, …, перейдем к системе алгебраических уравнений:

                                           (4)

Решая (4) относительно сеточной функции, найдем таблицу значений, аппроксимирующую решение краевой задачи (1). При уменьшении шага h сетка становится все «гуще», а таблица значений сеточной функции - все подробнее. При неограниченном стремлении шага к нулю можно было бы получить значение искомой функции в каждой точке области. Но, в реальных случаях степень приближения к точному решению ограничивается рядом факторов, важнейшим из которых является размерность результирующей системы уравнений (4).

Для аппроксимации дифференциального оператора разностным кроме (2) часто пользуются выражением:

                                                     (5)

Где  - левая разностная производная.

Кроме того, для аппроксимации , можно воспользоваться любой линейной комбинацией (2)-(5), т.е.

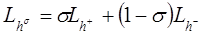
Где  - любая вещественная константа.

При  дифференциальный оператор  аппроксимируется центральной разностной производной.

                                             (6)

Подставив (6) в (1), получим другой разностный аналог краевой задачи (1):

.

Удобным геометрическим изображением схем построения разностных производных являются шаблоны.

На рис. 2 приведены шаблоны, соответствующие правой (рис. 2, а), левой (рис.2, б) и центральной (рис. 2, в) разностным производным.

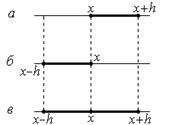
Рис. 2. Примеры шаблонов в одномерной области, соответствующих разностным производным: а – правой, б – левой, в – центральной.

При переходе от дифференциальной краевой задачи к разностной необходимо также аппроксимировать граничные условия. В рассмотренном примере (1) граничные условия при использовании (2) можно аппроксимировать точно:

                                                                                (7)

Совокупность разностного уравнения и разностных краевых условий называется разностной схемой краевой задачи.

В нашем примере уравнения (3) и (7) являются разностной схемой краевой задачи (1).

Кажущаяся простота построения разностной схемы в рассмотренном примере обманчива. В реальных задачах при построении разностных схем возникают проблемы. При исследовании разностных схем даже простых линейных задач часто выясняется, что разностная схема дает решение, не сходящееся при измельчении сетки к точному решению дифференциальной задачи. Поэтому построение сходящейся разностной схемы – центральный и наиболее сложный вопрос МКР.

Понятие сходимости разностной схемы тесно связано с понятиями точности и устойчивости.

Пусть точное значение непрерывной функции в узле с координатой x=x_h равно , а полученное значение точной функции в том же узле . Если погрешность  стремится к нулю при стремлении к нулю шага h и имеет k-й порядок относительного шага, то принято говорить, что разностная схема имеет k-й порядок точности в n-м узле.

Аналогично для определения порядка аппроксимации вычисляют погрешность между точным  и приближенным  значениями производной в n-м узле: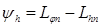  

Лекция "32 Русская культура XVIII века" также может быть Вам полезна.

При этом порядок погрешности  относительно шага впадает с порядком аппроксимации дифференциального  разностным  оператором в n-м узле.

Для определения порядка точности многих практических разностных схем достаточно определить порядок аппроксимации дифференциального оператора разности, так как порядки точности и аппроксимации для них совпадают. Однако разностная схема, для которой такое подтверждение может быть доказано, должна обладать еще одним важным свойством - устойчивостью.

Устойчивая разностная схема - схема, в которой не происходит наращивания малых ошибок округления, допущенных на начальных стадиях решения.

Для многих краевых задач сходимость разностной схемы является следствием аппроксимации ею краевой задачи и устойчивости. При этом порядок сходимости относительно шага совпадает с порядком аппроксимации.

Для гладких неразрывных функций хорошо развит математический аппарат изучения аппроксимации и доказательства устойчивости разностных схем.

Необходимость исследования сходимости впервые построенной разностной схемы обусловливает тот факт, что основу программных реализаций в САПР составляют вполне конкретные, хорошо изученные для определенных задач разностные схемы.