Интеграл функции комплексного переменного

Интеграл функции комплексного переменного

Пусть на комплексной плоскости задана кривая L - кусочногладкая, конечная, ориентированная.

  

      

;

Рекомендуемые материалы

Опр.  - некоторая функция

, где .

Существование интеграла и методы его вычисления.

Утв1. Если ; u и v – непрерывные функции; дуга L – кусочно гладкая, то  соответствующие криволинейные интегралы и    .

Док-во:

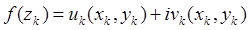
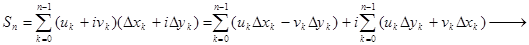
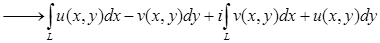
Утв2. Если , u  и v – непрерывные, дуга L – кусочно гладкая, то .

Док-во:

По Утв1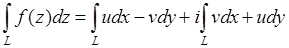

;

;

.

Свойства интеграла

1.

2.

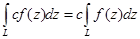
3.

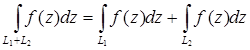
4. , где -L – обход дуги L в обратную сторону.

5. Если   , то , где -длина L.

Док-во:

 

длина хорды.

Замечание. Криволинейный интеграл существенно зависит от кривой.

Утв. .

Док-во:

.

След.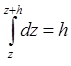

Ещё посмотрите лекцию "7 Моделирование и реинжиниринг процессов производства" по этой теме.

Утв.   где

Док-во:

  ()