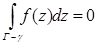Основная теорема Коши для многосвязной области

Основная теорема Коши для многосвязной области

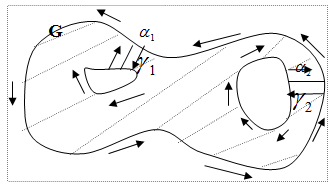
Теорема. Если G – многосвязаная область, связанная некоторыми контурами,  - аналитическая функция в G и на границе G, то интеграл по границе области G, проходимой по следующему правилу: при прохождении контура непосредственно примыкающая к нему область должна находится по левую руку (Г проходится по часовой стрелке, а -по стрелке) равен нулю.

Бесплатная лекция: "Водоудерживающая способность снега" также доступна.

Док-во:

1)  - аналитическая функция на границе, следовательно  - аналитическая в каждой точке границы  - аналитическая в каждой точке границы и в некоторой ее окрестности. Покроем границу окрестностями ее точек. Т.к. граница – компакт, то можно выделить конечное подпокрытие. Расширим область аналитичности, используя это покрытие граница погружена в область аналитичности.

2) Разрежем область G по - получим односвязную облость. Граница области G и линия разреза(граница новой области) лежат в области аналитичности функции .

3)

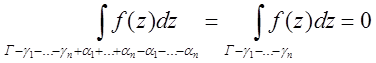
След. Если  лежит внутри Г,  - аналитическая в области между Г и  и на них, то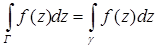

Док-во: