Соболевские пространства
§4. Соболевские пространства  и
и  .
.
Определим отображение
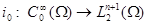
по правилу
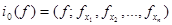
и пусть Im − образ этого отображения. Замыкание образа в пространстве
− образ этого отображения. Замыкание образа в пространстве  называется Соболевским пространством и обозначается
называется Соболевским пространством и обозначается
 .
.
Определим отображение
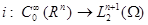
Рекомендуемые материалы
по правилу
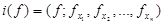
и пусть Im − образ этого отображения. Замыкание образа в пространстве
− образ этого отображения. Замыкание образа в пространстве  также называется Соболевским пространством и обозначается
также называется Соболевским пространством и обозначается  .
.
Лемма 1.
Пусть  . Тогда
. Тогда

 .
.
Итак, для доказательства леммы 1 достаточно установить равенство:
 . (1)
. (1)
Сначала мы предположим, что 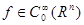 . Функцию
. Функцию  можно продолжить нулем за пределы
можно продолжить нулем за пределы  . Запишем соотношение (1) в виде:
. Запишем соотношение (1) в виде:
 . (2)
. (2)
Ограниченность носителя 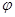 означает, что он лежит в достаточно большом кубе:
означает, что он лежит в достаточно большом кубе:  .
.
Поэтому (2) можно записать в эквивалентном виде:
 .
.
Записав n-кратный интеграл в виде повторного, будем иметь:
 . (3)
. (3)
Остается заметить, что для функции 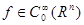
 ,
,
так, что 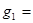
 и (3) совпадает с обычной формулой интегрирования по частям,
и (3) совпадает с обычной формулой интегрирования по частям,
поскольку  благодаря ограниченности носителя, то есть внеинтегральные члены нулевые.
благодаря ограниченности носителя, то есть внеинтегральные члены нулевые.
Пусть теперь  произвольный вектор. По определению, найдется последовательность
произвольный вектор. По определению, найдется последовательность  такая, что
такая, что  . Последнее равносильно тому, что
. Последнее равносильно тому, что  в
в  и
и  в
в  . По доказанному:
. По доказанному:
 .
.
Пользуясь непрерывностью скалярного произведения, переходя к пределу при  при фиксированной функции
при фиксированной функции 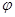
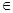
 , получим утверждение леммы 1 в общей ситуации.
, получим утверждение леммы 1 в общей ситуации.
Определение 1.
Пусть для функции 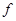
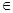
 существует функция
существует функция 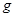
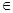
 , такая, что:
, такая, что:
 .
.
Тогда функцию 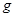 называют обобщенной производной функции
называют обобщенной производной функции 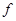 по переменной
по переменной  .
.
Пример. Функция 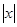
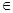
 имеет обобщенную производную sgn
имеет обобщенную производную sgn  . В самом деле:
. В самом деле:
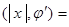

 .
.
Как следует из доказательства леммы 1, общая производная, если она лежит в  , является обобщенной производной.
, является обобщенной производной.
Лемма 2.
Если обобщенная производная существует, то она единственна.
Доказательство.
"4.6 Политика Просвещенного абсолютизма Екатерины II" - тут тоже много полезного для Вас.
Пусть  . Тогда
. Тогда  . Поскольку
. Поскольку  является плотным множеством в
является плотным множеством в  , то найдется последовательность
, то найдется последовательность  . Переходя к пределу получим
. Переходя к пределу получим  , или
, или  . Лемма доказана.
. Лемма доказана.
Теперь мы знаем, что вектор  однозначно восстанавливается по первой компоненте. Остальные компоненты
однозначно восстанавливается по первой компоненте. Остальные компоненты  являются обобщенными производными первой компоненты. Поэтому в дальнейшем под элементами
являются обобщенными производными первой компоненты. Поэтому в дальнейшем под элементами  будем понимать первые компоненты f вектора
будем понимать первые компоненты f вектора  .
.
Иногда приходится рассматривать пространство  , состоящее из функций f
, состоящее из функций f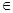
 , все первые обобщенные производные которых так же лежат в
, все первые обобщенные производные которых так же лежат в  . Очевидно
. Очевидно 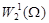
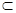
 .
.
Теорема.
Если область ограничена и имеет границу класса  , то
, то  =
= .
.
Доказательство теоремы громоздкое. [см.1]



















