Прямая сумма гильбертовых пространств
§3. Прямая сумма гильбертовых пространств.
Пусть 
гильбертовы пространства со скалярными произведениями 
соответственно. Тогда множество пар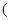 
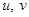
, где 
образует векторное пространство 
со сложением
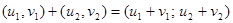
и умножением на число
.
После задания в скалярного произведения пар 
и 
по правилу
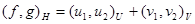
оно превращается в гильбертово пространство с нормой
.
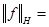
Рекомендуемые материалы
Если 
и 
были сепарабельными, то и будет сепарабельным. Сходимость 
последовательности в равносильна сходимости двух последовательностей 
и vn →v в пространствах и соответственно.
"6. Регистрация документов" - тут тоже много полезного для Вас.
Пространство Н называется прямой сумой гильбертовых пространств и и обозначается 
. По индукции можно определить прямую сумму любого конечного числа пространств. В частности, определены гильбертовы пространства 
.
Лемма (о непрерывности скалярного произведения).
Если и 
в гильбертовом пространстве , то 
при 
.
Доказательство.
.
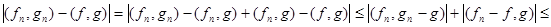
Здесь мы воспользовались ограниченностью 
для сходящейся последовательности.
