Линейные функционалы
§2. Линейные функционалы.
Задача2. Доказать, что в гильбертовом пространстве справедливо неравенство Коши-Буняковского  .
.
Определение 1.
Линейное отображение гильбертова пространства  в комплексные числа называется функционалом
в комплексные числа называется функционалом 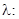
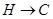
 .
.
Определение 2.
Функционал  на
на  называется непрерывным, если
называется непрерывным, если
 .
.
Определение 3.
Рекомендуемые материалы
Функционал  на
на  называется ограниченным, если
называется ограниченным, если
 .
. 
Теорема 1.
Линейный функционал непрерывен  ограничен.
ограничен.
Доказательство.
Пусть  ограничен. Возьмем
ограничен. Возьмем  и
и  . Тогда
. Тогда
 .
.
Непрерывность функционала установлена.
Если же функционал непрерывен, то берем  . Тогда существует
. Тогда существует  из определения непрерывности. Для произвольного
из определения непрерывности. Для произвольного  положим
положим
 .
.
Тогда  .
.
Отсюда  . Ограниченность установлена.
. Ограниченность установлена.
Пример1. В гильбертовом пространстве  для всякого
для всякого  определен линейный функционал
определен линейный функционал  по правилу
по правилу
 .
.
Ввиду неравенства Коши-Буняковского он является ограниченным (непрерывным)
 .
.
Ниже мы докажем теорему Рисса о том, что других линейных функционалов в гильбертовом пространстве нет.
Определение 4.
Ортогональным дополнением множества  в гильбертовом пространстве
в гильбертовом пространстве  называют множество
называют множество
 .
.
Определение 5.
Подмножество  гильбертова пространства
гильбертова пространства  называют линейным многообразием, если
называют линейным многообразием, если
 .
.
Определение 6.
Линейное многообразие  называется подпространством, если оно замкнуто.
называется подпространством, если оно замкнуто.
Пример2.  − подпространство в
− подпространство в  .
.
 − подпространство в
− подпространство в  .
.
Пример3.  − линейное многообразие в
− линейное многообразие в  , не являющееся подпространством, поскольку замыкание
, не являющееся подпространством, поскольку замыкание  .
.
Задача3. Доказать, что  − подпространство при любом
− подпространство при любом  .
.
Теорема 2.
Если  − подпространство в
− подпространство в  , то
, то 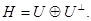
Напомню, что знак прямой суммы означает существование  единственных векторов
единственных векторов  таких, что
таких, что 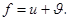
Теорема 3. (Теорема Рисса)
Для всякого линейного непрерывного функционала  в гильбертовом пространстве
в гильбертовом пространстве  найдется единственный вектор
найдется единственный вектор  такой, что
такой, что  .
.
Определение 7.
Ядром линейного функционала называется множество
ker  .
.
Лемма.
ker  является подпространством (сравни с задачей 3).
является подпространством (сравни с задачей 3).
Доказательство.
Если  ker
ker , то
, то  .
. Тем самым,
Тем самым,  ker
ker .
.
Покажем замкнутость ker . Если
. Если  ker
ker − сходящаяся к
− сходящаяся к  последовательность, то ввиду непрерывности
последовательность, то ввиду непрерывности  имеем
имеем 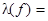
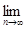
 ker
ker , что доказывает замкнутость ker
, что доказывает замкнутость ker . Лемма доказана.
. Лемма доказана.
Доказательство теоремы 3.
По теореме2 имеем  ker
ker
 ker
ker
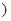 ┴. Докажем одномерность пространства
┴. Докажем одномерность пространства  ker
ker
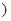 ┴. Пусть υ1,υ2
┴. Пусть υ1,υ2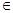
 ker
ker
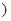 ┴. Тогда w=
┴. Тогда w=
 υ1
υ1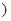 υ2
υ2 υ2
υ2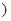 υ1
υ1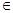
 ker
ker
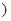 ┴. С другой стороны
┴. С другой стороны 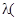 w
w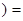
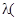
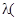 υ1
υ1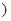 υ2
υ2 υ2
υ2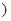 υ1
υ1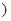 =
=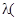 υ1
υ1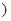
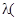 υ2
υ2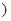
 υ2
υ2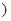
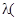 υ1
υ1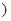
 , поэтому w
, поэтому w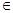 ker
ker  .
.
Отсюда (w,w) , то есть w
, то есть w − одномерность доказана.
− одномерность доказана.
Люди также интересуются этой лекцией: Ханство Абылая.
Пусть  единичный вектор из
единичный вектор из  ker
ker
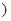 ┴. По теореме 2
┴. По теореме 2  имеем
имеем

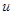
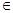 ker
ker 
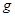
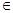
 ker
ker 
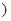 ┴
┴
 .
.
Тогда  .
.
Далее,  . Таким образом
. Таким образом
 , т.е. υ
, т.е. υ  .
.
Докажем единственность вектора υ. Если  ,
,  . Полагая
. Полагая  , установим
, установим  .
.





















