Гильбертовы пространства
§1. Гильбертовы пространства.
Евклидовы и гильбертовы пространства играют важную роль в теории дифференциальных уравнений с частными производными.
Определение 1.
Евклидовым пространством называется векторное пространство  над полем
над полем  , если в нем определено отображение
, если в нем определено отображение  , называемое скалярным произведением, удовлетворяющее аксиомам:
, называемое скалярным произведением, удовлетворяющее аксиомам:
1. 
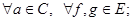
2. 
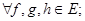
3. 
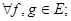
4. 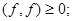
5.  .
.
Рекомендуемые материалы
Число 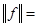
 называется нормой вектора
называется нормой вектора 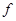 .
.
Последовательность векторов  называется фундаментальной, если
называется фундаментальной, если

 .
.
Последовательность векторов  называется сходящейся, если существует вектор
называется сходящейся, если существует вектор  такой, что числовая последовательность
такой, что числовая последовательность  .
.
Определение 2.
Евклидово пространство  называется гильбертовым, если в нем всякая фундаментальная последовательность сходится.
называется гильбертовым, если в нем всякая фундаментальная последовательность сходится.
Во многих случаях достаточно обходиться евклидовыми и гильбертовыми пространствами над полем  . В дальнейшем именно эти пространства мы будем иметь в виду. Если же потребуется пространство над полем
. В дальнейшем именно эти пространства мы будем иметь в виду. Если же потребуется пространство над полем  , то этот случай специально оговаривается.
, то этот случай специально оговаривается.
Пример1. Пространство  является гильбертовым пространством над полем
является гильбертовым пространством над полем  со скалярным произведением
со скалярным произведением
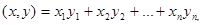
 .
.
Пример2. Пространство  2 состоит из последовательностей
2 состоит из последовательностей  , для которых
, для которых  <¥. Сложение последовательностей определяется, как в
<¥. Сложение последовательностей определяется, как в  ,
,
т.е. покоординатно. Скалярное произведение задается формулой:
 ,
,
 .
.
Нетрудно проверить, что  2 является гильбертовым пространством.
2 является гильбертовым пространством.
Пример3. Пространство непрерывных функций  является евклидовым пространством со скалярным произведением
является евклидовым пространством со скалярным произведением
 .
.
Но это пространство не является гильбертовым. Действительно, возьмем фундаментальную последовательность
 .
.
Легко видеть, что она “сходится ” к функции
 .
.
Но эта функция не принадлежит  !
!
Имея евклидово пространство, всегда можно “изготовить” гильбертово пространство. Процедура изготовления называется пополнением и состоит в следующем. Рассматривается множество  всех фундаментальных последовательностей в
всех фундаментальных последовательностей в  . На этом множестве вводится отношение эквивалентности.
. На этом множестве вводится отношение эквивалентности.
Две фундаментальные последовательности  называются эквивалентными, если объединенная последовательность
называются эквивалентными, если объединенная последовательность  , также является фундаментальной. Множество
, также является фундаментальной. Множество  классов эквивалентности по этому отношению и называется пополнением пространства
классов эквивалентности по этому отношению и называется пополнением пространства  .
.
Нетрудно доказать, что  будет гильбертовым пространством. В частности,
будет гильбертовым пространством. В частности,  , будет гильбертовым пространством.
, будет гильбертовым пространством.
Имея вектор  , можно изготовить постоянную фундаментальную последовательность
, можно изготовить постоянную фундаментальную последовательность  . Тем самым определено отображение
. Тем самым определено отображение
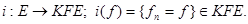
Нетрудно проверить, что  .
.
Однако работать непосредственно с  несколько тяжеловесно. Поэтому желательно иметь более “осязаемое” описание для
несколько тяжеловесно. Поэтому желательно иметь более “осязаемое” описание для  . К счастью,
. К счастью,
в случае  такое описание существует.
такое описание существует.
Пример4. Пространство  состоит из измеримых функций, для которых
состоит из измеримых функций, для которых
 .
.
Если определить отображение
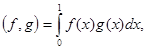
то оно не будет скалярным произведением  , поскольку существуют функции
, поскольку существуют функции 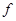
 , для которых
, для которых

 .
.
Такие функции называют равными нулю почти всюду.
Пространство равных нулю почти всюду функций обозначим Оп.в. Тогда фактор-пространство  /Оп.в. обозначают
/Оп.в. обозначают  .
. Оно будет гильбертовым пространством.
Оно будет гильбертовым пространством.  Доказательство сложное.
Доказательство сложное.
Здесь придется вспомнить, что элементами  являются классы эквивалентных функций.
являются классы эквивалентных функций.
Временно будем обозначать их так
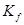
 .
.
Возникает вопрос: верна ли формула
 ?
?
Ответ да, верна, то есть при вычислении скалярного произведения можно брать любую функцию из класса эквивалентных функций. Для доказательства следует установить равенство:
 .
.
Имеем
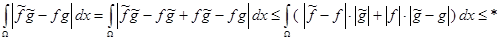
Хотя на множестве  не выполнена аксиома 5 скалярного произведения, тем не менее неравенство Коши-Буняковского остается справедливым
не выполнена аксиома 5 скалярного произведения, тем не менее неравенство Коши-Буняковского остается справедливым

Изоморфность гильбертовых пространств означает существование отображения  , которое взаимно однозначно и изометрично, т.е.
, которое взаимно однозначно и изометрично, т.е.  .
.
Теорема 1.
 (без доказательства).
(без доказательства).
Определение 3.
Областью в  называют открытое связное множество.
называют открытое связное множество.
Определение 4.
Носителем функции 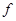 называют множество supp
называют множество supp .
.
Черта сверху означает замыкание множества.
Определение 5.
Пространство  (
( −область в
−область в  ) состоит из гладких функций с ограниченным носителем, лежащим в
) состоит из гладких функций с ограниченным носителем, лежащим в  :
:
 supp
supp  diam supp
diam supp .
.
Скалярное произведение
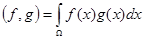
превращает  в евклидово пространство. Оно не гильбертово и его следует пополнить.
в евклидово пространство. Оно не гильбертово и его следует пополнить.
Теорема 2.
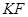
 .
.
Пространство  определяется точно также, как и
определяется точно также, как и  .
.
Определение 6.
Множество  называется всюду плотным в гильбертовом пространстве
называется всюду плотным в гильбертовом пространстве  , если
, если
 .
.
Определение 7.
Люди также интересуются этой лекцией: 13 Внешнеполитический курс Николая I.
Гильбертово пространство  называется сепарабельным, если в нем существует счетное всюду плотное множество.
называется сепарабельным, если в нем существует счетное всюду плотное множество.
Теорема 3.
Если область  ограничена, то многочлены с рациональными коэффициентами образуют счетное всюду плотное множество в
ограничена, то многочлены с рациональными коэффициентами образуют счетное всюду плотное множество в  .
.
Таким образом, из теоремы 3 следует, что  при ограниченной области
при ограниченной области
 является сепарабельным.
является сепарабельным.
Задача1. Пусть  − неограниченная область. Доказать, что
− неограниченная область. Доказать, что  − сепарабельно.
− сепарабельно.



















