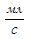Элементы гидродинамики

2. Элементы гидродинамики.

Кровь – несжимаемая жидкость. Во всяком случае, в диапазоне условий, в котором она функционирует, это бесспорно. Несжимаемость жидкости означает, что объем любой ее порции остается неизменным (DV = Const) в условиях повышения или понижения давления, но жидкость свободно принимает форму сосуда, трубы, в которых она находится.

2.1. Уравнение неразрывности.

Следствием несжимаемости жидкости является ее хорошо известное свойство: чем уже русло, тем больше скорость течения. Это свойство описывается следующим уравнением:

                      S₁ V₁ = S₂ V₂ ,    или         SV = Const                                         (1)

Здесь S – площадь поперечного сечения потока, V  - средняя скорость жидкости в этом сечении.

Уравнение (1) называется уравнением неразрывности. В порядке его обоснования и иллюстрации рассмотрим схему потока жидкости на рис.1, в его сечениях 1 и 2.

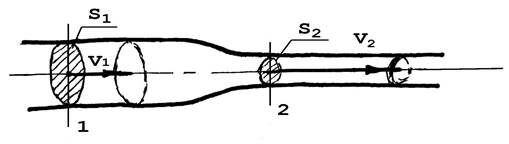                                                                                                                               Рис.1

Рекомендуемые материалы

За интервал времени Dt = 1с частицы жидкости, оказавшиеся в его начале, на заштрихованном сечении S₁, сместятся вправо на расстояние, равное скорости V₁. Объем цилиндрика S₁ V_{1 –} это объем жидкости, прошедшей через сечение S₁ за Dt = 1с. Точно такой же объем, но представленный сомножителями S₂ V₂, пройдет и через сечение 2, поскольку:

а) жидкость несжимаема,

б) поток не разветвлялся.

Величина Q = SV имеет размерность , имеет смысл количества жидкости, протекающей через поперечное сечение потока в единицу времени. В гемодинамике для системы кровообращения в целом, эта величина называется общим объемом кровотока. Для взрослого человека в спокойном его состоянии

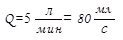
С помощью уравнения неразрывности увяжем значения скорости кровотока в аорте и в капиллярах. В спокойном состоянии человека скорость кровотока в аорте – порядка V₁ = 0,4 м/с. Измерения под микроскопом показывают, что скорость в капиллярах – V₂ = 0,5 мм/с = 5×10^-4 м/с. Эти значения отличаются друг от друга в 800 раз. Следовательно, если площадь сечения аорты S₁ = 4 см², то общая площадь поперечных сечений системы капилляров большого или малого круга кровообращения составляет     S₂ = 3200 см² = 3,2×10³ см².

Получив эти данные, оценим степень ветвления общего потока крови в системе капилляров. Диаметр капилляра d = 10 мкм = 0,01 мм = 10^{-3 см; следовательно, площадь его сечения} S = pd²/4 = 0,78×10^-6 см². Стало быть, кровь из аорты разветвляется в системе капилляров на штук. Такая фантастическая степень ветвления достигается поэтапно, в системе «артерии – артериолы – капилляры».

Можно прикинуть суммарную протяженность этих параллельно работающих капилляров. Принимая среднее значение их длины l = 0,7 мм, получаем суммарную протяженность капилляров:

L = Nl = 4,1×10⁹×0,7 = 2,9×10⁹ мм = 2,9×10⁶ м = 2900 км.

Этот результат следует удвоить: в системе кровообращения – две последовательные системы капилляров. Получаем, что общая протяженность всех капилляров нашего организма – порядка 5800 км.

Мы рассмотрели предельно  упрощенную расчетную схему, давшую впечатляющий, но – заниженный результат. Истинная общая протяженность всех капилляров нашего организма – порядка 100000 км, что достаточно, чтобы опоясать Землю 2,5 раза!

2.2. Уравнение Бернулли.

Уравнение Бернулли, знакомое Вам по средней школе, справедливо для стационарных потоков жидкости, в которой отсутствуют силы вязкого трения.

Стационарным называется режим течения, в котором значения скоростей жидкости во всех точках потока установились на неизменном уровне, т.е. постоянны во времени. Применительно к системе кровообращения, стационарным является течение крови в функционально основной части этой системы – во всей совокупности капиллярных сосудов. В них скорость V » 0,5 мм/с = Const. Во всей остальной части кровеносной системы течение крови нестационарно.

Кроме того, вся энергия, вносимая в систему сердечными сокращениями, постепенно расходуется на преодоление трения, а в уравнении Бернулли потери энергии не учитываются. Тем не менее, уравнение Бернулли представляет определенный интерес, если применять его для близких сечений кровеносной системы и при этом подставлять в него усредненные по времени величины.

Уравнение Бернулли соответствует закону сохранения механической энергии при движении жидкости или газа и верно в той степени, в которой потери на трение малы. Оно имеет следующий вид:

p + rgh + rV²/2 = p₀ = Const                                              (2)    

Здесь p₀ – величина, называемая полным давлением. В левой части равенства – слагаемые этого полного давления, сумма которых в идеальном случае одинакова во всех сечениях потока. Величина p – это давление, которое поток оказывает на стенки; его называют статическим давлением. Слагаемое rV²/2 называется динамическим давлением; оно на стенки не передается, и может быть обнаружено и измерено только если трубку для измерения этого давления поместить в поток и непременно так, чтобы эта трубка была направлена и открыта навстречу потоку. Слагаемое rgh соответствует тому вкладу в общее давление p₀, которое создается участками потока, приподнятыми на высоту h, если таковые имеются. r - плотность жидкости; V – ее скорость.

С помощью уравнения Бернулли проанализируем качественно ряд ситуаций в системе кровообращения.

l Рассмотрим статическое давление в последовательной гидравлической линии, участки которой находятся на различной высоте. На схеме рис.2 – это сечения 1, 2 и 3.

Положим для простоты, что скорость жидкость V во всех сечениях одинакова. Уравнение Бернулли для сечений 1 и 2 запишется:

p₁ + rV²/2 + 0 = p₂ + rV²/2 + rgh₂

Отсюда, после сокращения динамических давлений, получаем:

p₂ = p₁ - rgh₂

Аналогично, для сечений 1 и 3:

p₁ = p₃ - rgh₃,

Отсюда следует, что

p₃ = p₁ + rgh₃

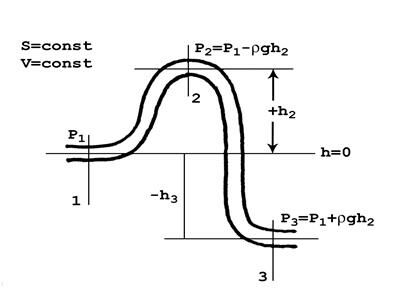Мы убедились, что статическое давление в приподнятых участках: p₂ < p₁, а в опущенных – наоборот, p₃ > p₁.

Рис. 3

Применительно к системе кровообращения, если p₁ – давление, создаваемое сердцем, работающим на высоте h = 0, то все, что находится выше этого уровня, имеет пониженное давление (а это, в частности, мозг), а все, что ниже (ноги, например) – давление выше, чем то, которое создает работающее сердце. Для мозга слагаемое rgh имеет величину порядка –30 мм рт. столба, а для ног – порядка +110 мм рт. столба. Система кровообращения имеет механизмы регулирования, вносящие поправки на снабжение кровью органов, находящихся в неравных условиях; об этом – в разделе 3. И все же:

А.) Наиболее полноценным является ночной сон в лежачем положении, а не в автобусных и самолетных креслах.

Б.) Знакомое многим ощущение тяжести в ногах после длительной ходьбы (отекание ног) снимается отдыхом в лежачем или полулежащем положении. В американской неприличной традиции – это ноги на столе.

l Слагаемое rgh полного давления крови становится особо актуальным в условиях экстремальных перегрузок, действующих на тело летчиков, космонавтов, автогонщиков. В условиях больших перегрузок система саморегулирования кровообращения оказывается далеко за пределами диапазона отклонений, на который она природно рассчитана. Техническое решение этой проблемы: располагать тело человека так, чтобы вектор   ускорения при перегрузках, заменяющий в этих условиях вектор ускорения свободного падения  , оказался сориентированным в направлении «грудь – спина», а никак не «голова – ноги». Направление «спина – грудь» неприемлемо: возникают большие проблемы с дыханием.

l Обсудим специфику действия динамического давления  rV²/2 в условиях организма. В целом, скорость движения крови в системе кровообращения невелика, и в спокойном состоянии динамическое давление составляет порядка 1% от полного. Однако при больших нагрузках скорость кровотока существенно возрастает, растет и доля динамического давления, достигая 30% и более.

Динамическая компонента давления энергетически не выгодна: какой смысл разгонять массы крови до больших скоростей, если все равно она должна будет затормозиться до скоростей движения в капиллярах? Рост скорости кровотока – это рост потерь на преодоление гидравлического сопротивления, а следовательно – рост нагрузки на сердце.

Непроизводительные расходы энергии оправданы в тех случаях, когда процессы обмена веществ должны быть интенсифицированы любой ценой, т.е. в экстремальных ситуациях.

l А теперь обсудим роль динамического давления при измерении артериального давления по методу Короткова. Воспользуемся схемой рис.1. Пусть 1 – сечение артерии перед манжетой, а сечение 2 – под манжетой.

В сечении 1 V₁ » 0; а давление P₁ – это максимальное давление крови в заторможенном потоке, которое мы хотим измерить как систолические.

Но в сечении 2 кровь, в момент засечки систолического давления прорывается через малый просвет артерии; V₂ ¹ 0, и появление сопутствующих этому шумов – сигнал к тому, чтобы засечь давление P₂; оно в манжете такое же, как в сосуде.

Но из уравнения Бернулли следует:

p₁ + 0 = p₂ + rV²/2

и следовательно, между давлением P₁, которое мы хотели бы измерить, и давлением P₂, которое мы фактически измеряем, есть некоторая разность:

p₁ – p₂ = rV²/2

Колебания стрелки манометра в такт с турбулентными шумами, которые прослушиваются на локтевом сгибе при «засечке» систолического давления, происходят в моменты появления и исчезновения разности (P₁ – P₂) в последней формуле. При этом максимальное давление крови в систоле – это тот максимум, который показывает колеблющаяся стрелка манометра.

Любопытная деталь: скорость кровотока, при которой он становится турбулентным (шумным), прорываясь в просвет артерии – порядка V₂ = 4 м/с; и тогда при плотности крови r » 1г/см³ = 10³ кг/м³ динамическое давление r₂V₂   = 8×10⁵ Па, что в пересчете на ртутный столб составляет 60 мм. Между тем размах колебаний стрелки манометра при фиксации систолического давления гораздо меньше. Так проявляется нестационарность потока крови, и в первую очередь нестационарность самих сосудов. Мы соприкоснулись с тем фактом, что требования стационарности потока действительно являются серьезными при строго количественном применении уравнения Бернулли.

l Уже упоминавшаяся в разделе 1 ситуация на входе в правое предсердие может быть прокомментирована с позиций уравнения Бернулли. Подчеркнем еще раз, что все измерения давления крови в кровеносной системе – это измерения давления, избыточного над атмосферным давлением. На входе в правое предсердие этот избыток становится равным нулю. Но кровь течет, а значит динамическое давление rV²/2 ¹ 0. Полное давление как сумма статического и динамического давлений:

р_полн = р_ст + rV²/2 = 0

Отсюда следует, что статическое давление вынуждено принимать отрицательные значения:

р_ст = -rV²/2

Это означает, что давление в таких венах – несколько ниже атмосферного, и при их повреждении возможна эмболия – попадание воздуха в полости сердца. На реальном сердце такое статическое давление, которое правильнее называть разрежением, составляет величину порядка р_ст = -3 мм рт. столба.

l В уравнении Бернулли (2) полному давлению р₀ соответствует тот результат, который достигается в ходе сокращений желудочков сердца. При этом левый и правый желудочки, работая синхронно, функционально разнесены на обслуживание двух последовательных участков единой замкнутой сети. Техническим аналогом той ситуации является любой нефте- или газопровод, вдоль линии которого функционируют подкачивающие насосные станции.

 Однако полное давление р₀, создаваемое этой системой из двух сердец, вместо того, чтобы оставаться постоянным, как это было бы в идеальном случае, постепенно снижается, и на подходах к правому предсердию, как уже отмечалось, имеем: р + rV²/2 + rgh = 0

Вся энергия, внесенная в систему за счет мышечных сокращений сердца, оказывается полностью израсходованной на преодоление сил трения, действию которых соответствует некоторый тепловой эффект, чрезвычайно слабый, учитывая, что мощность сердца – порядка 1,2 Вт.

Вся система кровообращения жизнеспособна, если сердце сокращается снова и снова.

Работа сердца за один цикл срабатывания:

DА = p×DV,

где DV ударный объем крови; p – максимальное давление, создаваемое на выходе левого желудочка в ходе его сокращения.

2.3. Вязкость жидкостей.

Свойство жидкостей, которое мы называем вязкостью, проявляется в том, что всякое движение, возбуждаемое в жидкости, вскоре прекращается. Вязким является мед, особенно загустевший.

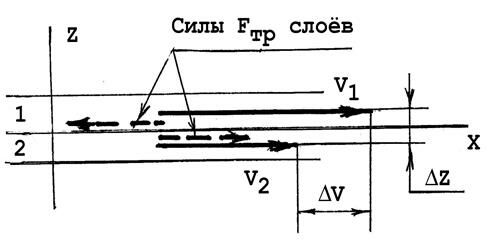
Вязкость жидкости можно обнаружить и изучать количественно, рассматривая взаимодействие слоев жидкости, имеющих различную скорость.

Экспериментально установлено, что сила трения, возникающая между слоями 1 и 2:

                                               (4)

здесь  - отношение, называемое градиентом скорости в направлении, перпендикулярном потоку жидкости. S – площадь соприкосновения слоев; на схеме не показана. h – коэффициент пропорциональности, зависящий от свойств жидкости, и называемый динамическим коэффициентом вязкости.

Примечания:

1. Конечным разностям DV и DZ и их отношению DV/DZ в более точном описании взаимодействия слоев следует предпочесть их аналог dV/dZ, имеющий математический смысл производной.

2. Производная  характеризует непостоянство скорости в направлении оси Z, перпендикулярной потоку. Кроме того, скорость непостоянна и в направлении оси потока X; с мерой непостоянства . Такие производные по различным направлениям в математике называются частными производными, и обозначаются ; .

Уравнение (4) можно сформулировать так: сила вязкого трения пропорциональна градиенту скорости в направлении, перпендикулярном потоку, и площади соприкосновения слоев, с коэффициентом пропорциональности – коэффициентом вязкости жидкости.

 Взаимодействие между слоями осуществляется возникающими парами сил. Любая из них соответствует уравнению (4). Эта пара сил действует так, чтобы способствовать выравниванию скоростей в слоях.

   Если в формуле (4) все величины будут иметь размерность основных единиц системы СИ, то единица вязкости h будет иметь размерность 1 Па×с. У различных жидкостей коэффициент вязкости весьма различен. Приведем примеры для знакомых жидкостей, взятых при Т = 20°С.

Вода – 1,002 мПа×с

Ацетон – 0,322 мПа×с

Глицерин – 1480 мПа×с

По особенностям коэффициента вязкости жидкости делятся на две категории:

А.) Ньютоновские

Б.) Неньютоновские

У ньютоновских жидкостей коэффициент вязкости зависит только от их температуры.

У неньютоновских – коэффициент вязкости зависит не только от температуры, но и от условий протекания: градиента скорости, размеров потока, давления в нем.

Ньютоновские жидкости имеют простые молекулы, или это молекулы низкомолекулярных органических соединений.

К неньютоновским относятся жидкости с протяженными молекулами высокополимеров, суспензии, эмульсии.

Кровь – неньютоновская жидкость, представляющая собой суспензию форменных элементов в белковом «растворителе» – плазме. Форменные элементы – эритроциты, лейкоциты, тромбоциты – составляют сообща 40-50% объема крови. Поэтому если вязкость плазмы – порядка 1,7 - 2,2 мПа×с, то вязкость крови в норме – 4 - 5 мПа×с. При движении крови в спокойном (ламинарном) потоке эритроциты выстраиваются своей длинной осью вдоль потока.

В неспокойном потоке такой строй эритроцитов нарушается, меняется и коэффициент вязкости.

Значения коэффициента вязкости крови в норме и при патологии могут отличаться в несколько раз. Если в номе это 4 - 5 мПа×с, то при отклонениях от нормы – это диапазон от 1,5 до 24 мПа×с. Следовательно, коэффициент вязкости может быть важным диагностическим показателем ее состояния..

Величина, обратная коэффициенту динамической вязкости, называется текучестью жидкости.

2.4. Режимы течения жидкостей.

Если в соседних слоях жидкости значения скорости близки дуг к другу, то такие слои сосуществуют очень мирно, течение в них –  ламинарное.

Положение существенно меняется, если в направлении, перпендикулярном потоку, перепады (градиенты) скоростей в соседних слоях оказываются велики. В этом случае на границах слоев возникают временные образования – вихри жидкости, и в целом течение жидкости становится неспокойным, неустойчивым. Такой режим течения называется турбулентным. Он сопровождается возникновением колебаний давления в жидкости, что приводит к появлению шумовых эффектов.

Появление турбулентных вихрей в потоке крови – это появление дополнительного вида движения в ней, на которые необходимы дополнительные затраты энергии работающего сердца.

Что касается градиентов скорости, возникающих в потоке жидкости, то здесь, не вдаваясь в частности, положение таково: чем больше средняя скорость движения жидкости (в кровеносном сосуде, в водопроводной трубе), тем больше и градиенты скорости в потоке. Изучение связи этих показателей с характеристиками жидкости – ее вязкостью и плотностью, привело к созданию безразмерного критерия – числа Рейнольдса, которое можно назвать индикатором режима течения жидкости.

                               (5)

Здесь r - плотность жидкости; h - динамическая вязкость; V – средняя скорость; d – диаметр трубы или сосуда, по которому течет жидкость.

В очень медленных потоках течение ламинарное, чему соответствуют малые значения числа Re. Чем больше средняя скорость V, тем больше становится и значение числа Re, особенно в крупных потоках с большим диаметром d. При некотором сочетании параметров, входящих в формулу (5), число Рейнольдса принимает критическое значение Re_кр, что соответствует тому факту, что спокойное ламинарное течение становится уже невозможным. Для различных жидкостей Re_кр различно. Так, для воды Re_кр = 2300. Для крови Re_кр = 970 ± 80. В сосуде диаметром 2,5 мм значение Re_кр достигается при скорости движения крови около 4 м/с.

Появление турбулентных вихрей, как уже отмечалось, приводит к нарушению «строя» эритроцитов, характерного для течения ламинарного. Эти нарушения «строя» отслеживаются и изменением величины электрического сопротивления крови: оно возрастает.

Отметим, что обратный переход жидкости от турбулентного течения к ламинарному происходит при Re < Re_кр. Это означает, что ламинарный режим течения легче разрушить, чем потом восстановить.

Разрушителями ламинарного течения жидкости при значениях Re < Re_кр могут оказаться резкие изломы, выступающие в поток элементы и прочие турбулизаторы, приводящие к срыву ламинарного течения. В кровеносных сосудах это могут быть склеротические бляшки на их стенках.

2.5. Формула Пуазейля.

В тонких длинных трубках с ламинарным режимом течения жидкости выполняется соотношение, полученное Пуазейлем и  Стоксом и известное как формула Пуазейля:

                      (6)

Здесь Q – объемный секундный расход жидкости; Dр – перепад давлений на трубке; l – длина трубки; r – ее радиус; h - коэффициент трения.

Формула фиксирует, прежде всего, причинно-следственную связь  Q ~ Dр: есть перепад давлений Dр – есть и течение жидкости; чем больше Dр, тем больше Q.

Аналогично обстоят дела с током электрическим: I ~Dj (или I ~ U); И здесь – такая же простая логика: есть разность потенциалов Dj (она же – напряжение U) на концах проводника – есть электрический ток I; чем больше Dj, тем больше I. Эта связь силы тока и напряжения известна как закон Ома для участка цепи , где R – электрическое сопротивление. По аналогии, величину, обратную дроби в формуле (6), называют гидравлическим сопротивлением:

             (7)

Аналогия гидравлического тока с электрическим оказалась достаточно глубокой. Сопротивление последовательных и параллельных цепей электрических и гидравлических описывается одними и теми же формулами. Сложноразветвленные гидравлические цепи легко моделируются аналогичными по структуре электрическими цепями, а их создание и исследование – гораздо проще, быстрее и дешевле, чем цепей гидравлических.

Для закона Ома и формулы Пуазейля характерно, что оба эти результата, каждый в своей области, являются приближенными. Однако с поправками и оговорками они широко используются на практике.

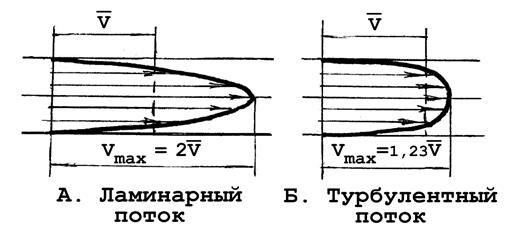В формуле гидравлического сопротивления особо выделяется множитель r⁴: влияние радиуса сосуда на гидравлическое сопротивление сосуда чрезвычайно сильное. Во многом это объясняется тем, что в ламинарных потоках распределение скорости жидкости по поперечному сечению очень неравномерное; оно описывается параболической кривой (рис. 4А), и получается, что наибольшая по площади периферийная часть сечения, примыкающая к стенкам, используется для переноса жидкости довольно-таки неэффективно; основная часть величины Q переносится в ядре потока.

       Рис. 4

При турбулентном течении распределение скоростей жидкости по поперечному сечению описывается логарифмической кривой, и является более близким к равномерному. В этом случае влияние радиуса сосуда на гидравлическое сопротивление будет описываться не множителем r⁴, а как-то по другому; например r^x, где х < 4 и определяется опытным путем. Но и в турбулентном варианте влияние радиуса сосуда на его гидравлическое сопротивление весьма сильное.

2. Оздоровление воздушной среды - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

В связи с этим, как объяснение, так и лечение гипертонической болезни замыкаются на сосуды, их гипертонус: зажатость, уменьшение радиуса, а значит – уменьшение их пропускной способности (увеличение гидравлического сопротивления). В этих условиях для обеспечения необходимого общего объема кровотока сердце вынуждено компенсировать рост гидравлического сопротивления ростом артериального давления.

При гипотонии ситуация обратная: тонус артериол понижен.

Величина гидравлического сопротивления сосудов сильно зависит от состояния стенок сосудов и от их эластичности. Эти показатели никак не учтены в формуле гидравлического сопротивления (7), но их влияние в полной мере проявляется при нарушениях в сосудистой системе, характерных для атеросклероза. Кроме того, при этом недуге могут иметь место изменения состава крови, ведущие к росту ее вязкости, а это – снова фактор роста гидравлического сопротивления X всех сосудов и системы в целом.

Гидравлическое сопротивление не системы в целом, но его значительной части – большого круга кровообращения, принято называть общим периферическим сопротивлением сосудов (ОПСС) и оценивать по приблизительной формуле:

                                                   ОПСС =                                                         

Здесь Q – общий объем кровотока;     - среднее артериальное давление. Как показатель нормы, ОПСС = 144 , при Q=5=80