Метод А.Н. Крылова для нахождения коэффициентов характеристического многочлена
2020-06-032021-03-09zzyxelСтудИзба
Метод А.Н. Крылова для нахождения коэффициентов характеристического многочлена.
Этот метод позволяет построить для заданной матрицы  характеристический многочлен
характеристический многочлен  , который можно записать в виде:
, который можно записать в виде:
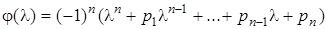
Согласно теореме Гамильтона-Кэли сама матрица  удовлетворяет характеристическому уравнению
удовлетворяет характеристическому уравнению  , а значит
, а значит  . Умножим это равенство на произвольный вектор
. Умножим это равенство на произвольный вектор  и получим
и получим  . Обозначив
. Обозначив  ,
,  , …,
, …,  , будем иметь
, будем иметь  . Это векторное равенство эквивалентно системе уравнений относительно коэффициентов характеристического многочлена
. Это векторное равенство эквивалентно системе уравнений относительно коэффициентов характеристического многочлена
 ,
,
где  - координаты вектора
- координаты вектора  . Решив эту систему каким-либо известным способом, получим коэффициенты характеристического многочлена
. Решив эту систему каким-либо известным способом, получим коэффициенты характеристического многочлена  . При неудачном выборе начального вектора
. При неудачном выборе начального вектора  рекомендуется выбрать другой вектор
рекомендуется выбрать другой вектор  и повторить процесс вычислений снова.
и повторить процесс вычислений снова.





















