Минимизация КНФ
Минимизация КНФ
Определение. Элементарная дизъюнкция u называется имплицентой булевой функции F , если  .
.
Например, элементарная дизъюнкция  является имплицентой функции
является имплицентой функции  .
.
Определение. Если никакая собственная часть  имплиценты u ( т.е.
имплиценты u ( т.е.  ) булевой функции F не является имплицентой F, то u называется простой имплицентой (т. е. если удаление из u хотя бы одного литерала нарушает условие
) булевой функции F не является имплицентой F, то u называется простой имплицентой (т. е. если удаление из u хотя бы одного литерала нарушает условие  , то u – простая имплицента).
, то u – простая имплицента).
Например,  – простая имплицента булевой функции
– простая имплицента булевой функции  , имплицента
, имплицента  не является простой для этой функции , так как
не является простой для этой функции , так как  (собственная часть имплиценты
(собственная часть имплиценты  ) является имплицентой функции F.
) является имплицентой функции F.
Определение. Конъюнкция всех простых имплицент булевой функции F называется сокращенной КНФ (СкКНФ) функции F.
Рекомендуемые материалы
Например,  – СкКНФ булевой функции
– СкКНФ булевой функции  . Отметим, что СкКНФ является единственной для конкретной булевой функции F.
. Отметим, что СкКНФ является единственной для конкретной булевой функции F.
Определение. КНФ булевой функции F, содержащая наименьшее число множителей среди всех КНФ, реализующих функцию F, называется кратчайшей КНФ (КрКНФ).
Например,  является также и КрКНФ этой же булевой функции F.
является также и КрКНФ этой же булевой функции F.
Вообще говоря, для заданной булевой функции F может существовать несколько различных по числу вхождений литералов КрКНФ.
Определение. КНФ булевой функции F, содержавшая наименьшее число вхождений литералов среди всех КНФ, реализующих функцию F, называется минимальной КНФ (МДНФ).
Отметим, что для заданной булевой функции F существует, вообще говоря, несколько МКНФ, отличающихся друг от друга числом слагаемых.
Более того, МКНФ не всегда совпадает с КрКНФ булевой функции n переменных F. Хотя для начальных значений n ( n = 2 или n = 3 ) МКНФ всегда совпадает с КрКНФ. Например,  является КрКНФ и МКНФ рассматриваемой функции F.
является КрКНФ и МКНФ рассматриваемой функции F.
Задача минимизации булевой функции  в классе КНФ формулируется следующим образом: требуется для булевой функции n переменных F построить КНФ с минимально возможным числом множителей (КрКНФ) или с минимально возможным числом вхождений литералов (МКНФ).
в классе КНФ формулируется следующим образом: требуется для булевой функции n переменных F построить КНФ с минимально возможным числом множителей (КрКНФ) или с минимально возможным числом вхождений литералов (МКНФ).
Также отметим, что задача минимизации булевых функций n переменных F в классе КНФ также как и задача минимизации булевых функций n переменных F в классе ДНФ является чрезвычайно громоздкой и ее трудоемкость с ростом n возрастает по экспоненциальному закону.
К настоящему времени разработано около 200 различных методов минимизации булевых функций в классе КНФ.
Пример. Составить по таблице истинности СКНФ булевой функции  и минимизировать ее, применяя законы склеивания.
и минимизировать ее, применяя законы склеивания.
Решение.
|
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
СКНФ будет иметь вид:  .
.
Минимизируем ее, применяя законы склеивания. Подчеркнем дизъюнкции, которые можно склеить. Очевидно, что это можно сделать различными способами, например:
 ,
,
 .
.
Выберем один из возможных вариантов склеивания, например  и минимизируем КНФ:
и минимизируем КНФ:
 .
.
Замечание. При минимизации КНФ достаточно часто (но не всегда!) удается получить лучшие результаты, если «нарастить» данную КНФ используя свойство идемпотентности дизъюнкции:  .
.
Например, в рассматриваемом примере третью, последнюю дизъюнкцию  можно было бы склеить со второй дизъюнкцией
можно было бы склеить со второй дизъюнкцией  . Добавив вторую дизъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации КНФ более короткое ее представление:
. Добавив вторую дизъюнкцию еще раз, мы не изменим саму булеву функцию, но получим в результате минимизации КНФ более короткое ее представление:

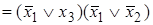 .
.
Ответ: F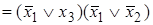
Пример. Составить СКНФ булевой функции, заданной вектором значений таблицы истинности w(F)=(00100111) и минимизировать ее, применяя законы склеивания.
Решение. Так как вектор значений заданной булевой функции имеет 8=23 разрядов, следовательно, булевой функции соответствует следующая таблица истинности:
|
|
|
| F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Вам также может быть полезна лекция "2. Горные предприятия".
СКНФ будет иметь вид:
 .
.
К сожалению, минимизировать ее, применяя законы склеивания, невозможно.
Ответ:  .
.