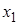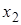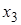Полиномиальное разложение булевых функций
Полиномиальное разложение булевых функций
Определение. Под полиномом булевой функции F понимается представление F посредством сложения по модулю два попарно различных элементарных конъюнкций. Иначе такое представление F называется полиномиальным разложением или полиномиальной нормальной формой (ПНФ) функции F.
Например, полиномом булевой функции F, заданной вектором значений таблицы истинности w(F)=(00100111), является следующее выражение  .
.
Число конъюнкций, образующих полином, называется длиной полинома, а максимальный ранг элементарной конъюнкции - степенью полинома.
В приведенном выше примере длина полинома функции F равна 3, а степень – 2.
Определение. Полином функции F, состоящий только из полных элементарных конъюнкций, называется совершенной ПНФ (СПНФ). По аналогии с СДНФ такое представление конкретной булевой функции F является единственным.
Рассмотрим на примерах построение СПНФ, используя преобразование СДНФ булевой функции.
Рекомендуемые материалы
Пример. Составить СПНФ булевой функции, заданной вектором значений таблицы истинности w(F)=(10010010).
Решение. Так как вектор значений заданной булевой функции имеет 8=23 разрядов, следовательно, булевой функции соответствует следующая таблица истинности:
|
|
|
| F |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
СДНФ данной булевой функции, построенная по таблице истинности будет иметь вид:  .
.
Заменим операцию дизъюнкции на операцию сложения по модулю два по формуле:  . При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (при построении СДНФ по таблице истинности это очевидно ― все наборы отличаются хотя бы по отрицанию одной переменной). Следовательно, СПНФ будет иметь вид:
. При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (при построении СДНФ по таблице истинности это очевидно ― все наборы отличаются хотя бы по отрицанию одной переменной). Следовательно, СПНФ будет иметь вид:
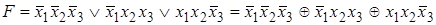 .
.
Ответ: 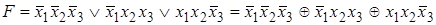
Пример. Составить СПНФ булевой функции, если СДНФ данной булевой функции, имеет вид:  .
.
Люди также интересуются этой лекцией: Тема 1. Элементы нейроцитологии.
Решение. Заменим операцию дизъюнкции на операцию сложения по модулю два по формуле:  . При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (при построении СДНФ по таблице истинности это очевидно ― все наборы отличаются хотя бы по отрицанию одной переменной). Следовательно, СПНФ будет иметь вид:
. При этом воспользуемся тем, что произведение (конъюнкция) любых полных дизъюнкций СДНФ всегда равно нулю (при построении СДНФ по таблице истинности это очевидно ― все наборы отличаются хотя бы по отрицанию одной переменной). Следовательно, СПНФ будет иметь вид:
 .
.
Полином F, содержащий наименьшее число слагаемых среди всех полиномов, реализующих функцию F, называется кратчайшей ПНФ (КрПНФ). Полином функции F, содержащий наименьшее число вхождений литералов, называется минимальной ПНФ.
Существует задача минимизации булевых функций в классе ПНФ, которая формулируется как задача нахождения для заданной булевой функции КрПНФ иди МПНФ. Такая задача также является весьма трудоемкой, и для ее решения разработано немало методов (отдельные из которых представляют собой соответствующую интерпретацию известных методов минимизации функций в классе ДНФ).
В следующем пункте настоящей методической разработки будет рассмотрено построение канонических поляризованных полиномов булевых функций (в частности, полинома Жегалкина), как наиболее часто применяемых при синтезе логических схем.