Простейшие задачи аналитической геометрии

§2. Простейшие задачи аналитической геометрии.

    В этом параграфе будут рассмотрены три задачи: вычисление координат вектора   по координатам точек  А  и  В,  вычисление длины отрезка  и  деление отрезка в данном отношении.

 1. Вычисление координат вектора  .

                               В                    Пусть − произвольный вектор пространства (рис.2). Точки  А'  

                            М                    и  В'  с координатами  А_х  и  В_х − проекции точек  А  и  В  на ось  ОХ.

          А                                       Координаты вектора равны его проекциям на координатные оси (§1).

                                                   Следовательно, его первая координата  равна  В_х − А_х  (гл.I ,§3,св.3).

         А'           М'    В'       ОХ    Аналогичный результат получается для остальных координатных

                   Рис.2                       осей. Таким образом:  .

Рекомендуемые материалы

2.  Вычисление длины отрезка.

  Так как длина отрезка  АВ (|AB|)  равна  , то |AB| =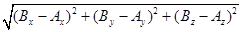

  (гл.1, §7).

2. Деление отрезка в данном отношении.

   Рассмотрим т.  (рис.2). Требуется определить число  , где АМ  и  МВ − величины направленных отрезков , называемое отношением, в котором т. М  делит

направленный отрезок . Из курса элементарной геометрии и полученных результатов имеем:   . Отсюда легко получаем координаты точки  М:

                         .

Люди также интересуются этой лекцией: 18. Итальянское возрождение.

Замечания.

1. Наиболее важным частным случаем является деление отрезка пополам:   

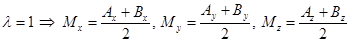
2. Полученный результат сохраняется для любого расположения точек, лежащих

на одной прямой. В случае, когда т. величина  λ  будет отрицательной.