Алгоритмны генерирования линий

АЛГОРИТМЫ ГЕНЕРИРОВАНИЯ ЛИНИЙ.

При формировании любой линии  предъявляются следующие очевидные  требования:

- линия должна начинаться и заканчиваться в заданных точках;

- контрастность и яркость вдоль всей длины формируемой линии должны быть одинаковыми и не зависеть от крутизны и длины линии;

- необходимо отражать характер линии (отрезки прямой должны быть прямыми, формируемые дуги должны иметь форму дуги и т. д.);

- формирование отдельных точек должно выполняться с минимальными затратами времени, так как количество точек, так правило, достаточно велико.

Не все перечисленные требования могут быть выполнены.

Из-за принципиальных особенностей средств графического ввода-вывода, носитель, на котором формируется или с которого считывается графическая информация, рассматривается в виде матрицы дискретных элементов, называемых пикселами, визуальные параметры (яркость, цветность и т.п.) которых могут изменяться. Поэтому формируемые линии, строго говоря, не могут начинаться и заканчиваться  точно в математически определенных точках носителя.

Бесплатная лекция: "2.6 Анализ качества САУ по частотным характеристикам" также доступна.

Ошибка положения формируемых точек определяется уровнем дискретизации или количеством дискретных точек, на которое разбивается носитель. Максимальная погрешность положения точки определяется шагом между двумя соседними пикселами.

По этой же причине даже отображение отрезка прямой линия, строго говоря, не является прямой, как это показано на приведенном ниже рисунке (рис.2-1). Линия представляется набором горизонтальных (или вертикальных) цепочек пикселов, которые  с учетом шага дискретизации наилучшим образом отражают характер генерируемой прямой линии.

В общем случае, если не принимать специальные меры, яркость линии на отдельных участках будет зависеть от  крутизны этих участков.

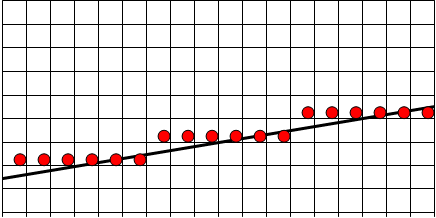Рис.2-1

Удовлетворение требовния минимальных затрат времени на определение координат одной точки формируемой линии обеспечивается за счет использования приближенных методов вычислений, применения целочисленной арифметики, использования специальных алгоритмов, реализуемых программно или на специальных графических процессорах.