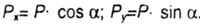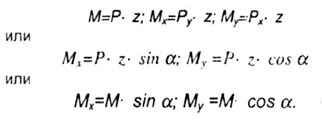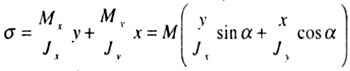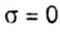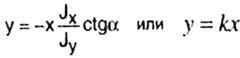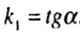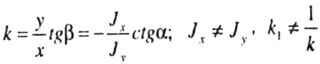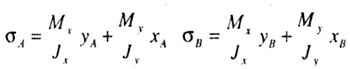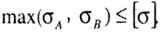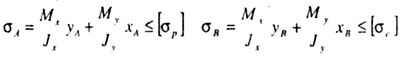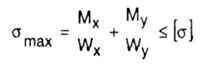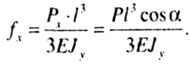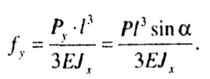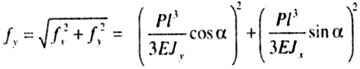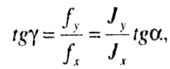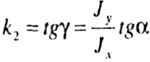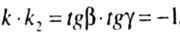Определение напряжений при косом изгибе стержня
Определение напряжений при косом изгибе стержня
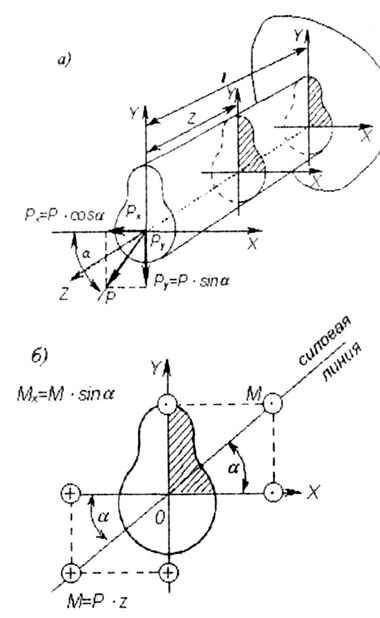
| Косым изгибом называется такой вид изгиба, при котором плоскость нагрузки (силовая линия) изгибающего момента не совпадает ни с одной из главных осей инерции поперечного сечения стержня X, Y (рис. 7.1, а, б). |
| При косом изгибе действующие внешние силы (моменты) представляют их проекциями на главные оси поперечного сечения (рис. 7.1, б), тем самым сводят задачу к случаю поперечного изгиба в двух главных плоскостях. Из рис. 7.1, а, б видно, что: |
|
|
| Изгибающие моменты в расчетном сечении: |
|
|
| При выбранном направлении главных центральных осей инерции положительным октантом будет первый октант (на рис. 7.1, а, б заштрихован). |
|
|
|
|
Рекомендуемые материалы-76% Интерференция в тонких пленках. Определение геометрических параметров поверхностей прозрачных тел интерференционным методом -41% Изучение явлений интерференции и дифракции на примере дифракционной решетки Определить значение силы F, преодолеваемой штоком гидроцилиндра при движении его против нагрузки со скоростью υ = 20 мм/с. Давление на входе в дроссель pН = 20 МПа; давление на сливе pс = 0,3 МПа; коэффициент расхода дросселя μ = 0,62; диаметр отверс При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Hрасп = 9,6 м; длина трубопровода l = 10 м; эквивалентная шероховатость Δ = 0,05 мм; давление в баке p0 = 30 кПа; высота H0 = 4 м; вязкость ж Определение динамической вязкости жидкости по методу Стокса FREE Интерференция в тонких пленках. Определение геометрических параметров поверхностей прозрачных тел интерференционным методом Рис. 7.1 |
| Правило знаков. Изгибающие моменты в расчетном поперечном сечении считаются положительными, если они вызывают в первом (заштрихованном) октанте напряжения растяжения. |
| Нормальные напряжения в точках поперечного сечения с текущими координатами х, у определяются алгебраической суммой напряжений, вызываемых изгибающими моментами Мx и Мy: |
|
|
| где Jx и Jy — моменты инерции поперечного сечения относительно главных, центральных осей инерции сечения X, Y, т. е. изменяются по линейному закону. Уравнение нейтральной (нулевой) линии в сечении найдем, приравняв |
| Ответы совпали. |
|
|
| При х = 0 значение у = 0, т. е. прямая с угловым коэффициентом k проходит через центр тяжести поперечного сечения. |
| При косом изгибе нейтральная линия представляет собой прямую, которая не перпендикулярна к плоскости изгибающего момента , или, что одно и то же, к силовой линии. |
| Силовая линия наклонена к оси X под углом а, следовательно, ее угловой коэффициент равен: |
|
|
| Угловой коэффициент нейтральной линии: |
|
|
| Так как в общем случае Jx не равно Jy, то и k1 не равно — 1/k, следовательно, нулевая длина не перпендикулярна силовой линии, а повернута в сторону главной оси минимального момента инерции. |
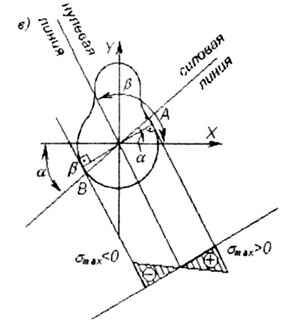
| Нейтральная линия разделяет поперечное сечение на две зоны: |
|
| Максимальные по величине напряжения растяжения возникают в точке А с координатами Xa, Yл, а максимальные напряжения сжатия возникают в точке В с координатами XВ, YВ (рис. 7.1, в): |
|
|
| Получим эпюру нормальных напряжений в расчетном сечении (7.1, в). |
| Условие прочности. Если материал стержня одинаково работает на растяжение и на сжатие, то условие прочности записывается в виде: |
|
|
| Если материал стержня работает на растяжение и на сжатие не одинаково, то расчет проводится раздельно, т. е. проверяются условия прочности: |
|
|
| Для поперечных сечений, имеющих две оси симметрии: |
|
|
| где Wx, Wy — момент сопротивления поперечного сечения относительно главных, центральных осей инерции X, Y. |
| Прогибы при косом изгибе. Прогиб конца консоли от действия Рx направлен по оси X и равен: |
|
|
| Прогиб от действия Рy направлен по оси Y и равен: |
|
|
| Модуль полного прогиба конца консоли |
|
|
| Угол наклона вектора f к оси X |
| Вместе с этой лекцией читают "Список литературы".
|
| т. е. угловой коэффициент |
|
|
| перемножив k на k2 получим: |
|
|
| что свидетельствует о том, что нулевая линия и направление полного прогиба взаимно |