Расчет и анализ чувствительности
Расчет и анализ чувствительности
Основной задачей теории чуствительности является анализ дополнительного движения вызванного вариацией параметров. Такой анализ, в частности, включает количественные оценки, характеризующие влияние одних параметров на другие или на качество технической системы в целом. Обычно анализ дополнительного движения строится на основе нахождения функций чувствительности, получаемых в результате решения дифференциальных уравнений называемых уравнениями чувствительности. Вместе с тем применяются различные косвенные оценки, в том числе частотные или корневые. Будем рассматривать моделирование динамики системы управления в комплексной плоскости. Вектором параметров, по отношению к которому требуется оценить чувствительность системы управления, выберем вектор p. Компонентами вектора могут быть коэффициенты передаточных функций элементов управляющей части системы или объекта управления. В качестве исследуемой характеристики, изменяющейся при вариации p, выберем управляемую переменную y на выходе объекта управления. Тогда чувствительность y к p может быть представлена вектором
|
| (6.5) |
для системы управления, описываемой системой уравнений вида
| Y( p, s) = W( p, s) G(s). | (6.6) |
В лекции "1.3. Многокомпонентные жидкости" также много полезной информации.
В формуле (6.5) v – размерность вектора p,  - начальное (номинальное) значение параметра
- начальное (номинальное) значение параметра  ,
,  - установившееся значение выходного сигнала при
- установившееся значение выходного сигнала при  . Частные производные, входящие в формулу (6.5), вычисляются в точке
. Частные производные, входящие в формулу (6.5), вычисляются в точке  .
.
Рассмотрим вопрос количественной оценки чувствительности установившегося режима к вариации параметров вектора p. Для этого положим s = 0 и G(s) = 1/s. В силу принятых допущений выражение (6.5) значительно упростится без потери существенной информации относительно установившегося режима:
|
| (6.7) |
Расчет чувствительности  включает этапы:
включает этапы:
- задание структуры и состава системы управления, вектора
![]() ;
; - построение W(p,s);
- формирование
![]() ;
; - определение
![]() .
. - вычисление чувствительности по формуле (6.7).
Если анализ диктует необходимость рассмотрения функций чувствительности для установления влияния вектора p на динамику системы управления, то s в формуле (6.7) не должно обнуляться и от полученных функций  следует перейти к временным функциям
следует перейти к временным функциям  на основе известного разложения Хевисайда рациональной алгебраической функции.
на основе известного разложения Хевисайда рациональной алгебраической функции.



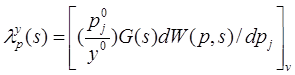
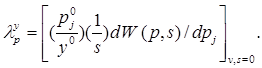
 ;
; .
.



















