Векторные и матричные нормы, сходимость по норме

2.3. Векторные и матричные нормы, сходимость по норме

Наиболее часто используемые нормы векторов

                                         ;

                                                  ;

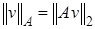
и матриц

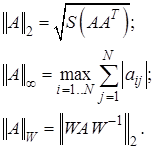
Для любой нормы  справедливы формулы

                                                                                      (2.15)

Рекомендуемые материалы

Если  ‑ симметричная матрица, то . То же относится и к симметризованной матрице .

Рекомендация для Вас - 5 Проекции.

Говорят, что последовательность векторов  сходится по норме  к вектору , если

                                               .

Аналогично, последовательность матриц  сходится к матрице , если

                                               .

Основное свойство, связывающее сходимость со спектром матрицы, выражается утверждением:

                                           (2.16)