Собственные значения и собственные векторы матрицы
2.2. Собственные значения и собственные векторы матрицы
Уравнение (точнее, однородная СЛАУ)  имеет нетривиальное (отличное от нуля) решение тогда и только тогда, когда ее определитель
имеет нетривиальное (отличное от нуля) решение тогда и только тогда, когда ее определитель  .
.
Для некоторого ненулевого вектора  и числового параметра
и числового параметра  можно составить СЛАУ
можно составить СЛАУ
 . (2.7)
. (2.7)
Очевидно, решение (2.7) будет нетривиальным, если
 (2.8)
(2.8)
По определению определителя слева в характеристическом уравнении (2.8) имеем полином степени  от
от  . Значит уравнение (2.8) имеет ровно
. Значит уравнение (2.8) имеет ровно  корней
корней  . Это корни (действительные или комплексные) называются собственными значениями (СЗ) или собственными числами матрицы
. Это корни (действительные или комплексные) называются собственными значениями (СЗ) или собственными числами матрицы  . Используем этот набор собственных чисел, и каждое из них подставим в (2.7). Получим набор из
. Используем этот набор собственных чисел, и каждое из них подставим в (2.7). Получим набор из  систем уравнений. Каждая из них определяет свой вектор
систем уравнений. Каждая из них определяет свой вектор  , соответствующий подставленному в СЛАУ (2.7) собственному значению
, соответствующий подставленному в СЛАУ (2.7) собственному значению  . Полученные векторы называются собственными векторами (СВ) матрицы
. Полученные векторы называются собственными векторами (СВ) матрицы  . Из (2.7) очевидно, что на действие матрицы на собственные векторы сводится к умножению их на собственные числа,
. Из (2.7) очевидно, что на действие матрицы на собственные векторы сводится к умножению их на собственные числа,  .
.
Понятно, что если все СЗ  различны, то различны и соответствующие им СВ, причем они образуют базис в
различны, то различны и соответствующие им СВ, причем они образуют базис в  . Вообще это не всегда так, но например СЗ симметричных матриц различны и действительны, а их СВ образуют базис. Для
. Вообще это не всегда так, но например СЗ симметричных матриц различны и действительны, а их СВ образуют базис. Для  все
все  .
.
Спектральный радиус  матрицы
матрицы  ‑ это наибольшее по модулю собственное число:
‑ это наибольшее по модулю собственное число:
Рекомендуемые материалы
 (2.9)
(2.9)
Для действительных СЗ определяют наименьшее и наибольшее
 . (2.10)
. (2.10)
а также число обусловленности для матрицы  :
:
 (2.11)
(2.11)
Итак, главные спектральные свойства симметричных положительно определенных квадратных матриц, т.е. 
 , с вещественными элементами:
, с вещественными элементами:
1. СЗ  ;
;
2. СВ  образуют ортонормальный базис в
образуют ортонормальный базис в  , т.е.
, т.е.  ;
; 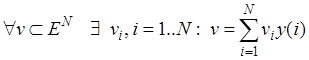
3. 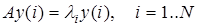
Две матрицы  и
и  называются подобными, если можно указать невырожденную матрицу
называются подобными, если можно указать невырожденную матрицу  , такую, что
, такую, что  . Подобные матрицы
. Подобные матрицы  и
и  имеют одинаковые СЗ. Кроме того, для любой матрицы
имеют одинаковые СЗ. Кроме того, для любой матрицы  с действительными элементами, которая подобна симметричной вещественной матрице
с действительными элементами, которая подобна симметричной вещественной матрице  справедливы свойства 1 и 3. Матрица
справедливы свойства 1 и 3. Матрица  называется матрицей симметризации.
называется матрицей симметризации.
Рекомендуем посмотреть лекцию "Начало раздробленности на Руси".
Отношение Рэлея для произвольного ненулевого вектора  и матрицы
и матрицы  есть дробь
есть дробь  . Если
. Если  , то
, то
 (2.12)
(2.12)
Степень матрицы есть  . Матричный многочлен степени
. Матричный многочлен степени  для матрицы
для матрицы  – это матрица того же размера
– это матрица того же размера
 (2.13)
(2.13)
Его СЗ  получаются из СЗ
получаются из СЗ  матрицы
матрицы  по формуле
по формуле
 (2.14)
(2.14)





















