Сетевые модели

ЛЕКЦИЯ 5

СЕТЕВЫЕ МОДЕЛИ

Основные понятия теории графов. Задача минимизации сети. Алгоритм построения минимального дерева. Задача о кратчайшем пути. Алгоритм Дейкстры. Алгоритм Флойда. Задача о максимальном потоке. Алгоритм расстановки пометок.

Многие задачи линейного программирования можно сформулировать и решить с помощью сетевых моделей. Специальная структура этих задач позволяет разработать эффективные алгоритмы, которые в большинстве случаев основываются на теории линейного программирования. Теоретической основой сетевых моделей является теория графов.

Графы рисуют на бумаге не только те, кто понимают теорию графов, но и люди, которые никогда о ней не слышали. К примеру, любой администратор, изображающий структуру, подчиненных ему подразделений в виде прямоугольников и стрелок между ними, по сути дела, рисует связанный ориентированный граф, хотя он и не знает об этом.

Началом теории графов считается 1736 год, когда вышла в свет статья Эйлера с его знаменитыми рассуждениями о Кенигсбергских мостах. В этой статье Эйлер рассмотрел следующую задачу. В Кенигсберге (ныне г. Калининград) течет река Неман. Она омывает два острова. Между берегами реки и островами во времена проживания в Кенигсберге Эйлера существовали 7 мостов, расположение которых показывает план на Рис. 1.

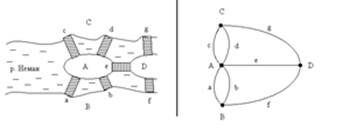
Рис.1.

Рекомендуемые материалы

Задача Эйлера состояла в том, чтобы определить, можно ли выйдя из пункта С (или любого другого пункта) пройти каждый мост только по одному разу и вернуться в исходный пункт. Найденное Эйлером решение задачи о кенигсбергских мостах, а точнее предложенный им при этом метод, был положен в основу теории графов.

Затем около 100 лет эта статья оставалась единственной, а методы теории графов невостребованными практикой. Интерес к графам появился только в середине 19 века благодаря исследованиям электрических сетей, моделей кристаллов и структур молекул. С тех пор сфера применений теории графов непрерывно расширялась и сегодня она представляет собой мощную формальную систему, имеющую необозримое множество областей практического применения.

Основные понятия теории графов

Графом G = (V, X) называется пара двух конечных множеств: множество точек и множество линий, соединяющих некоторые пары точек

Точки называются вершинами (узлами) графа, линии – ребрами графа.

Если задан граф G = (V, X), то V – конечное непустое множество его вершин, X – множество его ребер.

Ребро называется инцидентным по отношению к тем вершинам, которые оно соединяет.

Две вершины графа называются смежными, если существует инцидентное им ребро.

Два ребра называются смежными, если они имеют общую вершину.

Граф называется ориентированный, если он состоит упорядоченных пар вершин. Такой граф называется также направленным графом или орграфом.

В направленном графе ребра изображаются стрелками.

Ребра ориентированного графа имеют определенные фиксированные начало и конец и часто называются дугами.

Дуги орграфа называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления. (соединят одну и туже пару вершин). При этом граф имеет несколько разных дуг, соединяющих одну и туже пару вершин.

Рассмотрим неориентированный граф, состоящий их n вершин. Если от некоторой вершины можно пройти к другой вершине по ребрам графа, то получим маршрут перехода. При этом для одних и тех же вершин может оказаться несколько маршрутов. При решении конкретной задачи в таких случаях приходится выбирать наиболее оптимальный маршрут.

Маршрутом называется последовательность попарно инцидентных вершин V₁, V₂, …, V_i неориентированного графа, т.е. последовательность ребер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего.

Длиной маршрута называется число ребер этого маршрута.

Маршрут принято задавать как последовательность ребер, поскольку это более удобно при наличии кратных ребер.

Маршрут называется замкнутым или циклом, если начальная вершина маршрута совпадает с конечной,

Расстоянием между двумя вершинами называется минимальная длина из всех возможных маршрутов между этими вершинами при условии, что существует хотя бы один такой маршрут.

В маршруте одно и то же ребро может встретиться несколько раз.

Если ребро встретилось только один раз, то маршрут называется цепью.

В орграфе маршрут является ориентированным и называется путем. На путь сразу налагаются важные требования, являющиеся частью определения:

¾ направление каждой дуги должно совпадать с направлением пути;

¾ ни одно ребро пути не должно встречаться дважды.

Поэтому путь — упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны.

В графе цепь, путь и цикл называются простыми, если они проходят через любую из вершин не более одного раза.

Неориентированный граф называется связным, если между любыми двумя его вершинами есть маршрут. В противном случае он называется – несвязным.

Две вершины называются связными, если существует маршрут между ними.

Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).

Сеть — в принципе, то же, что и граф, хотя сетями обычно называют графы, вершины которых определённым образом помечены.

Граф называется взвешенным или сетью, если каждому его ребру поставлено в соответствие некоторое число (вес). Взвешенными графами могут быть схемы в электронике, электрические схемы, карты автомобильных и железных дорог и др. Например, на картах автодорог вершины являются населенными пунктами, ребра – дорогами, а весом – числа, равные расстоянию между населен­ными пунктами.

В строительстве сетевые графы применяются для наглядного изображения некоторого комплекса работ или производственных процессов. Ребрам графа могут соответствовать числа, означаю­щие длину, уклон, запланированное время и другие характерис­тики.

Задача минимизации сети

Задача минимизации сети состоит в нахождении ребер, соединяющих все узлы сети и имеющих минимальную суммарную длину. Для решения задачи необходимо построить минимальное дерево-остов, применяя следующий итеративный процесс. Начать с любого узла и соединить его с ближайшим узлом сети. Соединенные узлы образуют теперь связное множество, а остальные узлы – несвязное. Далее в несвязном множестве выбрать узел, расположенный ближе всего к одному из узлов связного множества. Скорректировать соответствующим образом связное и несвязное множества, а дугу, по которой произошло присоединение запомнить. Процесс повторять до тех пор, пока все узлы не окажутся в связном множестве. Выбранные дуги образуют минимальное дерево-остов. Его длина равна сумме длин этих дуг.

Задача о кратчайшем пути

Задача о кратчайшем пути состоит в нахождении связанных между собой дорог на транспортной сети, которые имеют минимальную длину от исходного пункта до пункта назначения. Решение задач данного типа находится с помощью применения следующего алгоритма. Каждому узлу сети будем приписывать временные пометки равные расстоянию от начального узла до данного узла. Если оказывается, что узел принадлежит кратчайшему маршруту, то временную пометку объявляем постоянной. На первой итерации начальному узлу приписывается постоянная пометка равная нулю, а остальным узлам – временные пометки, равные длине дуги из начального узла в рассматриваемый узел, если такая дуга существует. Затем, до тех пор пока конечный узел не получит постоянную пометку выполняются следующие две процедуры: 1) среди временных пометок выбирается минимальная и объявляется постоянной; 2) для всех временно помеченных узлов вычисляются новые временные пометки, меньшей из двух величин – старой временной пометки рассматриваемого узла и суммы постоянной пометки последнего постоянно помеченного узла и длины дуги, соединяющей последний постоянно помеченный узел с рассматриваемым узлом. Если при этом постоянную пометку получает конечный узел, то кратчайший маршрут найден. Дуги, входящие в этот маршрут определяются следующим образом: если разность между постоянными пометками начального и конечного узлов данной дуги равна длине дуги, то эта дуга принадлежит кратчайшему маршрут.

Задача о кратчайшем пути является частным случаем транспортной задачи в сетевой постановке (или, что то же самое, задачи об оптимальном потоке). Для этого достаточно присвоить вершине s единичный запас, вершине t единичную потребность, все остальные вершины положить нейтральными, а дугам присвоить неограниченные пропускные способности. Однако, как правило, более рациональным оказывается использование конкретных свойств данной задачи и решение ее специальными (частными) методами.

Задача о максимальном потоке

Задачу о максимальном потоке в сети можно сформулировать как задачу линейного программирования и решить ее обычным симплексным методом. Однако благодаря специальной структуре этой задачи ее решение может быть получено с помощью более эффективного алгоритма.

Рассмотрим сеть, в которой с каждой дугой сопоставлено положительное число b_ij называемое пропускной способностью дуги. В сети выделяют два специальных узла. Один из них называется источником и обозначается s; другой называется стоком и обозначается t. Сеть можно рассматривать как водопроводную систему, в которой трубы соответствуют дугам, источник воды соответствует источнику s, сток воды - стоку t, а соединения между трубами - остальным узлам сети. Пропускная способность дуги здесь соответствует поперечному сечению трубы. Надо найти, какой максимальный поток воды можно пропустить из источника в сток в этой водопроводной системе.

Чтобы сформулировать эту задачу более точно, введем сначала понятие потока в сети. Потоком из источника s в сток t в сети называется множество неотрицательных чисел х_ij (каждое из которых поставлено в соответствие некоторой дуге сети), если эти числа удовлетворяют следующим линейным ограничениям:

                               (1)

                                     v ³  0,

                        0 £ x_ij £ b_ij для всех i, j               (2)

Здесь первая сумма берется по дугам, ведущим в узел j, а вторая сумма – по дугам, ведущим из узла j.

Неотрицательное число v, фигурирующее в (1), называется величиной потока. Число x_ij называется потоком по дуге (i, j), или дуговым потоком.

Заметим, что ограничения (1) выражают тот факт, что в каждый узел (кроме источника и стока) приходит столько потока, сколько из него выходит (условие сохранения). Ограничение (2) означает, что поток x_ij по дуге ограничен пропускной способностью дуги b_ij.

В том случае, когда сеть является цепью с источником s и стоком t, максимальная величина потока, который может быть пропущен через сеть, ограничивается минимальной из пропускных способностей дуг этой цепи. Здесь дуга с минимальной пропускной способностью является «узким местом» в сети. Теперь мы дадим общее определение «узкого места» в произвольной сети, для чего введем понятие разреза.

Разрез - это множество дуг, исключение которых из сети отделит некоторое множество узлов от остальной части узлов.

На рис.2 изображена сеть, в которой разрез, состоящий из дуг (2, 4) и (3, 4), отделяет узел 4 от группы узлов 1, 2, 3.

Пропускная способность разреза - это сумма пропускных способностей всех дуг разреза.

Пропускная способность разреза, показанного на рис.2 равна b₂₄ + b₃₄.

Разрез, разделяющий s и t, является аналогом «узкого места» в произвольной сети. Ясно, что благодаря ограничениям (1) – (2) величина v максимального потока меньше или равна пропускной способности любого разреза, разделяющего s и t. Величина максимального потока всегда равна минимальной пропускной способности всех разрезов, разделяющих s и t.

Минимальный разрез - это разрез, разделяющий источник s и сток t и обладающий минимальной пропускной способностью.

Задача о максимальном потоке часто встречается на практике, причем число узлов и дуг в сети нередко достигает нескольких тысяч. Поэтому для решения таких задач необходимо использовать эффективную процедуру вычислений. Благодаря простоте постановки задачи о максимальном потоке был разработан эффективный рекуррентный алгоритм поиска оптимального решения (максимального потока), использующий процедуру расстановки пометок. Перейдем к описанию этого алгоритма.

Алгоритм состоит из двух шагов.

Шаг 1 – это процесс, в ходе которого узлы получают пометки.

Шаг 2 - это изменение потока.

Шаги 1 и 2 повторяются до тех пор, пока увеличение потока становится невозможным.

Шаг 1 (процесс расстановки пометок). На шаге 1 каждый узел находится в одном из трех состояний: «помечен и просмотрен», «помечен и не просмотрен» или «не помечен». Вначале все узлы не помечены. Как уже было сказано ранее, пометка произвольного узла j всегда состоит из двух частей. Первая часть – число, указывающее максимальную величину потока, который можно «послать» из источника s в j, не нарушая ограничений на пропускные способности дуг. Вторая часть пометки – номер узла i, который указывает, что можно «послать» поток из i в j.

Прежде всего источник s получает пометку [µ, -],которая указывает, что из данного узла может вытекать поток бесконечно большой величины Теперь узел s «помечен и не просмотрен», а все остальные узлы «не помечены».

Вообще выберем любой помеченный и непросмотренный узел j. Пусть он имеет пометку [+q_j, i] или [-q_j, i]. Два узла будем называть соседними, если они соединены дугой. Из всех узлов, соседних с j, выделим те узлы k, которые не помечены и для которых x_jk < b_jk (обратите внимание на индексы jk, такая последовательность означает, что поток направлен от узла j к узлу k). Припишем каждому узлу k пометку [+q_k, j], где q_k = min [q_j, b_jk – x_jk] Теперь такие узлы k «помечены и не просмотрены». После этого всем соседним с j узлам k, которые не помечены и для которых х_kj > 0, приписываем пометку [-q_k, j], где q_k = min [q_j, x_kj]. Теперь такие узлы k также «помечены и не просмотрены». После этого все узлы, соседние с j имеют пометки. Узел j считается помеченным и просмотренным, и его можно больше не рассматривать на этом шаге. Может оказаться, что некоторые соседние с j узлы помечены, а остальные не могут быть помечены (либо все соседние с j узлы не могут быть помечены); в этих случаях узел j также считается помеченным и просмотренным. Знаки «+» и «-» в первой части пометок указывают, как должен быть изменен поток на шаге 2.

2.0 Раздробленность на Руси - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Продолжим приписывать пометки узлам, которые являются соседними для помеченных и непросмотренных узлов, до тех пор, пока либо узел t окажется помеченным, либо нельзя будет больше пометить ни один узел и сток t окажется непомеченным. Если t не может быть помечен, то не существует пути из s в t, увеличивающего поток, и, следовательно, построенный поток максимален. Если же t помечен, то на шаге 2 можно найти путь, увеличивающий поток.

Шаг 2 (изменение потока). Предположим, что сток t имеет пометку [+q_t, k]. Тогда заменим х_kt на х_kt + q_t. Если же он имеет пометку [-q_t, k], то х_tk заменим на x_tk - q_t. Затем в любом из этих случаев переходим к узлу k. Вообще если узел k имеет пометку [+q_j, k], то х_jk заменим на х_jk + q_t и перейдем к узлу j, если узел k имеет пометку [-q_j, k], заменим на х_kj на x_kj - q_t. и перейдем к j. Продолжим эти действия, пока не достигнем источника s. После этого сотрем все старые пометки узлов и вновь перейдем к шагу 1.

Когда алгоритм заканчивается на шаге 1, то получается множество  помеченных узлов и множество дуг, одна вершина у которых помечена, а другая нет. Множество таких дуг образуют минимальный разрез, поток через который равен его пропускной способности. Таким образом, получен максимальный поток. С другой стороны, каждый раз величина потока увеличивается по крайней мере на единицу (предполагаем, что пропускные способности дуг и исходный поток являются целочисленными). Поскольку величина максимального потока ограничена сверху пропускной способностью минимального разреза (целым числом), то алгоритм расстановки пометок конечен.

Отсюда следует, что возможны два следующих случая:

1. Стоку t приписана пометка [+q_t, k]. В этом случае увеличивающий путь потока найден и поток по каждой дуге этого пути может быть увеличен на величину q_t. После изменения дуговых потоков текущие пометки стираются и вся описанная выше процедура выполняется заново.

2. Сток t не может быть помечен. Это означает, что увеличивающий путь потока не может быть найден. Следовательно, построенные дуговые потоки образуют максимальный поток (оптимальное решение).