Целочисленное программирование
ЛЕКЦИЯ 4
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ
Область применения целочисленного программирования. Классификация задач целочисленного программирования. Математическая модель задачи целочисленного программирования. Методы решения задач целочисленного программирования
Целочисленное программирование (ЦП) — раздел линейного программирования, включающий дополнительное требование, состоящее в том, что значения переменных должны быть целыми неотрицательными числами.
Важность целочисленного программирования для задач экономики и управления, заключается в том, что многие, ресурсы неделимы и участвуют в процессе только целыми единицами. Грузовики, самолеты, поезда, распределение рабочих по станкам и т.п. — все эти объекты или процессы поступают или осуществляются только в целых единицах.
В терминах ЦП формулируется широкий круг прикладных задач оптимизации, связанных с неделимостью, фиксированными доплатами, условиями логического типа, с наличием стандартов при проектировании, комбинаторные задачи.
Классификация прикладных задач
Выделяют следующие основные источники целочисленности:
Рекомендуемые материалы
1. Задачи с неделимостями. В таких задачах физическая неделимость единицы xj есть требование постановки, т.е. физическая сущность xj такова, что xj могут принимать только целочисленные значения. Это требование возникает в случаях, когда:
¾ используемыми переменными являются крупные объекты (количество самолетов, турбин, заводов и т.д.);
¾ интерпретация результатов решения задачи такова, что требования целочисленности подразумевается априори. К таким постановкам относятся задачи, использующие в качестве интенсивности производства или распределения некоторые стандартные единицы – модули, комплексы машин и т.д.
Применение:
¾ задачи оптимизации средств в доставке грузов;
¾ задачи минимизации числа транспортных единиц для осуществления заданного графика перевозок;
¾ задачи минимизации порожнего пробега автомобилей при реализации заданного графика;
¾ задачи оптимизации и комплектования стандартными модулями некоторого производства;
2. Задачи размещения. Постановка задачи предполагает выбор вариантов плановых решений из набора возможных таким образом, чтобы совокупность вариантов оптимизировала суммарный показатель качества. Тогда формализация множества вариантов плановых решений для некоторого производственного объекта возможно только во множестве Z.
Применение:
¾ задача планирования, развития и размещения производства;
¾ задача специализации;
¾ задача кооперирования.
3. Комбинаторные задачи. Данный тип прикладных задач делится на 2 класса:
¾ задачи, укладывающиеся в схему классической задачи о коммивояжере;
¾ задачи теории расписаний.
Формальная схема постановки: найти путь минимальной длины проходящий раз и только раз через каждую вершину графа, непрерывный и заканчивающийся в исходной вершине. Применение: задачи нахождения маршрутов развозки груза, минимизирующие пробег. Формальная постановка задачи теории расписаний: упорядочить во времени использование системы машин для обработки некоторого множества изделий. Применение: большинство задач организации производственного процесса.
4. Задачи о покрытии. Формальная схема постановки задачи о покрытии: найти минимальное подмножество множества ребер данного графа, содержащего все вершины графа. Формальная схема постановки задачи о максимальном потоке в сети: определить разрез с минимальной пропускной способностью, т.е. максимизировать поток через данную сеть.
Применение:
¾ задача синтеза логических сетей;
¾ задачи синтеза оптимальных по стоимости, компактности, надежности и т.д. систем переработки информации (управляющих систем).
¾ задачи поиска максимального потока;
Методы решения задач целочисленного программирования
Методы решения задач целочисленного программирования можно классифицировать как методы отсечений и комбинаторные методы. Исходной задачей для методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требования целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется до тех пор, пока координаты допустимого решения не станут целочисленными. Название «методы отсечений» связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами.
В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений, разумеется, на первый план здесь выдвигается проблема разработки тестовых процедур, позволяющих непосредственно рассматривать лишь относительно небольшую часть указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом. Наиболее известным комбинаторным методом является метод ветвей и границ, который также опирается на процедуру решения задач с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального «разбиения» пространства допустимых решений и отбрасывания областей, не содержащих допустимых целочисленных решений.
В случае, когда целочисленные переменные являются булевыми, применяются комбинированные методы. Булевы свойства переменных существенно упрощают поиск решения. Алгоритм метода отсечений для решения полностью целочисленной задачи. Необходимым условием применения данного алгоритма является целочисленность всех коэффициентов и правых частей ограничений исходной задачи. Любое ограничение с рациональными коэффициентами легко приводится к требуемому виду путем умножения ограничения на наименьший общий знаменатель входящих в него коэффициентов. Алгоритм состоит в следующем. На первом шаге решается задача с ослабленными ограничениями, не содержащая условий целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае следует ввести дополнительные ограничения, порождающие (вместе с некоторыми ограничениями) новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи.
Методы решения задач целочисленного линейного программирования основаны на использовании вычислительных возможностей методов линейного программирования. Обычно алгоритмы целочисленного программирования включают три шага.
Шаг 1. "Ослабление" области допустимых решений задачи целочисленного линейного программирования путем замены любой двоичной переменной у непрерывным ограничением 0 <у < 1 и отбрасывания требования целочисленности для всех остальных переменных. В результате получается обычная задача линейного программирования.
Шаг 2. Решение задачи линейного программирования без учета целочисленности.
Шаг 3. В полученное оптимальное решение, добавляются специальные ограничения, которые итерационным путем изменяют область допустимых решений задачи таким образом, чтобы, в конечном счете, получилось оптимальное решение, удовлетворяющее требованиям целочисленности.
Разработаны два общих метода генерирования специальных ограничений для шага 3.
1. Метод отсекающих плоскостей.
2. Метод ветвей и границ.
Метод отсекающих плоскостей
Сущность метода отсекающих плоскостей состоит в том, что сначала задача решается без условия целочисленности. Если полученный план будет целочисленным, то задача решена, в противном случае к ограничению задачи добавится новое ограничение, обладающее следующими свойствами:
1. оно должно быть линейным,
2. должно отсекать найденный нецелочисленный план,
3. не должно отсекать ни одного целочисленного плана.
Дополнительные ограничения, обладающие указанными свойствами, называются правильным отсечением. Затем полученные оптимизационные задачи решают с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д. Геометрически добавление каждого линейного ограничения отвечает проведению плоскости (гиперплоскости), которая отсекает от многоугольника (многогранника) некоторую его часть вместе с оптимальной точкой с нецелочисленной координацией, но не затрагивает ни одной из целочисленных точек этого многоугольника.
Данный метод впервые был предложен Р.Е. Гомори в 1957-1958гг. Основная идея метода состоит в том, что на каждом шаге рассматривается задача с ослабленными ограничениями без требования целочисленности, для которой по специальному алгоритму строится некоторое дополнительное линейное ограничение (отсечение), отсекающее только некоторые нецелочисленные точки. Он существенно использует известную симплексную процедуру. Отправной точкой для решения задачи является решение ее непрерывного аналога, т.е. задачи линейного программирования без учета целочисленности. Если получаемый в результате оптимальный план содержит только целые компоненты, то автоматически получается задача целочисленного линейного программирования. В противном случае в системе ограничений задачи должно быть добавлено такое ограничение, для которого:
1. найденный нецелочисленный оптимальный план не удовлетворяет вновь добавляемому ограничению,
2. любой допустимый целочисленный план задачи удовлетворяет вновь добавляемому ограничению.
Метод ветвей и границ
Согласно общей идее метода, сначала решается задача с ослабленными ограничениями (задача линейного программирования). Пусть xr – целочисленная переменная, значение которой в оптимальном решении ослабленной задачи является дробным. Интервал
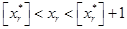
не содержит допустимых целочисленных компонент решения. Поэтому
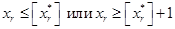
Введение этих условий в задачу с порождает две не связанные между собой задачи. Учет в процессе ветвления необходимых условий целочисленности позволяет исключить части области допустимых решений, не содержащие точек с целыми координатами.
Затем каждая подзадача решается как задача линейного программирования (с целевой функцией исходной задачи). Если полученный оптимум оказывается допустимым для целочисленной задачи, такое решение следует зафиксировать как наилучшее. В противном случае подзадача в свою очередь должна быть разбита на две подзадачи опять при учете условия целочисленности переменных, значения которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается лучше имеющегося, оно фиксируется вместо зафиксированного ранее. Процесс ветвления продолжается до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена невозможность улучшения имеющегося решения. В этом случае зафиксированное допустимое решение является оптимальным.
Эффективность вычислительной схемы метода можно повысить, введя в рассмотрение понятие границы, на основе которого делается вывод о необходимости дальнейшего разбиения каждой из подзадач. Если оптимальное решение подзадачи с ослабленными ограничениями обеспечивает худшее значение целевой функции, чем имеющееся решение, эту подзадачу далее рассматривать не следует. В таких случаях говорят, что подзадача прозондирована, и ее можно вычеркнуть из списка подзадач, порожденных исходной задачей. Иными словами, как только получено допустимое целочисленное решение некоторой подзадачи, соответствующее значение целевой функции может быть использовано в качестве границы, которая позволяет формализовать процедуру исключения прозондированных подзадач.
Применение метода ветвей и границ рассмотрим на примере.
Пример. Методом ветвей и границ найти максимальное значение функции F(x) = 2x1 + 3x2 при ограничениях
3x1+4x2 ≤ 24
2x1+5x2 ≤ 22
x1,2≥0 - целые
1-й шаг метода ветвей и границ. Решается задача линейного программирования с отброшенными условиями целочисленности с помощью симплекс-метода (табл. 1 – 3).
По данным табл. 3 запишем оптимальное нецелое решение
| x*1=2 | 4 | ; x*2=2 | 4 | ; Fmax=16 | 6 |
| 7 | 7 | 7 |
Таблица 1 - симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |
| x1 | x2 | ||
| x3 | 24 | 3 | 4 |
| x4 | 22 | 2 | 5 |
| F | 0 | -2 | -3 |
Таблица 2 - симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |
| x1 | x4 | ||
| x3 | 32/5 | 7/5 | -4/5 |
| x2 | 22/5 | 2/5 | 1/5 |
| F | 66/5 | -4/5 | 3/5 |
Таблица 3 - симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |
| x3 | x4 | ||
| x1 | 32/7 | 5/7 | -4/7 |
| x2 | 18/7 | -2/5 | 3/7 |
| F | 118/7 | 4/7 | 1/7 |
Графическая интерпретация задачи приведена на рис. 1. Здесь ОДЗП представлена четырехугольником ABCD, а координаты вершины С совпадают с x*1 и x*2 . Обе переменные в оптимальном решении являются нецелыми, поэтому любая из них может быть выбрана в качестве переменной, инициирующей процесс ветвления.
Пусть это будет x2. Выбор x2 порождает две подзадачи (2 и 3), одна из них получается путем добавления ограничения x2≥3 к исходной задаче, а другая – путем добавления ограничения x2≤2. При этом ОДЗП разбивается на две заштрихованные области (рис. 1), а полоса значений 2 < x2 < 3 исключается из рассмотрения. Однако множество допустимых целочисленных решений сохраняется, порожденные подзадачи содержат все целочисленные решения исходной задачи.

Рис. 1. Графическая интерпретация решения примера методом ветвей и границ
2-й шаг метода ветвей и границ. Осуществляется выбор одной из обозначенных ранее подзадач. Не существует точных методов определения, какой из подзадач отдать предпочтение. Случайный выбор приводит к разным последовательностям подзадач и, следовательно, к различным количествам итераций, обеспечивающих получение оптимального решения.
Пусть вначале решается подзадача 3 с дополнительным ограничением x2≤2 или x2 + x5 = 2 . Из табл. 3 для переменной x2 справедливо следующее выражение -2/7x3+3/7x4+x2=18/7 или x2=18/7+2/7x3-3/7x4, тогда 2/7x3-3/7x4+x5=-4/7 . Включаем ограничение в табл. 3, при этом получим новую таблицу (табл. 4).
Осуществляя оптимизацию решения, переходим к табл. 5, которой соответствует решение
| x*1=5 | 1 | ; x*2=2 | ; Fmax=16 | 2 |
| 3 | 3 |
Переменная x1 нецелая, поэтому ветвление необходимо продолжить; при этом возникают подзадачи 4 и 5 с ограничениями x1≤5 и x1 ≥6 соответственно. Полоса значений 5 < x1 < 6 исключается из рассмотрения.
Таблица 4 - симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |
| x3 | x4 | ||
| x1 | 32/7 | 5/7 | -4/7 |
| x2 | 18/7 | -2/5 | 3/7 |
| x5 | -4/7 | 2/7 | -3/7 |
| F | 118/7 | 4/7 | 1/7 |
Таблица 5 - симплекс-таблица для задачи ЛП
| базисные переменные | Свободные члены | Небазисные переменные | |
| x3 | x5 | ||
| x1 | 16/3 | 1/3 | -4/3 |
| x2 | 2 | 0 | 1 |
| x4 | 4/3 | -2/3 | -7/3 |
| F | 50/3 | 2/3 | Вам также может быть полезна лекция "Управление производством". 1/3 |
3-й шаг метода ветвей и границ. Решаются подзадачи 4 и 5. Из рис. 1 видно, что оптимальное целочисленное решение подзадачи 4 достигается в вершине К с координатами x*1=5, x*2=2, однако это не означает, что найден оптимум исходной задачи. Причиной такого вывода являются еще не решенные подзадачи 3 и 5, которые также могут дать целочисленные решения. Найденное целочисленное решение F = 16 определяет нижнюю границу значений целевой функции, т.е. меньше этого значения оно быть не должно.
Подзадача 5 предполагает введение дополнительного ограничения x1≥6 в подзадачу 3 . Графическое решение на рис. 1 определяет вершину L с координатами x*1=6, x*2=3/2 , в которой достигается оптимальное решение подзадачи 5: Fmax = 16.5 . Дальнейшее ветвление в этом направлении осуществлять нецелесообразно, так как большего, чем 16, целого значения функции цели получить невозможно. Ветвление подзадачи 5 в лучшем случае приведёт к другому целочисленному решению, в котором F = 16.
4-й шаг метода ветвей и границ. Исследуется подзадача 2 с ограничением x2≥3, находится её оптимальное решение, которое соответствует вершине М (рис. 1) с координатами x*1=3.5, x*2=3. Значение функции цели при этом Fmax =16, которое не превышает найденного ранее решения. Таким образом, поиск вдоль ветви x2≥3 следует прекратить.
Отметим, что алгоритм метода ветвей и границ является наиболее надёжным средством решения целочисленных задач, он положен в основу большинства прикладных программ для ПЭВМ, используемых для этих целей.





















