Конечно-разностные методы

Конечно-разностные методы

Задача: Дано:

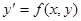
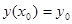
Пусть отрезок  разбит на n частей одинаковой длины h,

               — узлы.

 Найти:  — значения y(x) в узлах.          

Явные конечно-разностные методы используют соотношения вида

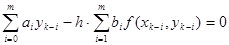
Рекомендуемые материалы

где коэффициенты  ,  подбираются так, чтобы формула была точна для многочленов наивысшей степени.

Неявные конечно-разностные методы используют соотношения вида

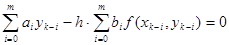
где новое значение y_k присутствует в обеих суммах.

Простейшие методы такого типа получаются на основе квадратурных формул интегрирования:

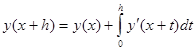
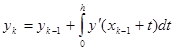
По формуле трапеций получаем

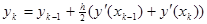
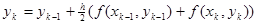
— неявный конечно-разностный метод.

Для использования формулы Симпсона применяют другое равенство

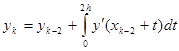
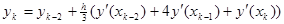
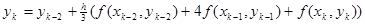
Если Вам понравилась эта лекция, то понравится и эта - Органы управления корпорацией.

— неявный конечно-разностный метод.

Формулу прямоугольников применим также для равенства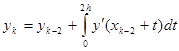

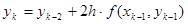
—явный конечно-разностный метод.

Замечание: вторая и третья формулы имеют низкую сходимость, т.е. при уменьшении h погрешность уменьшается медленнее, чем в первой формуле.