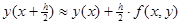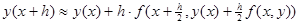Метод Эйлера. Методы Рунге-Кутта

Метод Эйлера. Методы Рунге-Кутта

Пусть отрезок  разбит на n частей,

 — точки деления (узлы), .

При m = 1, формула из § 1 имеет вид:

 — формула Эйлера.

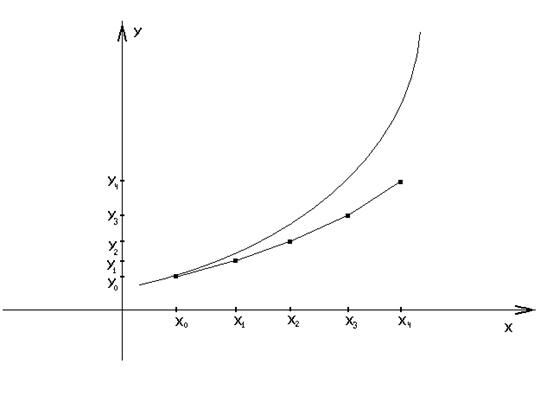
Методы Рунге-Кутта — класс методов, включающий в себя метод Эйлера.

Общая идея методов:

Пусть даны параметры:

Рекомендуемые материалы

q, a₂,…,a_q; p₁,…,p_q; b_ij, 0 < j < i £ q.

Найдем последовательно:

– – – – – – – – – – – – –

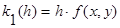
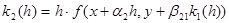
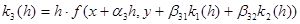
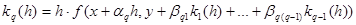
Тогда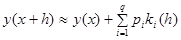

Т.е.  находят последовательно по рекуррентной формуле

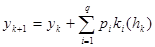
Частные случаи:

1) q = 1, p₁ = 1 — метод Эйлера.

2) q = 2, p₁ =  = p₂; a₂ = 1 = b₂₁

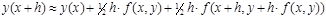
Обоснование справедливости формулы:

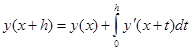
Заменим интеграл квадратурной формулой трапеций

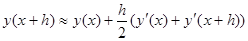
т.к.  получаем

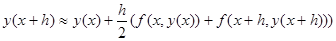
Заменим в правой части по формуле Эйлера

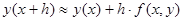
Тогда

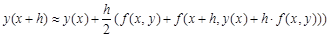
3) q = 2, p₁ = 0, p₂ = 1; a₂ =  = b₂₁

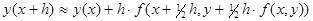
Обоснование справедливости формулы:

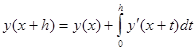
Лекция "7.1 Факторы, влияющие на формирование цветовой среды" также может быть Вам полезна.

Заменим интеграл квадратурной формулой прямоугольников

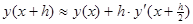
Заменим в правой части по формуле Эйлера