Простейшие квадратурные формулы. Составные формулы

Простейшие квадратурные формулы. Составные формулы

Задача: вычислить  для f(x), непрерывной на [a,b].

Опр. Квадратурная формула — , определяемая узлами

x₀, x₁, ...,  x_n  и весами q₀, ...,  q_n .

Квадратурная формула называется точной для многочленов степени m, если для любого многочлена, степени ≤ m, подставленной вместо f(x), формула дает точное равенство.

I. Формула прямоугольников.

.

Формула точна для многочленов степени 1.

Рекомендуемые материалы

II. Формула трапеций.

, где .

Формула также точна для многочленов степени 1.

III. Формула Симпсона.

Пусть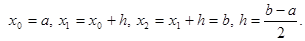

.

Формула также точна для многочленов степени 2 (без док-ва).

Составные формулы получаются, если [a,b] разбить на N частей, на каждой части применить простую формулу, и результаты сложить.

Пусть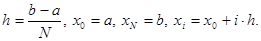

Составная формула прямоугольников:

.

Ещё посмотрите лекцию "9 Межличностные конфликты" по этой теме.

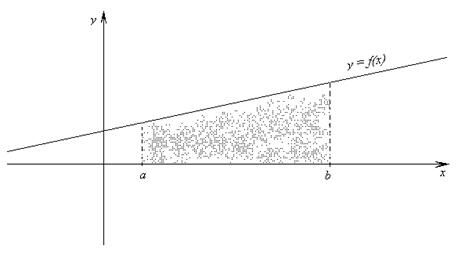
Составная формула трапеций:

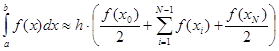
Пусть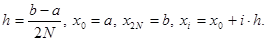

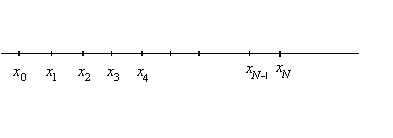
Составная формула Симпсона:

.