МПШ с конечным или счетным числом состояний
§5. МПШ с конечным или счетным числом состояний.
5.1. Пусть 
– конечное или счетное множество, причем будем использовать обозначения
. Пусть 
- МПШ со значениями в и семейством переходных вероятностей
. Положим
Очевидно, что 
Следовательно:
а) 
для любых 
;
б) 
для любых 
;
в) 
для любых .
Пусть
– ограниченная функция. Тогда функция
, определенная по формуле
(17)
Рекомендуемые материалы
является равномерно ограниченной.
Пусть 
и 
, а 
определена формулой:
(18)
Заметим, что соотношение Чепмена-Колмогорова в данном случае будет иметь вид:
(19)
Обозначим через 
- мощность множества. Нам понадобятся также следующие обозначения:
i) 
- матрица размера 
с элементами
;
ii) 
-мерный вектор (-столбец), компонентами которого являются
;
iii) 
-мерный вектор с компонентами 
;
iv) 
- транспонированная матрица ;
v) 
- мерный вектор-строка с компонентами .
Тогда (17) – (19) можно переписать в виде:
, 
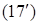
5.2. Займемся теперь выводом обратного и прямого уравнений Колмогорова соответствующих МПШ с конечным или счетным числом состояний.
5.2.1. Пусть 
- множество такое, что для любой последовательности 
из существуют пределы:
1)
для 
;
2) 
где
– символ Кронекера.
Если, для каждой пары
, существует конечный предел
(20)
то ясно, что содержит такие последовательности , для которых 
и
(21)
Заметим, что если существует предел (20), то имеем:
1) если
, то для любых 
справедливо неравенство 
(так как
);
2) если 
, то для любых 
следует, что
, вытекающее из того факта, что 
, где
;
3) 
для любых
, вытекающее из неравенства:
где
. Таким образом, мы приходим к следующему утверждению:
Теорема 2. Пусть для любых 
существует предел: 
и 
Тогда дифференцируема по 
и удовлетворяет обратным уравнениям Колмогорова:
(22)
Доказательство. В силу условий теоремы и соотношения Чепмена-Колмогорова, имеем
Отсюда следует, что:
Доказательство закончено.
5.2.2. Аналогичным образом можно вывести прямые уравнения Колмогорова.
Пусть 
Из (19) следует, что при 
справедливо равенство
. (23)
Переходя к пределу когда 
и 
в (23), имеем
(23a)
Из (23a), в частности, следует, что для 
удовлетворяет прямому уравнению Колмогорова
(24)
5.2.3. Замечания. 1) В §14 главы 3 мы уже вывели прямое уравнение Колмогорова (23) при более слабых предположениях, опираясь на теорию точечных случайных процессов.
2) В §15 главы 3 нами были получены условия разрешимости уравнения Колмогорова (23).
5.3. Приведем без доказательства один результат, касающийся однородных МПШ с конечным или счетным числом состояний.
Теорема 3. Пусть – однородный МПШ с конечным или счетным числом состояний. Тогда существуют конечные или бесконечные пределы
Обратите внимание на лекцию "3.2 Методика решения задачи параметрической оптимизации".
причем, 1) если, то 
– конечно; 2) 
либо конечно, либо
;
3) 
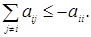
Замечание. Для однородных МПШ с конечным или счетным числом состояний с помощью матрицы 
размера можно произвести следующую классификацию состояний:
1) состояние i называется мгновенным, если , в противном случае (т.е. 
), его называют задерживающим;
2) состояние i называют регулярным, если 
(нерегулярным, если 
), причем, если все состояния регулярны, то однородный МПШ называется консервативным.
