Уравнения Колмогорова МПШ

§4. Уравнения Колмогорова  МПШ.

4.1. Выше приведенная классификация МПШ основана на идее линеаризации соотношения Чепмена–Колмогорова, состоящей в том, что на вероятности перехода накладываются условия, которые позволяют перейти от (нелинейного) соотношения Чепмена-Колмогорова для вероятностей перехода к линейным интегро-дифференциальным уравнениям относительно этих переходных вероятностей. В данном параграфе мы приведем общие соображения о способе получения этих уравнений.

4.2. Пусть - класс функций, таких, что для и существуют пределы:

                                                          (11)

                                                                           (12)

Очевидно, что для  - линейный оператор, а - линейное подпространство . Положим Пусть

 ,тогда для левой производной по функции  справедливы равенства:

        (13)

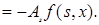
Рекомендуемые материалы

Поэтому из (12) и (13) следует, что

                                                   (14)

Если , где  то  и  удовлетворяет уравнению

                                                        (15)

Уравнения (14) и (15) называются обычно обратными уравнениями Колмогорова.

4.3. Аналогичные рассуждения применимы и к семейству .

         Пусть - множество мер на  и,  а -  подмножество мер, таких, что существуют пределы для любого и:

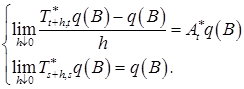
Положим Если такое, что, тогда существует . Отсюда следует, что

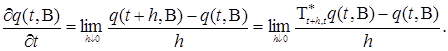
Обратите внимание на лекцию "1.9 Звуковые платы".

Стало быть, и удовлетворяет уравнению:

                                                                         (16)

Уравнение (16) называется прямым уравнением Колмогорова.

Дальнейшие исследования связаны с решением следующих проблем:

i) какова структура операторов и  ,

ii) ii) при выполнении каких условий уравнения Колмогорова  имеют единственное решение.