Переходные вероятности. Определение марковского процесса
§1. Переходные вероятности. Определение марковского процесса.
1.1. Пусть имеется стохастический базис  . Пусть на стохастическом базисе задан случайный процесс
. Пусть на стохастическом базисе задан случайный процесс  со значениями в
со значениями в  , где
, где  – польское пространство. Будем считать, что
– польское пространство. Будем считать, что 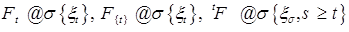
Определение. Случайный процесс  называется марковским, если для
называется марковским, если для  , Р – п.н.
, Р – п.н.
 (1)
(1)
для любого  .
.
Замечание. В силу теоремы Бореля для каждого  существуют:
существуют:
а) измеримый функционал , обозначаемый через
, обозначаемый через  , такой, что
, такой, что  , следовательно
, следовательно 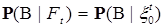
Р – п.н.
б) измеримая функция , обозначаемая через
, обозначаемая через  , такая, что
, такая, что  , следовательно
, следовательно  Р – п.н.
Р – п.н.
Рекомендуемые материалы
причем, в силу (1) Р – п.н.  , т.е.
, т.е.  Р – п.н.
Р – п.н.
1.2. Пусть – измеримое пространство, Е – польское (полное сепарабельное метрическое) пространство,
– измеримое пространство, Е – польское (полное сепарабельное метрическое) пространство,  .
.
Определение. Пусть , обозначаемая
, обозначаемая , такая, что
, такая, что  и
и
1)  - при фиксированных
- при фиксированных  – мера;
– мера;
2)  - при фиксированных
- при фиксированных  – измеримая (по Борелю) функция.
– измеримая (по Борелю) функция.
Тогда  называется переходной вероятностью, или вероятностью перехода.
называется переходной вероятностью, или вероятностью перехода.
Гипотеза H1. Существует семейство переходных вероятностей  для марковского процесса
для марковского процесса  со значениями в
со значениями в , такое, что Р – п.н. для любого
, такое, что Р – п.н. для любого 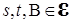
 (2)
(2)
Определение. Если -  марковский процесс со значениями в
марковский процесс со значениями в  и выполнено (2), то мы будем говорить, что задан марковский процесс с семейством переходных вероятностей
и выполнено (2), то мы будем говорить, что задан марковский процесс с семейством переходных вероятностей  .
.
Предложение 1. Пусть  - марковский процесс с семейством переходных вероятностей
- марковский процесс с семейством переходных вероятностей  .Тогда при
.Тогда при  справедливо
справедливо
 (3)
(3)
где  , ((3) называют уравнением Колмогорова–Чепмена).
, ((3) называют уравнением Колмогорова–Чепмена).
Доказательство. Доказательство утверждения предложения 1 проводится аналогично доказательству теоремы 1 гл. 2, поэтому его не приводим.
Соглашение H2: Пусть 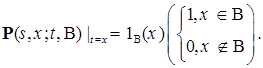
Определение. Марковским процессом в широком смысле (МПШ) называется такой процесс, что:
Бесплатная лекция: "3.6. Операционные системы ЛВС" также доступна.
i) принимает значения в ;
;
ii)  – семейство его переходных вероятностей;
– семейство его переходных вероятностей;
iii) выполнены гипотеза Н1 и соглашение Н2.
1.3. Закон входа МПШ. Пусть  и
и  , где
, где  - марковский процесс в широком смысле, тогда, в силу его марковского свойства, имеем:
- марковский процесс в широком смысле, тогда, в силу его марковского свойства, имеем:
 . (4)
. (4)
Равенство (4) называется законом входа для МПШ.




















