Сходимость последовательностей случайных величин по вероятности и почти наверное

                      § 6. Сходимость последовательностей случайных величин по вероятности и почти наверное.

6.1. Пусть на  задано последовательность случайных величин.

Определение. Последовательность случайных величин  называется сходящейся по вероятности к случайной величине , обозначается  или 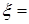, если для  при .

Теорема 14. Последовательность случайных величин  сходится по вероятности к случайной величине  тогда и только тогда, когда  при .

6.2. Определение. Последовательность случайных величин  называется сходящейся с вероятностью 1 к случайной величине , если , обозначается .

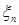
Следующее утверждение хорошо известно [1].

Теорема 15. Справедливы следующие утверждения.

1) Для того, чтобы 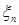, необходимо и достаточно, чтобы для любого 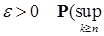 при .

2) Пусть 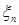, тогда .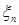

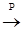
Рекомендуемые материалы

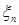
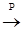
3) Пусть ., тогда существует подпоследовательность  такая, что .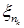

Замечание. Так как для любого    =
, то условие  является достаточным для сходимости .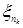

6.3. Теорема 16. (Егорова) Пусть 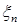. Тогда для любого  существует измеримое множество  такое, что > , причем на множестве сходимость  равномерная.

29. Характеристика зональных подтипов чернозёмов. - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Задача. Докажите самостоятельно утверждение теоремы 16.

6.4. Мы часто будем использовать следующее утверждение.

Лемма 17. (Бореля-Кантелли) Пусть   последовательность событий и . Если , то  Р(А) = 0.

Доказательство. В силу свойства вероятности имеем

Р(А) = .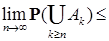

Доказательство закончено.