Что называют математическим ожиданием скалярной функции случайных величин. Сформулируйте и докажите основные свойства математического ожидания

Что называют математическим ожиданием скалярной функции случайных величин? Сформулируйте и докажите основные свойства математического ожидания.

Математическим ожиданием (средним значением) МХ дискретной случайной величины Х называют сумму произведений значений x_i случайной величины и вероятностей p_i = P{X=x_i}, с которыми случайная величина принимает эти значения: . При этом, если множество возможных значений случайной величины счетно, предполагается, что . В противном случае говорят, что МХ не существует.

Математическим ожиданием (средним значением) МХ непрерывной случайной величины называют интеграл . При этом предполагается, что .

Пусть  Y(X) –  функция от случайной  величины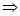

; ;  

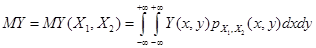
Для функций случайных величин математическое ожидание вычисляется аналогично.

Рекомендуем посмотреть лекцию "Содержание и введение".

Математическое ожидание удовлетворяет следующим свойствам:

1. Если случайная величина Х принимает всего одно значение с вероятностью 1, то МС=С.

2. M(aX+b) = aMX+b, где a, b – постоянные

3. M(X₁+X₂) = MX₁+MX₂

4. M(X₁X₂) = MX₁MX₂ для независимых случайных величин.

Доказательство состоит в раскрытии сумм и интегралов.