Фрактальные алгоритмы
Лекция 13
Фрактальные алгоритмы
Понятие фрактала
Латинское слово fractus означает "составленный из фрагментов". Фрактал можно определить как объект довольно сложной формы, получающийся в результате выполнения простого итерационного цикла. Итерационность, рекурсивность обусловливают такие свойства фракталов, как самоподобие – отдельные фрагменты фрактала похожи по форме на весь фрактал в целом.
В 1975 г. французский математик Бенуа Мандельброт издал книгу "The fractal Geometry of Nature".
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака – это не сферы, горы – не конусы, линии берега – не окружности, и кора не является гладкой, и молния не распространяется по прямой… Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности. Математики… предпочли все больше и больше отдаляться от природы, изобретая теории, которые не соответствуют ничему из того, что можно увидеть или почувствовать…" (Б.Мандельброт).
Мандельброт предложил сначала определение фрактала в таком виде: "Фракталом называется множество, размерность Хаусдорфа-Безиковича которого строго больше его топологической размерности". Затем он сформулировал более простое выражение: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому". Так что строгого и полного определения фракталов до сих пор не существует.
Выделяют несколько разновидностей фракталов: алгоритмические, геометрические и фракталы на основе метода IFS.
Алгоритмические фракталы
Рекомендуемые материалы
Фрактал Мандельброта. Мандельброт исследовал предельное (при k ® ¥) поведение последовательности комплексных чисел zk+1= zk2 + z0 , k=0, 1, 2, …; z0=c при различных значениях комплексных чисел c.
Последовательность zk с ростом числа итераций демонстрирует поведение двух типов в зависимости от выбора начальной точки z0. Ее элементы либо постепенно уходят в бесконечность, либо всегда остаются в определенной замкнутой области, совершая циклическое движение или сходясь в точку.
Математиками строго доказано, что если при некотором k модуль |zk|>rmin, где rmin=2 – минимальный радиус расходимости множества Мандельброта, то далее последовательность расходится.
Множество точек z0, для которых последовательность не расходится, называется множеством Мандельброта.
Графическая интерпретация множества Мандельброта удивительно красива и бесконечно разнообразна. Для ее получения используется следующий алгоритм. Комплексное число z=x+iy может быть изображено на плоскости точкой с координатами
(x, y). Изображение строится в некоторой прямоугольной области с разрешением n*m точек.
Формула итераций для фрактала Мандельброта выглядит следующим образом:
zk+1= zk2 + z0 , k=0, 1, 2, …
Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне для x0=(от -2,2 до 1) , для y0=(от -1,2 до 1,2) – начальные точки z0.
Для каждой начальной точки вычисляется количество k точек, попадающих в круг сходимости (k – число итераций). Условием завершения итераций является |zk|>2.
Суть алгоритма сводится к итерационному выводу точек, попадающих в круг сходимости для каждой начальной точки, в пределах заданного графического окна. Для каждого цикла итерации (для каждой начальной точки) выбирается свой цвет.
Если принять значения k для каждой начальной точки (x,y) в качестве высот некоторой поверхности в данной точке можно построить объемное изображение множества Мандельброта или его части, которое при специально подобранном освещении может выглядеть и как скала с плоской вершиной, и как водопад, и как горная пещера.
Типичный фрактал, каким является множество Мандельброта, представляет собой иерархический объект, состоящий из родительского тела в форме кардиоиды и многочисленных потомков, повторяющих форму предков, от которых они ответвляются. Само подобие элементов фрактала хорошо видно на его изображении.
Связность множества означает, что его элементы, даже самого малого размера, которые Мандельброт назвал "фрактальной пылью", не обособлены, а соединены тончайшими нитями в одно целое. Продолжая процесс увеличения пограничных областей, мы всюду видим бесконечное разнообразие форм, поражающих гармонией, великолепием и удивительным сходством с изображениями регулярно-хаотических явлений природы: молний, снежинок, ледяного узора, инея на ветвях деревьев, кораллов, паутины, солнечных протуберанцев, звездных скоплений и т.п.
Фрактал Джулио (Жюлио) внешне совсем не похож на фрактал Мандельброта, хотя формула итераций для этого фрактала почти полностью совпадает с формулой для фрактала Мандельброта:
zk+1= zk2 + c , k=0, 1, 2, …
где c – комплексная константа.
Если при генерации фрактала Мандельброта значение z0 каждый раз совпадает со значением в начальной точке на данном шаге итераций, то для фрактала Джулио значение c всегда одно и то же комплексное число.
В программе, (приведенной в приложении 2), построено изображение фрактала Джулио для c=0,36+i*0,36.
Итерационная формула для фрактала Ньютон имеет вид
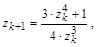
где z – также комплексные числа, причем z0=x+iy соответствует координатам точки изображения. Условием прекращения цикла итераций для фрактала Ньютон есть приближение значений |z4-1| к нулю.
Границы расчета: для x – от -1 до 1, для y – от -1 до 1.
Геометрические фракталы
Геометрическими названы фракталы, форма которых может быть описана как последовательность простых геометрических операций. Геометрические фракталы строятся на основе исходной фигуры – линии, полигона, полиэдра – путем ее дробления и выполнения аффинных и логических преобразований (объединения или исключения) полученных фрагментов.
 |
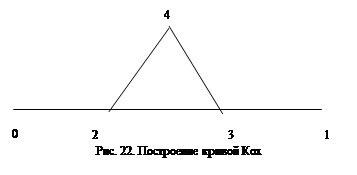Метод построения фрактального объекта может быть как итерационным, так и рекурсивным, причем рекурсивный чаще бывает богаче возможностями и проще в программировании. Например, кривая Кох становится фракталом в результате бесконечного количества итераций, в ходе которых выполняется деление каждого отрезка прямой на три части. На средней части
отрезка строится правильный треугольник, затем процесс повторяется для каждого из полученных отрезков, кроме среднего (рис. 22).
Алгоритм основан на рекурсивном вызове процедуры для каждого из полученных отрезков. Аналогичный алгоритм используется при построении фрактального треугольника.
Вообще алгоритм построения кривой Кох можно применить к любому многоугольнику или ломаной линии, запустив алгоритм построения кривой Кох для каждого из составляющих фигуру отрезков (в приложении 2 содержится программа построения кривой Кох и фрактального треугольника с помощью этой процедуры).
Площадные фракталы
Строительными элементами площадных геометрических фракталов служат плоские полигоны, чаще всего трех- и четырехугольники.
Самым знаменитым фракталом этого класса является треугольник Серпинского, строящийся путем разбиения треугольника – не обязательно равностороннего – средними линиями на четыре подобных треугольника, исключения центрального и рекурсивного разбиения угловых треугольников до получения площадных элементов желаемого или минимально видимого разрешения.
Алгоритм построения треугольника Серпинского (рис. 23).
1. 
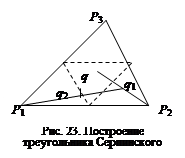Внутри исходного треугольника выбирается центральная точка:
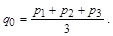
2. Задается число m итераций генерирования случайных точек.
3. В цикле для k от 1 до m:
– случайным образом выбирается номер n одной из вершин треугольника pn (генерируется случайное число в интервале от 1 до 3).
– вычисляется очередная точка qk в середине отрезка qk-1 pn:
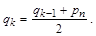
Благодаря выбору точки q0 внутри треугольника p1 p2 p3 центр отрезка q0 pn (точка q1) никогда не окажется внутри центрального треугольника, отмеченного на рисунке пунктиром. При достаточно большом числе итераций m генерируемые точки qk образуют случайный узор, предельная форма которого стремится к треугольнику Серпинского.
Следует отметить, что небольшое число начальных точек qk все-таки может попасть в запретные области. В частности, это случится при выборе точки q0 в центре треугольника p1 p2 p3 .
Аналогично треугольнику Серпинского может быть построена треугольная пирамида Серпинского.
Фракталы на основе метода IFS
Эту группу составляют фракталы, которые генерируются согласно методу "систем итеративных функций" – IFS (Iterated Functions Systems).
Данный метод может быть описан как последовательный итеративный расчет координат новых точек в пространстве:
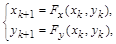
где Fx и Fy – функции преобразования координат, например аффинного преобразования. Эти функции и определяют форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов. Примером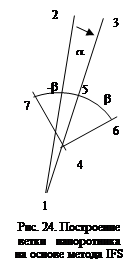 
такого фрактала является построение изображения листа папоротника (рис. 24).
Для начала итераций необходимо задать стартовые координаты линии – точки 1 и 2. На каждом шаге итераций рассчитываются координаты других точек.
Точка 3 получается поворотом точки 2 на угол a относительно центра в точке 1:
x3=(x2-x1)cosa-(y2-y1)sina+x1,
y3=(x2-x1)sina+(y2-y1)cosa+y1.
Если a=0, то ствол и все ветви прямые.
Находим точку 4. От нее будут распространяться ветви. Пусть соотношение длин отрезков 1-4 и 1-3 равно k (0<k<1). Тогда координаты точки 4: x4=x1(1-k)+kx3, y4=y1(1-k)+ky3.
Задаем длину и угол наклона ветвей, которые выходят из точки 4.
Найдем координаты точки 5: параметр k1 – соотношение длин отрезков 4-5 и 4-3 (0<k1<1):
x5=x4(1-k1)+k1x3,
y5=y4(1-k1)+k1y3.
Точка 6 получается поворотом точки 5 относительно точки 4 на угол b, а точка 7 – на угол (-b):
x6=(x5-x4)cosb-(y5-y4)sinb+x4;
y6=(x5-x4)sinb+(y5-y4)cosb+y4;
x7=(x5-x4)cosb+(y5-y4)sinb+x4;
y7=-(x5-x4)sinb+(y5-y4)cosb+y4.
После расчета опорных точек на каждом шаге рисуется отрезок 1-4. В зависимости от номера итерации цвет отрезка можно изменять.
Таким образом, фрактал задается как последовательность аффинных преобразований координат точек. Величины a, b, k, k1 – это параметры, которые описывают вид фрактала в целом. Они представляют собой константы на протяжении всего итеративного процесса. Это дает возможность в итерациях использовать только операции сложения, вычитания и умножения, если вычислить заранее значения:
A=cosa; B=sina; C=(1-k); D=k;
E=1-k1; F=k1; G=cosb; H=sinb.
Опишем рекурсивный алгоритм в виде процедуры ШАГ.
ШАГ(x1, y1, x2, y2, num)
Если (x1-x2)2+(y1-y2)2>lmin, то
Вычисляем координаты точек 3-7:
x3=(x2-x1)A - (y2-y1)B + x1
y3=(x2-x1)B + (y2-y1)A + y1
x4=x1C + x3D
y4=y1C + y3D
x5=x4E + x3F
y5=y4E + y3F
x6=(x5-x4)G - (y5-y4)H + x4
y6=(x5-x4)H + (y5-y4)G + y4
x7=(x5-x4)G + (y5-y4)H + x4
y7=-(x5-x4)H + (y5-y4)G + y4
Рисуем отрезок (x1, y1 - x4, y4)
ШАГ(x4, y4, x3, y3, num)
ШАГ(x4, y4, x6, y6, num+1)
ШАГ(x4, y4, x7, y7, num+1)
Для того чтобы нарисовать фрактал, необходимо вызвать процедуру ШАГ, установив соответствующие значения ее аргументов: ШАГ(x1,y1,x2,y2,0). Параметр num показывает степень детализации расчета дерева. Это значение можно использовать для прекращения итеративного процесса.
Завершение циклов итерации в нашем алгоритме происходит тогда, когда длина ветви становится меньше некоторой величины lmin.
Применение методов фрактальной графики
Метод IFS применяется не только для создания изображений. Барнсли и Слоан использовали его для эффективного сжатия графических изображений при записи в файлы. Основная идея такова: поскольку фракталы могут представлять очень сложные изображения с помощью простых итераций, то описание этих итераций требует значительно меньшего объема информации, чем соответствующие растровые изображения. При кодировании изображения необходимо решать обратную задачу: для изображения (или его фрагмента) подобрать соответствующие коэффициенты аффинного преобразования. Этот метод используется для записи цветных фотографий в файлы со сжатием в десятки и сотни раз без заметного ухудшения изображения. Формат таких графических файлов назван FIF (Fractal Image Format) и запатентован фирмой Iterated Sistems.
Фрактальный подход нашел широкое распространение во многих областях компьютерной графики, искусства и науки. Так, появилась теория фрактальных трещин, фрактальная механика древесно-полимерных композитов и другие отрасли.
В задачах КГ фрактальная технология получила наибольшее распространение при формировании объектов природного ландшафта: линии горизонта, неровных поверхностей, холмов, гор, каньонов и прочих нерегулярных образований. Построение основано на рекурсивном разбиении исходного объекта средними точками и смещении этих точек по методу управляемой случайности. Начальные объекты выбираются из простых геометрических фигур: отрезков, треугольников, прямоугольников, тетраэдров.
Фракталы широко применяют в растровых редакторах (Adobe Photoshop, Corel Painter), в векторной (Corel Draw, Adobe Illustrator) и трехмерной (Corel Bryce, 3Dmax) графике.
Существует программа FractalWorld российского программиста Юрия Щербакова, позволяющая строить изображения фракталов, описываемых системой двух уравнений второго порядка:
x[k+1] = a1x[k]2 + a2 y[k]2 + a3 x[k] y[k] +a4 x[k] + a5 y[k] +a6;
y[k+1] = b1x[k]2 + b2 y[k]2 + b3 x[k] y[k] +b4 x[k] + b5 y[k] +b6.
Задавая коэффициенты a и b, создают непохожие изображения. Цвет точки изображения соответствует количеству итераций. Критерий завершения итераций: x2+y2>10 для заданной стартовой точки.
Классификация фрактальных алгоритмов. По принципу преобразования элементов между итерациями фрактальные алгоритмы делятся на линейные (геометрические фракталы) и нелинейные (фрактал Мандельброта).
По характеру изменения объема пространства, занимаемого фрактальными объектами, между соседними уровнями рекурсии, фракталы делятся на аддитивные (увеличивающие объем занимаемого фракталом пространства) и субтрактивные (объем занимаемого фракталом пространства уменьшается – треугольник Серпинского).
Рекомендуем посмотреть лекцию "7 - Мышцы шеи и головы".
Свойства фракталов.
1. Прежде всего фрактал – это не линия или поверхность в виде привычных уравнений. Фракталы выражаются не в первичных геометрических формах, а в алгоритмах, которые трансформируются в геометрические формы с помощью компьютерной программы.
2. Характер большинства фрактальных алгоритмов преимущественно рекурсивный.
3. Теоретически глубина рекурсии фрактала бесконечна.
4. Независимо от природы и метода построения у всех фракталов есть одно важное общее свойство, характеризующее степень их раздробленности и предельные свойства. Это – фрактальная размерность. Согласно идее Мандельброта ее можно определить подсчетом числа элементов N, принадлежащих фрактальному множеству, при различных разрешениях d – минимальных линейных размерах элементов.
5. Размерность фрактала может быть дробной.
