Интеграл от ФКП

Интеграл от ФКП.

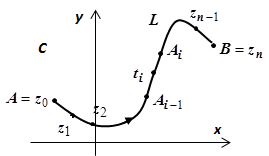
19.5.1.1. Определение. Пусть на комплексной плоскости С задана ориентированная кусочно-гладкая кривая , на которой определена функция .  Разобьём кривую точками   на  частей, на каждой из дуг  выберем произвольную точку , найдём  и составим интегральную сумму .

Предел последовательности этих сумм при , если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек , называется интегралом от функции  по кривой  и обозначается .

Теорема. Если функция  непрерывна на кривой , то она интегрируема по этой кривой.

Док-во. Распишем действительные и мнимые части всех величин, входящих в интеграл:   тогда  , и сумма  разобьётся на две . Каждая из этих сумм - интегральная сумма для действительных криволинейных интегралов второго рода, соответственно,  и . Если L - кусочно-гладкая кривая,  - непрерывна (тогда непрерывны её координатные функции  и ), то существуют пределы этих сумм при  - соответствующие криволинейные интегралы, следовательно, существует , и .

19.5.1.2. Свойства интеграла от ФКП. Мы доказали, что  выражается через два действительных криволинейных интеграла второго рода, поэтому он обладает всеми свойствами этих интегралов:

1.  - произвольные комплексные постоянные);

2.  - кривые без общих внутренних точек):

Рекомендуемые материалы

3.  - кривая, совпадающая с L, но проходимая в противоположном направлении;

4. Если l - длина кривой L, , то .

19.5.2. Интегральная теорема Коши. Это одна из основных теорем теории ФКП.

19.5.2.1. Теорема Коши для односвязной области. Если D - односвязная ограниченная область,  - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от  по L равен нулю: .

Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше,  ,  то, применяя к действительным криволинейным интегралам формулу Грина, получим , так как, по из условиям Коши-Римана . Символом G в доказательстве обозначена область, заключённая внутри контура L.

Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция , и имеющих общие начальную и конечную точки, интеграл  имеет одинаковое значение.

Доказательство полностью повторяет доказательство теоремы  Теоремы 1 раздела 16.3.3.5.1. Объединение  кривых - замкнутый контур, поэтому .

Оказывается, что справедлива и обратная теорема Морера: если функция  непрерывна в односвязной области D и интеграл по любому замкнутому кусочно-гладкому контуру, лежащему в D, равен нулю, то функция аналитична в области D.

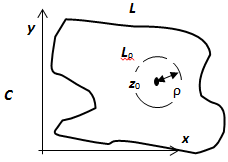
19.5.2.2. Теорема Коши для многосвязной области. Если функция  аналитична в замкнутой многосвязной ограниченной области , ограниченной контурами  (внешняя граница), , , …, , то  интеграл от , взятый по полной границе области , проходимой так, что область остаётся с одной стороны, равен нулю.

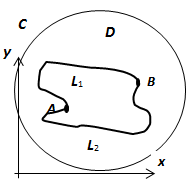
Доказательство и здесь воспроизводит доказательство формулы Грина для многосвязной области. Рассмотрим случай, когда граница области  (на рисунке область заштрихована) состоит из внешнего контура  и внутренних контуров L₁ и L₂. Соединим контур  разрезом FM с контуром L₁, разрезом BG - с контуром L₂ Область  с границей  односвязна, поэтому для неё справедлива интегральная теорема Коши:

. Интегралы по каждому из разрезов входят в этот общий интеграл дважды в противоположных направлениях и, как следствие, взаимно уничтожаются, поэтому остаются только интегралы по контурам, проходимым так, что область остаётся с одной стороны.

            В дальнейшем нам понадобится другая формулировка этой теоремы. Буквами без верхнего индекса будем обозначать контуры, проходимые против часовой стрелки, с верхним минусом  - по часовой. Мы доказали, что . Таким образом, интеграл по внешнему контуру равен сумме интегралов по внутренним контурам, при этом все контуры обходятся в одном направлении.

19.5.3. Первообразная аналитической функции. Если функция  аналитична в односвязной области D, то, как мы доказали, интеграл по кривой  зависит только от начальной и конечной точек и не зависти от формы кривой. Если зафиксировать начальную точку , то интеграл будет зависеть только от конечной точки z, поэтому можно написать .  Можно доказать (также, как мы доказывали существование потенциальной функции в односвязной области при выполнении условия ), что справедлива следующая

Теорема. Для любой аналитической в области D  функции  интеграл  является аналитической в D функцией, и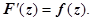

Любая функция  такая, что , называется первообразной функции . Любые две первообразные отличаются не более, чем на постоянную, поэтому , откуда при  получаем , или . Таким образом, для аналитических функций справедлива формула Ньютона-Лейбница, и основные приёмы интегрирования: .

19.6. Теория интегралов Коши.

            Мы доказали, что интеграл по замкнутому контуру от аналитической функции равен нулю. Сейчас мы испортим функцию в одной-единственной точке  введением множителя ; поразительно, какие глубокие выводы получил Коши для интегралов вида .

19.6.1. Интеграл  (). Возможные случаи: 1. Точка   лежит вне контура L. В этом случае подынтегральная функция аналитична в замкнутой области, ограниченной контуром, и интеграл равен нулю при любых целых n.

2. . И здесь подынтегральная функция аналитична, и интеграл равен нулю

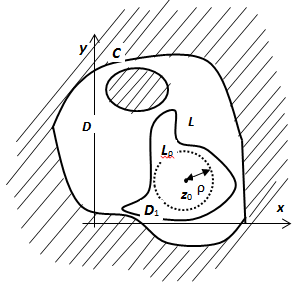
3. , и точка   лежит в области, ограниченной контуром L. Сведём интеграл по контуру L к более простому интегралу по окружности  с центром в точке  радиуса  столь малого, что окружность  лежит внутри L. В двухсвязной области, расположенной между L и , функция  аналитична, поэтому (следствие из 19.5.2.2. Теоремы Коши для многосвязной области) . Правый интеграл вычислим напрямую. Как и при вычислении любого криволинейного интеграла, мы должны параметризовать кривую. Если , то параметрические уравнения окружности радиуса  с центром в точке  имеют вид  Можно воспользоваться этими уравнениями, однако проще собрать их в комплексное число:  (таково параметрическое уравнение окружности на комплексной плоскости С), тогда , и .

4. . Выкладки в этом случае такие же, как и в предыдущем. вследствие периодичности первообразной.

Итак, мы доказали, что  при целом n неравен нулю в единственном случае - когда n = -1. В этом случае . Строго говоря, перебирая различные возможности, мы не рассмотрели вариант, когда точка   лежит на контуре L. В этом случае подынтегральная функция теряет определенность в точке , и необходима теория несобственных комплексных интегралов. В то же время очевидно, что если точка , находясь внутри контура L, то , если же  извне контура L, то . Вообще эти вопросы - предмет теории Сохоцкого.

19.6.2. Интегральная формула Коши.  Пусть  аналитична в области D и L - замкнутая кусочно-гладкая кривая, содержащаяся в D вместе с областью D₁, которую она ограничивает. Тогда для каждой точки  имеет место формула 

.

            Доказательство. Заметим, что в этой формуле функция в точке  портится как раз введением множителя . Доказательство очень похоже на доказательство того, что . Мы окружим точку  окружностью  радиуса  столь малого,  что на    мало отличается от : , тогда . Более строго, возьмём  столь малым, что окружность  радиуса  с центром в  лежит в D₁. Функция  аналитична в двусвязной области, заключенной между L и , поэтому (следствие из 19.5.2.2. Теоремы Коши для многосвязной области) . Распишем последний интеграл:  . Второй интеграл здесь равен . Первый интеграл а). не зависит от  ( действительно, подынтегральная функция аналитична в области между   и , где  - окружность радиуса , и по тому же следствию из 19.5.2.2. Теоремы Коши для многосвязной области ; б). .  Из этих утверждений а) и б) следует, что первый интеграл .

            Докажем утверждение б. Обозначим , при этом, вследствие непрерывности функции, . Оценим  по модулю (учитывая, что ):   . Утверждение доказано. Доказана и интегральная формула Коши: .

            Сформулируем несколько следствий из доказанной теоремы.

1. Значения аналитической в некоторой области функции полностью определяются её значениями на границе этой области. Этот факт можно сформулировать в виде теоремы о среднем. Возьмём  такое, что окружность  радиуса  с центром в  лежит в D_1. Тогда , и . Поэтому справедлива

2. Теорема о среднем. Значение аналитической функции в каждой точке z₀ равно среднему арифметическому её значений на любой окружности с центром в точке z₀.

Теорема доказана в предположении, что точка z₀ лежит внутри контура L. Если z₀ находится вне контура, то , так как подынтегральная функция аналитична в .

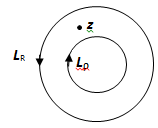
3. Формула справедлива и для многосвязной области, если под кривой L подразумевать полную границу области. В дальнейшем нам понадобится такой вариант:  аналитична в замкнутом кольце, ограниченном окружностями  и . Тогда для всех z, лежащих внутри кольца, ; при этом окружности проходятся так, что область остаётся слева. В последней формуле переобозначены переменные: .

19.6.3. Бесконечная дифференцируемость аналитической функции. Запишем интегральную формулу Коши в переменных z, t: . Продифференцируем эту формулу по z:  (на самом деле законность дифференцирования интеграла по параметру z  требует обоснования; мы примем этот факт без доказательства). Продолжим дифференцирование: ; , и вообще . Следовательно:

Если функция  имеет в каждой точке области D производную первого порядка ( т.е. аналитична в области D), то она имеет в этой области производную любого порядка (т.е. любая производная функции  аналитична в области D). Это свойство существенно отличает аналитические ФКП от дифференцируемых функций действительной переменной.

19.6.4. Применение интегральных формул Коши к вычислению интегралов. Запишем формулы Коши в виде , . С помощью этих формул вычисляются интегралы от функций вида , где  - аналитическая функция. Естественно, точка z₀ должна лежать внутри контура L (если она лежит вне контура, подынтегральная функция аналитична, и интеграл равен нулю).

Примеры: 1. . Здесь  лежит внутри круга , поэтому .

2. . Здесь внутри круга  лежит точка , поэтому  и .

3. . Здесь внутри круга  лежит точка , поэтому  и .

4. . Здесь внутри круга  лежат обе точки  и , но, по следствию из 19.5.2.2. Теоремы Коши для многосвязной области, .

5. . Для вычисления этого интеграла воспользуемся формулой  при : .

Ряд Тейлора. Пусть функция  аналитична в области D, . Обозначим L окружность с центром в z₀, принадлежащую области D вместе с ограниченным ею кругом. Тогда для любой точки z, лежащей внутри L, . Представим множитель  в виде суммы сходящейся геометрической прогрессии: (так как , то ) , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:  , так как . Итак,

                                               .

Ряд в правой части этого равенства - ряд Тейлора функции . Этот ряд абсолютно сходится внутри контура L, а в качестве L можно взять любую окружность, которая не выходит за пределы области D. Доказана

            Теорема о разложении функции в ряд Тейлора. Если функция  аналитична в области D, , то функция может быть разложена в ряд Тейлора по степеням . Этот ряд абсолютно сходится к  внутри круга , где r - расстояние от  до границы области D (до ближайшей к  точке, в которой функция теряет аналитичность). Это разложение единственно.

            Единственность разложения следует из того, что коэффициенты ряда однозначно выражаются через производные функции.

            19.6.1.1. Стандартные разложения. Для однозначных функций разложения в ряд Тейлора в принципе не могут отличиться от изучавшихся в прошлом семестре разложений:

1. ;

2. ;

3. ;

4. ;

5. ;

Все эти ряды сходятся к своим функциям на всей плоскости (при ). Для геометрических прогрессий имеют место формулы

6. .

7. ;

8. .

То, что эти ряды сходятся при , понятно. Ближайшие к центру разложения  точки, в которых функции теряют аналитичность (граница области D) - это точки , в которых соответствующие функции неопределены.

9. .

В действительном случае вообще было непонятно, почему этот ряд перестаёт сходиться к  при , ведь  определена на всей действительной прямой. В комплексном случае это проясняется - на окружности  расположены точки , в которых  не определена.

При разложении многозначных функций необходимо выделить однозначную ветвь. Обычно задают значение функции в одной точке. Например, , k - целое. Возьмём ту ветвь логарифма, для которой , т.е. главное значение логарифма . На этой ветви  , поэтому , и

10. .

Точка, в которой функция теряет аналитичность (она в этой точке вообще не определена) - это , поэтому ряд сходится при .

Теперь рассмотрим биномиальный ряд для функции . Это (при любом комплексном ) общая степенная функция, поэтому  (однозначная ветвь выделена тем, что взято главное значение логарифма); дальше находим производные: ; аналогично  ; и т.д.; , поэтому

11. .

. Ряд Лорана. Пусть функция  аналитична в кольце . Тогда для любой точки этого кольца ; при этом окружности проходятся так, что область остаётся слева (следствие 3 раздела 19.6.2. Интегральная формула Коши). Изменим в интеграле по внутренней окружности направление обхода на противоположное: . Интеграл по внешней окружности преобразуем так, как и при выводе формулы Тейлора: (так как , то ) , и ряд сходится абсолютно, поэтому его можно почленно интегрировать:

, где . Интеграл по внутренней окружности преобразуем аналогично, учитывая только, что на  :  . И здесь ряд сходится абсолютно, поэтому его можно почленно интегрировать:

 , где . Переобозначим , тогда форма коэффициентов ряда для  совпадёт с формой коэффициентов ряда для :  поэтому окончательно для интеграла по  получим . Докажем, что и контур для вычисления коэффициентов может быть взят один и тот же. Действительно, пусть  - кусочно-гладкий контур, расположенный в кольце , и точка  расположена внутри этого контура. По теореме Коши для многосвязной области ; , поэтому для любого n , и

.

           

Этот ряд (содержащий и положительные, и отрицательные степени ), называется рядом Лорана функции . Его часть, содержащая неотрицательные степени (), называется правильной; часть, содержащая отрицательные степени (), называется главной. Правильная часть, по самому своему построению, сходится в круге , главная - во внешности круга , поэтому весь ряд сходится в пересечении этих областей, т.е. в кольце . Так же, как и для ряда Тейлора, разложение в ряд Лорана единственно.

            Еще раз подчеркнем, что в ряд Лорана раскладывается функция, аналитическая в кольце, и ширина этого кольца определяется областью аналитичности функции, т.е. разложение теряет смысл, как только функция теряет аналитичность. Рассмотрим

Нули аналитической функции.

            Определение. Точка а называется нулём порядка k аналитической функции , если , но .

            Пример. Пусть . Точка  - нуль этой функции, так как . Найдём порядок нуля:  ,   . Первая отличная от нуля производная функции в точке  - пятая, поэтому эта точка - нуль пятого порядка функции .

            Теорема. Для того, чтобы аналитическая в точке а функция  имела в этой точке нуль k -го порядка, необходимо и достаточно, чтобы в окрестности этой точки функция  представлялась в виде , где  - аналитическая в точке а функция, и.

            Доказательство. Необходимость. Пусть точка а - нуль k-го порядка функции , т.е. , и . Тогда её разложение в ряд Тейлора имеет вид ,  где  - аналитическая (как сумма степенного ряда с тем же кругом сходимости, что у ряда для ) функция, .

            Достаточность. Пусть , где  - аналитическая функция, и. Находим производные этой функции по формуле Лейбница : ; ; ………………………….; ; , что и требовалось доказать.

            Из этой теоремы следует, что если многочлен  разложен на множители , то корни  являются нулями функции  кратностей, соответственно, .

            19.7.2. Изолированные особые точки.

            19.7.2.1. Определение. Точка а называется изолированной особой точкой функции , если существует окрестность этой точки, в которой  аналитична во всех точках, за исключением точки а.

            Рассмотрим разложение функции  в ряд Лорана  в окрестности изолированной особой точки а. При этом возможны следующие случаи.

1. Главная часть ряда Лорана отсутствует: .

В этом случае особая точка а называется устранимой.

2. Главная часть содержит конечное число членов:

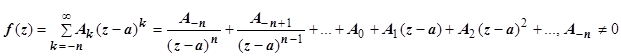
В этом случае особая точка а называется полюсом n-го порядка. Если n =1, полюс называется простым, в остальных случаях - кратным.

3. Главная часть содержит бесконечно много членов. В этом случае особая точка а называется существенно особой точкой.

19.7.2.2. Признаки особых точек по значению .

1. Для того, чтобы особая точка  была устранимой особой точкой функции , необходимо и достаточно, чтобы существовал конечный предел .

Док-во. Выпишем разложение  в ряд Лорана: . Очевидно, что  может быть конечным тогда и только тогда, когда отсутствуют члены с отрицательными степенями, т.е. отсутствует главная часть, т.е.  - устранимая особая точка. В этом случае .

2. Для того, чтобы особая точка  была полюсом функции , необходимо и достаточно, чтобы существовал бесконечный предел .

Докажем теорему, из которой следует это утверждение.

Теорема. Для того, чтобы особая точка  была полюсом n-го порядка функции , необходимо и достаточно, чтобы в некоторой окрестности этой точки  представлялась в виде , где  аналитическая в точке а функция, .

Док-во. Необходимость. Пусть  имеет в точке  была полюс n-го порядка, т.е. . Преобразуем это выражение: . Обозначим  сумму ряда, стоящего в скобках: .

Ряд Лорана функции  сходится в некотором кольце . Пусть точка  принадлежит этому кругу. Ряд для  сходится в этой точке, так как он отличается от сходящегося ряда для  только постоянным множителем ; по теореме Абеля ряд для  сходится в круге , и  аналитична в этом круге как сумма степенного ряда.

            Достаточность. Пусть , где  аналитическая в точке а функция, . Разложим  в ряд Тейлора: . Тогда , т.е. главная часть ряда Лорана функции  начинается с члена , где , т.е. точка  - полюс n-го порядка.

            Следствие. Точка  - полюс n-го порядка функции  тогда и только тогда, когда существует конечный .

            Теорема о связи нулей и полюсов. Функция  имеет в точке  - полюс n-го порядка тогда и только тогда, когда функция  имеет в этой точке нуль n-го порядка.

            Это теорема непосредственно следует из доказанной теоремы и теоремы предыдущего раздела. С её помощью легко определять порядок полюса. Так, мы доказали, что функция  имеет в точке 0 нуль пятого порядка. Поэтому функция  имеет в этой точке полюс пятого порядка.

3. Мы доказали, что в устранимой особой точке и в полюсе существует (конечный или бесконечный) . Поэтому в существенно особой точке этот предел существовать не может. Более того, верна теорема Пикара, которую мы приведём без доказательства:

В любой сколь угодно малой окрестности своей существенно особой точки функция  принимает (причём бесконечно много раз) любое конечное значение (за исключением, возможно, одного).

            19.7.3. Вычет аналитической функции в особой точке. Пусть функция  аналитична в области D за исключением точки a. Разложим  в окрестности этой точки в ряд Лорана: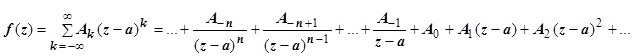

Коэффициент  называется вычетом функции  в точке а и обозначается . Если  - произвольный кусочно-гладкий замкнутый контур, расположенный в области D и содержащий внутри себя точку а, то, согласно общей формуле для коэффициентов ряда Лорана (см. 19.6.3. Ряд Лорана),  .

            19.7.3.1. Вычет в устранимой особой точке равен нулю.

Это следует из определения устранимой особой точки: главная часть ряда Лорана отсутствует, все коэффициенты с отрицательными индексами равны нулю, =0.

            19.7.3.2. Вычеты в полюсах.

            19.7.3.2.1. Если а - простой полюс функции , то .

                Док-во. Простой полюс - полюс первого порядка, поэтому разложение в ряд Лорана начинается с минус первой степени: . Тогда , и .

            19.7.3.2.2. Пусть , где  и  - аналитические в окрестности точки а функции. Если а - простой нуль функции , и , то .

            Док-во. Если а - простой нуль функции , и , то а – простой полюс функции . Тогда, по предыдущему утверждению,  .

19.7.3.2.3. Если а - полюс функции  n-го порядка, то .

            Док-во. Так как точка  - полюс n-го порядка функции , то. . Для того, чтобы удалить особенность в точке а, умножим  на : . Теперь, чтобы убрать первые члены этой формулы и добраться до , дифференцируем это произведение n-1 раз: ,

,

……………………………………………………………………………………………………………………….,

, , откуда и следует доказываемая формула.

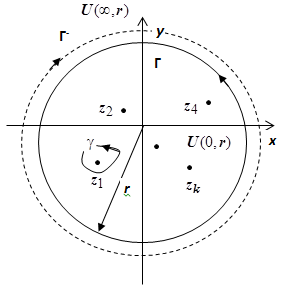
. Основная теорема о вычетах. Пусть функция  аналитична во всех точках ограниченной замкнутой области , границей которой является контур L, за исключением конечного числа особых точек , расположенных внутри L. Тогда .

            Док-во. Окружим каждую особою точку , контуром  таким, чтобы все контуры лежали в области D и не пересекались. В области, ограниченной контурами L, , функция аналитична, поэтому по 19.5.2.2. Теореме Коши для многосвязной области 

. По определению вычета, , следовательно, , что и требовалось доказать.

Примеры вычисления интегралов с помощью основной теоремы о вычетах.

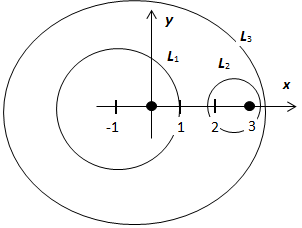
1. , где L - квадрат .

           

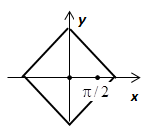
Обе особые точки подынтегральной функции -  и  - расположены внутри контура L, поэтому . Точка  -полюс первого порядка, . Точка  - нуль первого порядка и для числителя, и для знаменателя; докажем, что это - устранимая особая точка подынтегральной функции. Пусть , тогда , и , конечный предел существует, поэтому, действительно, это - устранимая особая точка, и . По основной теореме о вычетах .

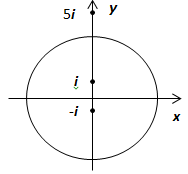
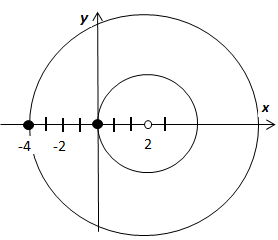
2. . В примере 2 раздела 19.7.3.4. Примеры нахождения вычетов мы доказали, что точка  - существенно особая точка подынтегральной функции, и , поэтому .

            3. . Здесь подынтегральная  функция  имеет две особых точки, расположенных в области, находящейся внутри контура:  (простой полюс) и  (полюс второго порядка). ,  ; .

            4. . Внутри контура расположена одна особая точка подынтегральной функции : . Это - существенно особая точка, поэтому для нахождения вычета необходимо найти коэффициент  разложения  в ряд Лорана в окрестности этой точки. ; .

, однако нет необходимости выписывать произведение этих рядов, достаточно только собрать те попарные произведения, которые дают минус первую степень переменной : . Легко сообразить, что это ряд для  при , т.е. , и .

            19.7.5. Бесконечно удалённая особая точка. Будем считать точку  особой точкой любой аналитической функции. В разделе 19.1.6. Окрестности точек плоскости  мы определили окрестности этой точки как внешности кругов с центром в начале координат: . Точка  является изолированной особой точкой аналитической функции , если в некоторой окрестности этой точки нет других особых точек этой функции. Для определения типа этой особой точки сделаем замену переменной , при этом точка  переходит в точку , функция  примет вид . Типом особой точки  функции  будем называть тип особой точки  функции . Если разложение функции  по степеням  в окрестности точки , т.е. при достаточно больших по модулю значениях , имеет вид , то, заменив  на , получим . Таким образом, при такой замене переменной главная и правильная части ряда Лорана меняются местами, и тип особой точки  определяется количеством слагаемых в правильной части разложения функции в ряд Лорана по степеням  в окрестности точки . Поэтому

1. Точка  - устранимая особая точка, если в этом разложении правильная часть отсутствует (за исключением, возможно, члена );

2. Точка  - полюс n-го порядка, если правильная часть заканчивается слагаемым ;

3. Точка  - существенно особая точка, если правильная часть содержит бесконечно много членов.

При этом остаются справедливыми признаки типов особых точек по значению : если  - устранимая особая точка, то этот предел существует и конечен, если  - полюс, то этот предел бесконечен, если  - существенно особая точка, то этот предел не существует (ни конечный, ни бесконечный).

Примеры: 1. . Функция уже является многочленом по степеням , старшая степень - шестая, поэтому  - полюс шестого порядка.

Люди также интересуются этой лекцией: Введение.

Этот же результат можно получить по-другому. Заменим  на , тогда . Для функции  точка  - полюс шестого порядка, поэтому для  точка  - полюс шестого порядка.

2. . Для этой функции получить разложение по степеням  затруднительно, поэтому найдём : ; предел существует и конечен, поэтому точка  - устранимая особая точка.

3. . Правильная часть разложения по степеням  содержит бесконечно много слагаемых, поэтому  - существенно особая точка. По другому этот факт можно установить исходя из того, что  не существует.

Вычет функции в бесконечно удалённой особой точке. Для конечной особой точки  , где  - контур, не содержащий других, кроме , особых точек, проходимый так, что область, им ограниченная и содержащая особую точку, остаётся слева (против часовой стрелке). Определим  аналогичным образом: , где  - контур, ограничивающий такую окрестность  точки , которая не содержит других особых точек, и проходимый так, что эта окрестность остаётся слева (по часовой стрелке). Таким образом, все остальные (конечные) особые точки функции должны находиться внутри контура . Изменим направление обхода контура : . По основной теореме о вычетах , где суммирование ведётся по всем конечным особым точкам. Поэтому, окончательно, , т.е. вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком. Как следствие, имеет место теорема о полной сумме вычетов: если функция  аналитична всюду в плоскости С, за исключением конечного числа особых точек , то сумма вычетов во всех конечных особых точках и вычета в бесконечности равна нулю.

            Отметим, что если  - устранимая особая точка, то вычет в ней может быть отличен от нуля. Так для функции , очевидно, ;  - единственная конечная особая точка этой функции, поэтому , несмотря на то, что , т.е.  - устранимая особая точка.