Приложение Л Собственные значения и векторы

П.12. Собственные значения и векторы

Для любой квадратной матрицы А можно найти такие скалярное число l и ненулевой вектор х, что удовлетворяется равенство

Ах=lх,                                                          (П.12.1)

где l - собственное значение матрицы А и х - её собственный вектор. (Иногда их называют характеристическими значением и вектором.) Выражение (П.12.1) называется уравнением собственных значений-векторов матрицы А. Заметим, что в нём вектор х преобразуется матрицей А в кратное самому себе, так что вектор Ах находится на линии, проходящей по вектору х из начала координат, как показано на рисунке П.12.

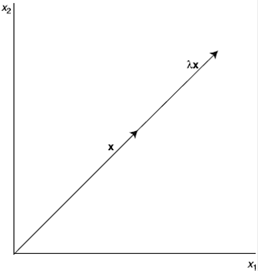
Рис. П.12 Собственный вектор х преобразуется в lх.

Чтобы найти l и х матрицы А, запишем (П.12.1) в виде

(А–lI)x=0.                                                    (П.12.2)

В силу (П.3.3), произведение (А–lI)x является линейной комбинацией столбцов матрицы (А–lI) и, в силу (П.4.1) и (П.12.2), эти столбцы линейно зависимы. Таким образом, квадратная матрица (А–lI) является вырожденной и, используя пункт 3 теоремы П.9.1, собственное значение l можно найти решением уравнения

Рекомендуемые материалы

det(А–lI)=0,                                                 (П.12.3)

которое известно как характеристическое уравнение.

Если А=А_nn, то это характеристическое уравнение имеет n корней, то есть матрица А имеет n собственных значений l₁, l₂,..., l_n. Собственные значения необязательно должны быть все разными или все отличными от нуля или даже все реальными числами. (Тем не менее, собственные значения симметричной матрицы являются реальными, см. теорему П.12.3.) Собственные значения l₁, l₂,..., l_n находятся из уравнения (П.12.3), а им соответствующие собственные векторы x₁, x₂,..., х_n можно найти из уравнения (П.12.2).

Если некоторое собственное значение равно 0, то соответствующий ему собственный вектор не равен 0. Чтобы убедиться в этом, заметим, что если l=0, то уравнение (А–lI)x=0 становится Ах=0, которое имеет решения для х, потому что A вырожденная и её столбцы линейно зависимы. [Матрица вырожденная потому, что она имеет нулевое собственное значение.]

Если умножить обе части уравнения (П.12.2) на скаляр k, то получим

k(А–lI)x=0,

что можно переписать в виде

(А–lI)kx=0.

Следовательно, если х - собственный вектор матрицы А, то kx также её собственный вектор. Таким образом, собственные векторы можно изменять умножением на скаляр. (Существует много векторов решений, потому что (А–lI) вырожденная, см. раздел П.8.) Отсюда длина вектора х произвольна, но его направление от начала координат является однозначно определённым, то есть отношения элементов вектора х^T= [x₁, x₂, ..., х_n] однозначны. Как правило, собственный вектор приводится к нормированному виду по формуле (П.10.3) и x^Tx=1.

Пример П.12.1. Для изучения собственных значений и векторов рассмотрим матрицу

А=.

В силу (П.12.3), характеристическим уравнением является

det(А–lI)=det=(1–l)(4–l)+2=0,

которое преобразуется к виду

l²–5 l+6=(l–3)(l–2)=0

с корнями l₁=3 и l₂=2.

Чтобы найти собственный вектор x₁, соответствующий l₁=3, используем (П.12.2)

(А–l₁I)x₁=0,

=,

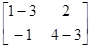
что можно записать в виде

–2x₁+2x₂=0

–x₁+x₂=0.

Второе уравнение является кратным первому и получается x₁=x₂. Вектор-решение можно записать с x₁=x₂=с как единичный вектор, умноженный на произвольную постоянную:

x₁===x₁=с.

Если для нормирования этого собственного вектора с =1/, то получаем

x₁=.

Аналогично, соответствующее собственному значению l₂=2 решение получаем в виде

x₂=.

□

Собственные значения и векторы функций от матриц

Если l - собственное значение матрицы A, а х – её собственный вектор, то для функции g(А) от матрицы A собственное значение этой функции g(А) задаётся функцией g(l), а х является собственным вектором функции g(А) и самой матрицы А. Покажем некоторые из таких функций:

1. Если l - собственное значение матрицы А, то сl - собственное значение матрицы сA, где с - произвольная постоянная с≠0. Это легко показать, умножая уравнение Ах=lх на с:

сАх=сlх.                                                      (П.12.4)

Заметим, что х - собственный вектор матрицы А, соответствующий собственному значению l, и х также собственный вектор матрицы сА, соответствующий собственному значению сl.

1. Если l - собственное значение матрицы А и х - соответствующий собственный её вектор, то сl+k - собственное значение матрицы сА+kI и х - собственный вектор матрицы сА+kI, где с и k - скалярные числа. Чтобы показать это, прибавим kх к обеим частям (П.12.4):

сАх+kх=сlх+kх.

(сА+kI)х=(сl+k)х.                                        (П.12.5)

Таким образом, сl+k - собственное значение матрицы сА+kI и х - соответствующий собственный вектор матрицы сА+kI. Заметим, что уравнение (П.12.5) неприменимо для суммы произвольных матриц А и В размеров nxn, то есть А+B не имеет собственного значения l_А+l_B, где l_А - собственное значение А и l_B - собственное значение B.

1. Если l - собственное значение матрицы А, то l² - собственное значение матрицы А². Это может быть показано путем умножения равенства Ах=lх слева на А:

А(Ах)=А(lх),

А²х=l(Ах)=l(lх)=l²х.                                (П.12.6)

Таким образом l² - собственное значение матрицы А² и х - соответствующий собственный вектор А². Это может быть распространено на любую степень А:

A^kx=l^kх;                                                        (П.12.7)

то есть, l^k - собственное значение матрицы A^k и х – соответствующий её собственный вектор.

1. Если l - собственное значение невырожденной матрицы А, то 1/l - собственное значение её обратной матрицы A^–1. Чтобы показать это умножим Ах=lх слева на A^–1

A^–1Ах=A^–1lх

х=lA^–1х

A^–1х=х.                                                      (П.12.8)

Таким образом, 1/l - собственное значение матрицы A^–1 и х - собственный вектор как матрицы А, так и матрицы A^–1.

1. Результаты, представленные уравнениями (П.12.4) и (П.12.7), могут быть использованы для получения собственных значений и векторов многочлена от A. Например, если l - собственное значение матрицы А, то для многочлена

(А³+4А²–3А+5I)x=А³x+4А²x–3Аx+5x

=l³x+4l²x–3lx+5x

=(l³+4l²–3l+5)x

выражение l³+4l²–3l+5 - собственное значение многочлена А³+4А²–3А+5I и х - соответствующий собственный его вектор.

Для определённых матриц последний результат может быть распространён на бесконечные ряды. Например, если l - собственное значение матрицы А, то в силу (П.12.5), 1–l - собственное значение I–А. Если матрица I–А невырожденная, то в силу (П.12.8), 1/(1–l) - собственное значение матрицы (I–А)^–1. Если –1<l<1, то бесконечный степенной ряд 1+l+l²+l³+... сходится и сумма его членов в области сходимости равна 1/(1–l) [Выгодский (2006) стр.661], то есть,

1/(1–l) =1+l+l²+l³+... .

Следовательно, если все собственные значения А удовлетворяют условию –1<l<1, то

(I–А)^–1=I+А+A²+A³+... .                                          (П.12.9)

Собственные значения и векторы произведений матриц

После уравнения (П.12.5) отмечено, что собственные значения суммы А+B матриц не имеют вид l_А+l_B, где l_А - собственное значение матрицs А и l_B - собственное значение матрицs В. Собственные значения произведения AB матриц также не имеют вид l_Аl_B. Однако собственные значения матрицы AB являются теми же, что и у матрицы ВА.

Теорема П.12.1. Если А=А_nn и В=В_nn или A=А_nр и В=В_рn, то (ненулевые) собственные значения произведения AB матриц являются теми же, что и у произведения ВА матриц. Если х - собственный вектор произведения АВ матриц, то Вх - собственный вектор произведения ВА матриц.

Доказательство:

(АВ–lI)х=0,

(ВАВ–lВ)х=0,

(ВА–lI)Вх=0.

□

Два дополнительных результата, включающие собственные значения произведений матриц, приведены в следующей теореме.

Теорема П.12.2. Пусть А=А_nn - любая матрица.

1. Если Р=Р_nn - любая невырожденная матрица, то A и P^–1AP имеют одинаковые собственные значения.

2. Если M=M_nn - любая ортогональная матрица, то A и M^ТAM имеют одинаковые собственные значения.

Доказательство:

0=det(P^–1AP–lI)=det(P^–1AP–lP^–1P)

=det[P^–1(A–lI)P]=det[(A–lI)PP^–1]

=det(A–lI).

Поэтому A и P^–1AP имеют одинаковые характеристические уравнения (П.12.3).

□

Собственные значения и векторы симметричных матриц

Два свойства собственных значений и векторов симметричной матрицы приведены в следующей теореме.

Теорема П.12.3. Пусть матрица А=А_nn симметричная.

1. Собственные значения l₁, l₂,..., l_n матрицы А реальные числа.

2. Собственные векторы x₁, x₂,..., х_n, соответствующие разным собственным значениям, могут быть выбраны взаимно ортогональными друг другу, то есть, x_i^Tх_j=0 для i≠j (i, j=1, 2, ..., n).

Доказательство: Докажем пункт 2 для случая, когда собственные значения l₁, l₂,..., l_n разные. Записывая уравнение (П.12.1) для векторов x_i и х_j, имеем Ах_i=l_iх_i и Ах_j=l_jх_j. Умножение их слева соответственно на x_j^T и x_i^T даёт

x_j^TАх_i=l_ix_j^Tх_i и x_i^TАх_j=l_jx_i^Tх_j.

Так как матрица А симметричная, то можно траспонировать обе части первого уравнения (x_j^TАх_i)^T=l_i(x_j^Tх_i)^T и получить x_i^TАх_j=l_ix_i^Tх_j. Это уравнение имеет такую же левую часть, как и второе уравнение, и поэтому их правые части тоже равны l_ix_i^Tх_j=l_jx_i^Tх_j, что можно представить в виде (l_i–l_j)x_i^Tх_j=0. Так как (l_i–l_j)≠0, то получаем x_i^Tх_j=0.

□

Если собственные векторы симметричной матрицы А нормированы и использованы в виде столбцов матрицы M, то по пункту 2 теоремы П.12.3 они могут быть выбраны все ортогональными друг другу и матрица M получается ортогональной. Эта матрица может быть использована для выражения матрицы А через её собственные значения и нормированные собственные векторы.

Теорема П.12.4. Если матрица А=А_nn симметричная с собственными значениями l₁, l₂,..., l_n и нормированными собственными векторами m₁, m₂,..., m_n, то она может быть представлена в виде

А=MLM^T                                                      (П.12.10)

=m_im_i^T,                                                 (П.12.11)

где L=диаг[l₁, l₂,..., l_n] и матрица M=[m₁, m₂,..., m_n] ортогональная. Любое выражение (П.12.10) или (П.12.11) часто называют спектральным разложением матрицы А.

Доказательство: По пункту 2 теоремы П.12.3 матрицу M можно сделать ортогональной. Тогда, в силу (П.10.5), имеем I=MM^T и его умножение слева на A даёт

A=AMM^T.

Теперь преобразуем это выражение разделением матрицы M по столбцам [m₁, m₂,..., m_n], чтобы получить

A=A[m₁, m₂,..., m_n]M^T

=[Am₁, Am₂,..., Am_n]M^T         [в силу (П.2.20)]

=[l₁m₁, l₂m₂,..., l_nm_n]M^T       [в силу (П.12.1)]

=MLM^T,                                                                               (П.12.12)

так как при умножение справа на L=диаг[l₁, l₂,..., l_n] столбцы матрицы M умножаются на элементы матрицы L [см. (П.2.22)]. Далее, записывая M^T в виде

M^T=[m₁, m₂,..., m_n]^T=,             [в силу (П.3.5)]

выражение (П.12.12) становится

A=[l₁m₁, l₂m₂,..., l_nm_n]

=l₁m₁m₁^T+l₂m₂m₂^T+...+l_nm_nm_n^T.

□

Следствие 1. Если матрица А симметричная, а M и L определены в теореме П.12.4, то с использованием матрицы M можно преобразовать А в диагональную:

M^TAM=L.                                                    (П.12.13)

Доказательство: В силу (П.12.10), А=MLM^T, а так как матрица M ортогональная, то умножая А=MLM^T слева на M^T и справа на M, получаем M^TАM=M^TMLM^TM=L.

□

Можно выразить также определитель и след квадратной матрицы А через её собственные значения.

Теорема П.12.5. Если матрица А=А_nn любая, имеющая собственные значения l₁, l₂,..., l_n, то

det(A)=                                                (П.12.14)

и

след(A)=.                                             (П.12.15)

Доказательство: [Schott (2016) стр.101] Характеристическое уравнение det(A–lI)=0 можно представить в виде многочлена

(–l)^п+α_п–1(–l)^п–1+…+α₁(–l)+α₀=0,                                      (П.12.16)

где коэффициенты α₀, α₁,..., α_п–1 скалярные числа. Сначала определим коэффициенты α₀ и α_п–1. Коэффициент α₀ можно определить, оценивая левую часть уравнения (П.12.16) при l=0. Таким образом, α₀=det(A–0I)=det(A). Для нахождения α_п–1, напомним, что по определению, определитель выражается в виде суммы членов для всех перестановок целых чисел (1, 2, ..., п). Так как α_п–1 - коэффициент перед (–l)^п–1, то для определения этого члена необходимо рассмотреть только те члены суммы, которые включают, по крайней мере, п–1 диагональных элементов (A–lI). Но каждый член в сумме является произведением п элементов матрицы (A–lI) с соответствующим знаком и элементами, выбранными по одному из каждой строки и каждого столбца матрицы (A–lI). Поэтому единственным членом в сумме, включающим, по крайней мере, п–1 диагональных элементов (A–lI), является член, представляющий произведение всех диагональных элементов. Так как этот член содержит чётное число перестановок, то знак члена +, и таким образом, α_п–1 - коэффициент перед (–l)^п–1 в произведении

(а₁₁–l)(а₂₂–l)...(а_пп–l),

что очевидно является а₁₁+а₂₂+...+а_пп или просто след(A). Теперь, чтобы связать α₀=det(A) и α_п–1=след(A) с собственными значениями матрицы А, отметим, что, так как l₁, ..., l_п - корни характеристического уравнения, который является полиномом от l порядка п, то следует, что

(l₁–l)(l₂–l)...(l_m–l)=0.

Выполняя умножение в левой части этого уравнения, а затем, приводя в соответствие соответствующие члены с теми, что в (П.12.16), находим det(A)= и след(A)=.

□

Эта теорема верна для любой квадратной матрицы. Она приведена здесь, так как её легко доказать для симметричной матрицы А с помощью теоремы П.12.4. Так, имеем det(A)=det(MLM^T) и, в силу (П.9.13), det(MLM^T)=det(M^TML)=det(L), а по (П.9.3) det(L)=.

Пример П.12.2. Для применения теоремы П.12.5 рассмотрим матрицу А из примера П.12.1

А=,

которая имеет собственные значения l₁=3 и l₂=2. Их произведение l₁l₂=6 такое же, как det(A)=4–(–1)(2)=6. Их сумма l₁+l₂=3+2=5 та же, что и след(А)=1+4=5.

□

Теорема П.12.6. Симметричная матрица, имеющая собственные значения равные 0 и 1, является идемпотентной.

Доказательство: По следствию 1 теоремы П.12.4 симметричная матрица А всегда может быть представлена в виде M^TAM=L, где L=диаг[l₁, l₂,..., l_n] диагональная матрица собственных значений матрицы А и матрица M ортогональная. Когда эти собственные значения равные 0 и 1, то имеем M^TAM=. По теореме П.12.4, A=MM^T, следовательно, АА=MM^TMM^T=MM^T=А, так как M^TM=I.

□

Теорема П.12.7. Если матрицы А и S симметричные и S положительно определённая, то имеющая собственные значения равные 0 и 1 матрица АS является идемпотентной.

Доказательство: Характеристическое уравнение det(АS–lI)=0 имеет решения равные 0 и 1. По теореме П.6.3 для некоторой невырожденной матрицы Р имеем S=P^ТР. Следовательно, уравнение det(P)det(АP^ТР–lI) det(P^–1)=0 имеет решения равные 0 и 1, то есть, det(РАP^Т–lI)=0 имеет решения равные 0 и 1. Отсюда РАP^Т имеет собственные значения равные 0 и 1 и является симметричной (РАP^Т)^T=РАP^Т. Следовательно по теореме П.12.6 матрица РАP^Т является идемпотентной, то есть РАP^ТРАP^Т=РАP^Т. А так как матрица Р невырожденная, то АP^ТРАP^ТР=АP^ТР, то есть, АSАS=АS, что и доказывает идемпотентность матрицы АS.

□

Собственные значения и векторы определённых матриц

Собственные значения l₁, l₂,..., l_n положительно и неотрицательно определённых матриц (раздел П.6) соответственно положительные и неотрицательные.

Теорема П.12.8. Пусть матрица А=А_nn имеет собственные значения l₁, l₂,..., l_n.

1. Если А положительно определённая, то l_i>0 (i =1, 2,..., n).

2. Если А неотрицательно определённая, то l_i≥0. Число собственных значений l_i больших 0 равно рангу матрицы А.

Доказательство:

1. Для любого собственного значения l_i имеем Ax_i=l_ix_i. Умножая слева на x_i^T, получаем

x_i^TAx_i=l_ix_i^Tx_i и l_i=(x_i^TAx_i)/(x_i^Tx_i)>0.

Во втором выражении квадратичная форма x_i^TAx_i положительная, так как матрица A положительно определённая, и x_i^Tx_i положительно, потому что x_i≠0.

2. В доказательстве первого пункта, если А неотрицательно определённая, то x_i^TAx_i≥0, в то время как x_i^Tx_i>0. По следствию 1 теоремы П.12.4 имеем M^TAM=L, где L=диаг[l₁, l₂,..., l_n]. Так как матрица M ортогональная и невырожденная, то по пункту 2 теоремы П.4 ранг матрицы L равен рангу матрицы А. Так как L диагональная, то её ранг равен числу ненулевых элементов в диагонали, то есть, числу ненулевых собственных значений [Rao, Rao (1998) стр.181].

□

Если матрица А положительно определённая, то можно найти её квадратный корень следующим образом. Поскольку собственные значения матрицы А положительные, то в её спектральном разложении по формуле (П.12.10) можно заменить собственные значения l_i их квадратными корнями  чтобы получить

А^1/2=ML^1/2M^T,                                              (П.12.17)

где L^1/2=диаг[,,...,]. Матрица А^1/2 симметричная и произведение

А^1/2А^1/2=(А^1/2)²=A.                                        (П.12.18)

Люди также интересуются этой лекцией: 5.5. Контркультура и субкультура.

Теорема П.12.9. Симметричная матрица А=А_nn ранга r может быть записана в виде LL^T, где матрица L=L_nr ранга r, то есть, имеет полный ранг по столбцам.

Доказательство: Для некоторой ортогональной матрицы М можно написать

МАМ^T==,

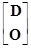
где матрица D=D_rr диагональная. Следовательно,

А=М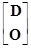^TМ=LL^T,

где L^T=М размеров rxn и полного ранга по строкам, то есть L=L_nr полного ранга по столбцам. Заметим также, что, хотя LL^T=А и L^TL=D², матрица L^T является действительной только когда А неотрицательно определённая, то есть, только когда ненулевые элементы матрицы D² положительные.