Доверительные интервалы и интервалы предсказания
9.5. Доверительные интервалы и интервалы предсказания
В разделе 6.5 показано, как находить доверительные интервалы отдельных параметров простой модели. В этом разделе для модели с нормированными факторами находится доверительная область вектора b параметров, доверительные интервалы для отдельных параметров и линейной комбинации aTb параметров, для математического ожидания E(у) переменной отклика, для дисперсии s2 и интервалы предсказания будущих наблюдений. Полагается, что во всём разделе вектор у имеет нормальное распределение Nn(Xb, s2I).
Доверительная область вектора параметров
Если в (9.3.14) матрица C равна единичной матрице I и вектор t равен b, то q=р и получаем величину  , имеющую центральное распределение F(р, п–р). Зная, что s2=SE/(п–р), можно сделать вероятностное утверждение
, имеющую центральное распределение F(р, п–р). Зная, что s2=SE/(п–р), можно сделать вероятностное утверждение
Рr[( –b)ТXТX(
–b)ТXТX( –b)/(рs2)≤Fкр]=1–α,
–b)/(рs2)≤Fкр]=1–α,
где Fкр - критическое значение случайной переменной с распределением F(р, п–р) и интегральной вероятностью 1–α на интервале от 0 до Fкр. На основе этого утверждения 100(1–α)% совместная доверительная область для элементов b0, b1, ..., bр–1 вектора b определяется состоящей из всех значений элементов этого вектора, удовлетворяющих условию
( –b)ТXТX(
–b)ТXТX( –b)≤рs2Fкр. (9.5.1)
–b)≤рs2Fкр. (9.5.1)
Для р=2 эта область может быть построена в двух измерениях в виде эллипса. Для р>2 данная выражением (9.5.1) эллипсоидная область является громоздкой для интерпретирования и описания. Поэтому рассматриваются интервалы для отдельных параметров, как показано в разделе 6.5.
Доверительные интервалы для отдельных параметров
Рекомендуемые материалы
Если параметр bj≠0, то в числителе выражения (9.3.6) можно вычесть bj, так что получается статистика tj= , имеющая центральное распределение t. Знаменатель этого выражения s
, имеющая центральное распределение t. Знаменатель этого выражения s часто называют среднеквадратической ошибкой результата
часто называют среднеквадратической ошибкой результата  оценки параметра модели, то есть се(
оценки параметра модели, то есть се( )=s
)=s .
.
Считая, что вероятность Pr[–tα/2(п–р)≤ ≤tα/2(п–р)]=1–α, и преобразуя неравенство в скобках относительно bj, получаем
≤tα/2(п–р)]=1–α, и преобразуя неравенство в скобках относительно bj, получаем
Рr[ –tα/2(п–р)s
–tα/2(п–р)s ≤bj≤
≤bj≤ +tα/2(п–р)s
+tα/2(п–р)s ]=1–α
]=1–α
или
Рr[ –tα/2(п–р)се(
–tα/2(п–р)се( )≤bj≤
)≤bj≤ +tα/2(п–р)се(
+tα/2(п–р)се( )]=1–α.
)]=1–α.
Следовательно, 100(1–α)% доверительный интервал для параметра bj находится из выражения
 ±tα/2(п–р)s
±tα/2(п–р)s . (9.5.2)
. (9.5.2)
Заметим, что доверительная вероятность 1–α имеет место только для одного доверительного интервала и одного из параметров. Доверительные интервалы для всех рассматриваемых одновременно р параметров с общей доверительной вероятностью 1–α даются, например, в книге [Rencher, Schaalje (2008) cтр. 215-217].
Пример 9.5.1. Вычислим 95% доверительные интервалы для всех параметров моделей из примера 8.3. Матрица (XТX)–1 и вектор оценки параметров модели, матрица которой содержит неортогональные между собой вектор-столбцы нормированных значений факторов, имеют соответственно вид:
(XТX)–1= и
и  =
= .
.
Матрица (XоТXо)–1 и вектор оценки параметров модели, матрица которой содержит все ортогональные между собой вектор-столбцы нормированных значений факторов, имеют соответственно вид:
(XоТXо)–1= и
и  =
= .
.
Результат s=144,711 оценки получается по формуле s= . Критическое значение tα/2(п–р) находится по таблице [Box, Draper (2007) стр.745] или с использованием программы Mathcad. График функции плотности вероятности случайной переменной, имеющей распределение t c п–р=11 степенями свободы, показан на Рис.9.5.1.
. Критическое значение tα/2(п–р) находится по таблице [Box, Draper (2007) стр.745] или с использованием программы Mathcad. График функции плотности вероятности случайной переменной, имеющей распределение t c п–р=11 степенями свободы, показан на Рис.9.5.1.
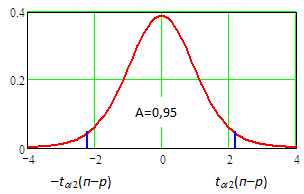
Рис.9.5.1. График функции плотности вероятности случайной переменной с распределением t(11).
Как и функция плотности вероятности нормального распределения она симметрична относительно 0. Критические значения +tα/2(п–р) и –tα/2(п–р) вычисляются на основе того, что за их пределами площадь обеих хвостовых частей под кривой функции равна (1–А)/2. Тогда, если выбирается доверительная вероятность A=0,95, то 95% площади под кривой функции будет находиться между значениями –tα/2(п–р) и tα/2(п–р). Критическое значение –tα/2(п–р)= –2,201 вычисляется с использованием встроенной в Mathcad обратной кумулятивной функции распределения t по формуле
–tα/2(п–р)=qt[(1–А)/2, (п–р)].
И из-за симметрии кривой функции плотности вероятности значение tα/2(п–р)=2,201.
Таким образом, по формуле (9.5.2) вычисляются 95% доверительные интервалы для всех параметров моделей. Результаты расчётов сведены в таблицу 9.5.1. Из этой таблицы видно, что для модели с матрицей, содержащей все ортогональные между собой столбцы, 95% доверительный интервал параметра b1 меньше, чем доверительный интервал этого параметра для модели с матрицей, содержащей неортогональные между собой столбцы.
Таблица 9.5.1. Доверительные интервалы для параметров двух моделей.
| Матрица модели с неортогональными столбцами | Матрица модели с ортогональными столбцами | ||||
| Параметры | 95% доверительные интервалы | Параметры | 95% доверительные интервалы | ||
| b0 | 1165 | 1335 | b0 | 1165 | 1335 |
| b1 | 87,035 | 257,964 | b1 | 82,899 | 252,637 |
| b2 | –139,781 | 31,148 | b2 | –139,781 | 31,148 |
□
Доверительный интервал для линейной комбинации параметров
Если линейная комбинация aTb≠0, то в числителе выражения (9.3.4) можно вычесть aTb из aT и получить статистику
и получить статистику
FL= ,
,
имеющую распределение F(1, п–р). Тогда, в силу (5.4.9), статистика
tL= (9.5.3)
(9.5.3)
имеет распределение t(п–р) и 100(1–α)% доверительный интервал для одной линейной комбинации aTb получается в виде
aT ±tα/2(п–р)s
±tα/2(п–р)s . (9.5.4)
. (9.5.4)
Доверительный интервал для математического ожидания Е(у)
Пусть вектор-строка xс представляет конкретный набор значений элементов вектора-строки хс= [1, x1, x2,..., х(р–1)] факторов, являющейся одной из строк матрицы X. Пусть у - переменная отклика, соответствующая вектору-строке xс значений влияющих на неё факторов. Тогда модель для этого опыта принимает вид
у=xсb+e
и, если допустить, что функция модели правильна, так что Е(e)=0, то
E(у) =xсb. (9.5.5)
Необходимо найти доверительный интервал для математического ожидания E(у) случайной переменной (у) отклика при заданных значениях элементов вектора xс.
По следствию 1 теоремы 7.2.4 несмещенной оценкой математического ожидания E(у) с наименьшей дисперсией является
 (у)=xс
(у)=xс . (9.5.6)
. (9.5.6)
Так как (9.5.5) и (9.5.6) имеют соответственно вид xсb и xс , то в силу (9.5.4), 100(1–α)% доверительный интервал математического ожидания E(у) =xсb получается в виде
, то в силу (9.5.4), 100(1–α)% доверительный интервал математического ожидания E(у) =xсb получается в виде
xс ±tα/2(п–р) s
±tα/2(п–р) s . (9.5.7)
. (9.5.7)
Доверительная вероятность 1–α для интервала в (9.5.7) имеет место только для одного набора значений элементов вектора xс.
Пример 9.5.2. Положим надо найти 95% доверительный интервал математического ожидания E(у) коэффициента усиления транзистора для данных примера 7.1 при x1=225 и x2=4,30 в опытах 9 и 12. В соответствии с выполненным в примере 8.3 нормированием факторов, нормированные их значения x1=0,597 и x2=–0,146, а вектор-строка xс= [1 0,597 –0,146].
Для модели с неортогональными столбцами её матрицы оценка ожидаемого значения переменной отклика  (у)=xс
(у)=xс =1361, а для модели с ортогональными столбцами её матрицы
=1361, а для модели с ортогональными столбцами её матрицы  (уо)=xс
(уо)=xс =1358. Для расчёта доверительных интервалов используем матрицы (XТX)–1 и (XоТXо)–1 из примера 9.5.1, а также s=144,711 и tα/2(п–р)=2,201. Для модели с неортогональными столбцами её матрицы математическое ожидание E(у)=xсb и для модели с ортогональными столбцами её матрицы математическое ожидание E(уо)=xсbо. В силу (9.5.7), 95% доверительные интервалы для них получаются соответственно в виде 1260≤xсb≤1461 и 1258≤xсbо≤1458. Длина 95% доверительного интервала для модели с ортогональными столбцами её матрицы равна 199,845 и она меньше длины 95% доверительного интервала для модели с неортогональными столбцами её матрицы равной 201,148. Это ещё раз подтверждает отмеченную в разделе 6.5 предпочтительность ортогональных планов.
=1358. Для расчёта доверительных интервалов используем матрицы (XТX)–1 и (XоТXо)–1 из примера 9.5.1, а также s=144,711 и tα/2(п–р)=2,201. Для модели с неортогональными столбцами её матрицы математическое ожидание E(у)=xсb и для модели с ортогональными столбцами её матрицы математическое ожидание E(уо)=xсbо. В силу (9.5.7), 95% доверительные интервалы для них получаются соответственно в виде 1260≤xсb≤1461 и 1258≤xсbо≤1458. Длина 95% доверительного интервала для модели с ортогональными столбцами её матрицы равна 199,845 и она меньше длины 95% доверительного интервала для модели с неортогональными столбцами её матрицы равной 201,148. Это ещё раз подтверждает отмеченную в разделе 6.5 предпочтительность ортогональных планов.
□
Интервал предсказания будущего наблюдения
В разделе 7.3 показано, что линейная модель может использоваться для предсказания значений переменной отклика при новых значениях факторов. Пусть строка x0с= [1, x01, x02,..., х0(р–1)] представляет новый набор значений элементов строки хс=[1, x1, x2,..., х(р–1)] факторов. Строка x0с не является одной из строк матрицы X используемой для оценки параметров модели. Однако если значения элементов этой строки сильно отличаются от значений соответствующих элементов строк матрицы X, то предсказание с применением результата оценки параметров модели с матрицей Х может быть неверным.
Доверительный интервал предсказываемого значения переменной y0 отклика, соответствующего строке x0с значений факторов, называется интервалом предсказания. В этом случае говорят об интервале предсказания, а не о доверительном интервале, так как y0 является случайной переменной отклика, а не параметром. Чтобы быть на 100(1–α)% уверенным, что интервал предсказания содержит предсказываемое значение переменной y0, очевидно, что этот интервал должен быть больше доверительного интервала для ожидаемого значения E(y).
Для предсказания используется модель y0=x0сb+e и предсказываемое значение переменной y0 находится по формуле  =x0с
=x0с , что является также результатом оценки ожидаемого значения E(у0)=x0сb. Случайные величины y0 и
, что является также результатом оценки ожидаемого значения E(у0)=x0сb. Случайные величины y0 и  независимы, так как значение переменной y0 предсказываемого наблюдения считается независимым от п наблюдаемых значений переменных отклика, используемых для вычисления
независимы, так как значение переменной y0 предсказываемого наблюдения считается независимым от п наблюдаемых значений переменных отклика, используемых для вычисления  . Поэтому дисперсия разности y0–
. Поэтому дисперсия разности y0– получается в виде
получается в виде
D(y0– )=D(y0–x0с
)=D(y0–x0с )
)
=D(x0сb+e –x0с ).
).
Так как x0сb является постоянной величиной, то имеем
D(y0– ) =D(e)+D(x0с
) =D(e)+D(x0с )
)
=s2+s2x0с(XТX)–1x0сТ
=s2[1+x0с(XТX)–1x0сТ], (9.5.8)
что можно оценить выражением s2[1+x0с(XТX)–1x0сТ]. Математическое ожидание Е(y0– ) =0, так как Е(e)=0 и Е(
) =0, так как Е(e)=0 и Е( )=b, а результат s2 оценки дисперсии не зависит от y0 и
)=b, а результат s2 оценки дисперсии не зависит от y0 и  =x0с
=x0с . Таким образом, статистика tу в виде
. Таким образом, статистика tу в виде
tу= (9.5.9)
(9.5.9)
имеет распределение t(п–р). Что с вероятностью 1–α её значения находится в интервале между –tα/2(п–р) и tα/2(п–р) можно записать в виде
Pr[–tα/2(п–р)≤ ≤tα/2(п–р)]=1–α.
≤tα/2(п–р)]=1–α.
Для получения 100(1–α)% интервала предсказания значений переменной y0 неравенство в квадратных скобках преобразуем к виду
 –tα/2(п–р)s
–tα/2(п–р)s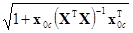 ≤y0≤
≤y0≤ +tα/2(п–р)s
+tα/2(п–р)s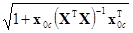
и, учитывая, что  =x0с
=x0с , получаем выражение для этого интервала
, получаем выражение для этого интервала
x0с ±s
±s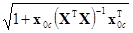 tα/2(п–р). (9.5.10)
tα/2(п–р). (9.5.10)
Заметим, что доверительная вероятность 1–α для интервала предсказания (9.5.10) имеет место только для одного набора значений элементов строки x0с.
В выражении 1+x0с(XТX)–1x0сТ второй член x0с(XТX)–1x0сТ, как правило, гораздо меньше единицы (при условии, что р гораздо меньше чем п), так как дисперсия оценки  =x0с
=x0с гораздо меньше дисперсии переменной y0. [Например, если бы XТX была диагональной и значения элементов x0 были в области охватываемой значениями элементов строк матрицы X, то x0с(XТX)–1x0сТ была бы суммой из р слагаемых, каждое из которых вида x0j2/
гораздо меньше дисперсии переменной y0. [Например, если бы XТX была диагональной и значения элементов x0 были в области охватываемой значениями элементов строк матрицы X, то x0с(XТX)–1x0сТ была бы суммой из р слагаемых, каждое из которых вида x0j2/ , что порядка 1/п.] Таким образом, интервалы предсказания переменной y0, как правило, значительно больше доверительных интервалов математического ожидания E(у)=xсb.
, что порядка 1/п.] Таким образом, интервалы предсказания переменной y0, как правило, значительно больше доверительных интервалов математического ожидания E(у)=xсb.
Пример 9.5.3. Положим надо найти 95% интервал предсказания математического ожидания E(у0) коэффициента усиления транзистора для данных примера 7.1 при x01=225 и x02=4,36. В соответствии с выполненным в примере 8.3 нормированием факторов, нормированные их значения соответственно x01=0,597 и x02=0,090, а строка x0с= [1 0,597 0,090].
Для модели с неортогональными столбцами её матрицы результат оценки математического ожидания переменной отклика  (у0)=x0с
(у0)=x0с =1348, а для модели с ортогональными столбцами её матрицы
=1348, а для модели с ортогональными столбцами её матрицы  (у0о)=x0с
(у0о)=x0с =1345. Для расчёта интервалов предсказания используем матрицы (XТX)–1 и (XоТXо)–1 примера 9.5.1, а также s=144,711 и tα/2(п–р)=2,201. Для модели с неортогональными столбцами её матрицы математическое ожидание E(у0) =x0сb, а для модели с ортогональными столбцами её матрицы E(у0) =x0сbо. В силу (9.5.10), они имеют 95% интервалы предсказания соответственно в виде: 1014≤x0сb≤1681 и 1011≤x0сbо≤1679. Заметим, что эти интервалы предсказания для у0 длинами соответственно 667,193 и 667,339 гораздо больше длин доверительных интервалов для Е(у) в примере 9.5.2.
=1345. Для расчёта интервалов предсказания используем матрицы (XТX)–1 и (XоТXо)–1 примера 9.5.1, а также s=144,711 и tα/2(п–р)=2,201. Для модели с неортогональными столбцами её матрицы математическое ожидание E(у0) =x0сb, а для модели с ортогональными столбцами её матрицы E(у0) =x0сbо. В силу (9.5.10), они имеют 95% интервалы предсказания соответственно в виде: 1014≤x0сb≤1681 и 1011≤x0сbо≤1679. Заметим, что эти интервалы предсказания для у0 длинами соответственно 667,193 и 667,339 гораздо больше длин доверительных интервалов для Е(у) в примере 9.5.2.
□
Доверительный интервал для дисперсии
По пункту 2 теоремы 7.3.4 величина (п–р)s2/s2 имеет распределение c2(п–р). Поэтому вероятностное высказывание, что её значения находятся в интервале между критическими значениями c21–α/2(п–р) и c2α/2(п–р), можно представить в виде
Pr[c2α/2(п–р)≤ ≤c21–α/2(п–р)]=1–α, (9.5.11)
≤c21–α/2(п–р)]=1–α, (9.5.11)
где c2α/2(п–р) - меньшее α/2-процентное критическое значение распределения хи-квадрат и c21–α/2(п–р) - большее 1–α/2-процентное критическое значение. Преобразование неравенства в квадратных скобках относительно s2 приводит к неравенству
(п–р)s2/c21–α/2(п–р)≤s2≤(п–р)s2/c2α/2(п–р), (9.5.12)
являющимся 100(1–α)% доверительным интервалом для дисперсии. Отсюда 100(1–α)% доверительный интервал стандартного отклонения s дается неравенством
[(п–р)s2/c21–α/2(п–р)]1/2≤s≤[(п–р)s2/c2α/2(п–р)]1/2. (9.5.13)
Пример 9.5.4. В формулах расчёта доверительных интервалов (9.5.7) и интервалов предсказания (9.5.10) используется результат оценки стандартного отклонения s. Найдём доверительный интервал этого стандартного отклонения для данных из примеров 9.5.2 и 9.5.3.
На Рис.9.5.2 показано, что в отличие от распределения t распределение c2(11) несимметричное. Поэтому критические значения c21–α/2(п–р) и c2α/2(п–р) необходимо вычислять отдельно. Для этого используется то, что площадь хвоста под кривой функции плотности вероятности слева от c2α/2(п–р) равна (1–А)/2, а площадь под кривой функции плотности вероятности слева от c21–α/2(п–р) равно (1–А)/2+А=(1+А)/2. Например, если для рассматриваемых данных п–р=11 и доверительную вероятность А принять равной 0,95, то, используя встроенную в Mathcad обратную кумулятивную функцию распределения c2, меньшее критическое значение c20,025(11)=3,816 рассчитывается по формуле
c20,025(11) =qchisq[(1–А)/2, 11],
а большее критическое значение c20,975(11)=21,920 рассчитывается по формуле
c20,975(11) =qchisq[(1+А)/2, 11].
Следовательно, выражение (9.5.13) вычисления доверительного интервала стандартного отклонения для рассматриваемых данных принимает вид
[11s2/c20,975(11)]1/2≤s≤[11s2/c20,025(11)]1/2
и в результате вычисления имеем 102,512≤s≤245,701.
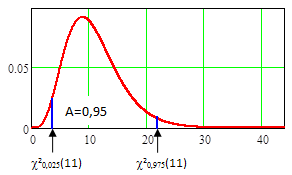
Рис.9.5.2. График функции плотности вероятности случайной переменной с распределением c2(11).
□
Упражнения
9.1. Покажите, что Hc[I–Е/n]=Hc, как и в (9.1.4) пункта 1 теоремы 9.1.1, где матрица Hc=Xc(XcТXc)–1XcТ.
9.2. Покажите, что среднее квадратичное SRс/(p–1) в таблице 9.1.1 имеет математическое ожидание E[SRс/(p–1)]=s2+b1ТX1ТX1b1/(p–1). Примените следующие два подхода:
(a) Используйте теорему 5.2.1.
(б) Используйте параметр не центральности в (5.19).
9.3. Разработайте процедуру проверки гипотезы H0: b=0 для модели у=Xb+e, где вектор у имеет распределение Nn(Xb, s2I). (В начале раздела 9.1 было отмечено, что эта гипотеза не имеет большого практического интереса, потому что включает в себя b0=0.) Используйте выражение yТy= (yТy– ТXТy)+
ТXТy)+ ТXТy и действуйте следующим образом:
ТXТy и действуйте следующим образом:
1. Покажите, что  ТXТy=yТX(XТX)–1XТy и yТy–
ТXТy=yТX(XТX)–1XТy и yТy– ТXТy=yТ[I–X(XТX)–1XТ]у.
ТXТy=yТ[I–X(XТX)–1XТ]у.
2. Пусть H=X(XТX)–1XТ. Покажите, что H и I–H идемпотентные и соответственно рангов р и п–р.
3. Покажите, что yТHy/s2 имеет распределение c2(р, l1), где l1=bТXТXb/(2s2), и что yТ(I–H)у/s2 имеет распределение c2(п–р).
4. Покажите, что yТHy и yТ(I–H)у независимы.
5. Покажите, что  =
= имеет распределение F(р, п–р, l1).
имеет распределение F(р, п–р, l1).
9.4. Покажите, что HH1=H1 и H1H=H1, как и в (9.2.9), где Н и H1 являются такими, как определено в (9.2.5) и (9.2.6).
9.5. Покажите, что первое и второе условия следствия 1 теоремы 5.6.3 удовлетворяются для квадратичных форм выражения (9.2.6), как отмечено в доказательстве теоремы 9.2.2.
9.6. Найдите ожидаемое среднее квадратичное числителя данной в примере 9.2.2 выражением (9.2.14) статистики FН.
9.7. В доказательстве теоремы 9.2.4 покажите, что ( ТX1Т+
ТX1Т+ ТX2Т)(X1Т
ТX2Т)(X1Т +X2
+X2 ) –(
) –( Т+
Т+ ТАТ)X1ТX1(
ТАТ)X1ТX1( +А
+А )=
)= Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2]
Т[X2ТX2–X2ТX1(X1ТX1)–1X1ТX2]  .
.
9.8. Покажите, что числитель  ТXТy–
ТXТy– ТX1Тy выражения (9.3.3) равен
ТX1Тy выражения (9.3.3) равен  /gjj в (9.3.5) (для j=р–1), как указано после (9.3.5).
/gjj в (9.3.5) (для j=р–1), как указано после (9.3.5).
Информация в лекции "Испарение" поможет Вам.
9.9. Получите доверительный интервал для aTb в (9.5.4) по статистике tL в (9.5.3).
9.10. Покажите, что tу= в (9.5.9) имеет распределение t(п–р).
в (9.5.9) имеет распределение t(п–р).
9.11. 1. Учитывая, что  =
= y0i/q представляет собой среднее q будущих наблюдений при х0, покажите, что 100(1–α)% интервал предсказания для
y0i/q представляет собой среднее q будущих наблюдений при х0, покажите, что 100(1–α)% интервал предсказания для  задается в виде
задается в виде
х0с ±s
±s tα/2(п–р).
tα/2(п–р).
2. Покажите, что для простой линейной регрессии интервал предсказания  в пункте 1 сводится к виду
в пункте 1 сводится к виду  +
+ x0±s
x0±s tα/2(п–2).
tα/2(п–2).
9.12. Получите доверительный интервал для s2 в (9.5.12) из вероятностного высказывания (9.5.11).






















