Полезные исходные множества результатов и их распределения
Глава 10 Сравнение двух объектов на основе эксперимента
Всё познаётся в сравнении, поэтому в данной главе обсуждается проблема сравнения двух объектов на основе постановки эксперимента и выяснения являются ли обнаруженные между ними различия подлинными или результат случайной вариации. Это порождает важные вопросы, связанные с выбором используемых для сравнения множеств результатов наблюдений и их распределений, а также о применении рандомизации, о размещении по блокам и о графических проверках.
10.1. Полезные исходные множества результатов и их распределения
Рассмотренный в предыдущей главе метод статистического вывода, названный проверкой значимости или проверкой гипотез, пригоден на практике для сравнения объектов одинакового назначения. Положим, рассматривается отдельный результат, полученный после изменения исследуемого объекта, сделанного, например, по рационализаторскому предложению. Необходимо установить, что этот результат является всего лишь случайной вариацией результатов работы объекта без изменения или это особый результат, подтверждающий эффективность сделанного изменения. Для решения этого вопроса необходимо сначала получить подходящее для сравнения множество результатов работы объекта до изменения. Это множество имеет своё распределение и с ним может быть сопоставлен результат, полученный после изменения. Если этот результат особый, то его называют статистически значимым. Так может осуществляться обоснованная проверка значимости результата функционирования объекта после его изменения.
В общем, под обоснованной проверкой значимости подразумевается возможность сопоставления наблюдаемого результата с пригодным для сравнения множеством возможных результатов. Если такое множество результатов непригодно для сравнения, то проверка значимости недействительна.
В рассматриваемом далее примере устанавливается ценность сделанной модификации производственного процесса на химическом заводе [Box с соавт. (2005) стр.68]. Применённые в нём подходы не ограничены рассматриваемым химическим производством и могут использоваться в других областях исследований.
Является ли изменённый метод лучше стандартного?
На химическом заводе проведён эксперимент по изготовлению одной за другой 10 партий химического вещества по стандартному методу А производства, а затем изготовлены также одна за другой 10 партий по изменённому методу В. Результаты эксперимента в виде выхода требуемого химического вещества представлены в таблице 10.1.1. Доказывают ли полученные данные, что по методу В получается больший выход требуемого вещества, чем по методу А?
Для получения ответа будет правильно начать с графического изображения данных на Рис.10.1.1 и расчёта усреднённых результатов, полученных методами А и В. Было найдено, что их усреднённые  =84,24 и
=84,24 и  =85,54 (черта над у означает арифметическое среднее). Следовательно, изменённый метод В дал усреднённое на 1,3 большее. Это изменение небольшое, но в реальном производстве может дать значительные сбережения. Однако, из-за значительной вариации выхода вещества от партии к партии, было сомнение в обоснованности утверждения, что изменённый метод В производства лучше, так как наблюдаемая разница усреднённых могла быть просто случайным событием.
=85,54 (черта над у означает арифметическое среднее). Следовательно, изменённый метод В дал усреднённое на 1,3 большее. Это изменение небольшое, но в реальном производстве может дать значительные сбережения. Однако, из-за значительной вариации выхода вещества от партии к партии, было сомнение в обоснованности утверждения, что изменённый метод В производства лучше, так как наблюдаемая разница усреднённых могла быть просто случайным событием.
Рекомендуемые материалы
Таблица 10.1.1. Данные выхода вещества в производственном эксперименте
| Номер парти | Метод | Выход | Метод | Выход |
| 1 | А | 89,7 | В | 84,7 |
| 2 | А | 81,4 | В | 86,1 |
| 3 | А | 84,5 | В | 83,2 |
| 4 | А | 84,8 | В | 91,9 |
| 5 | А | 87,3 | В | 86,3 |
| 6 | А | 79,7 | В | 79,3 |
| 7 | А | 85,1 | В | 82,6 |
| 8 | А | 81,7 | В | 89,1 |
| 9 | А | 83,7 | В | 83,7 |
| 10 | А | 84,5 | В | 88,5 |
|
|
| |||
|
|
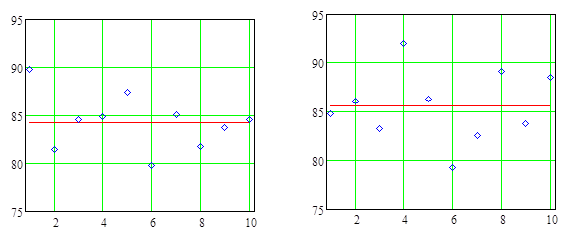
Рис. 10.1.1. Значения выхода вещества, построенные в порядке получения в партиях соответственно методами А и В.
Для решения этого вопроса были приняты во внимание результаты выхода вещества, полученные методом А в предыдущих 210 партиях. Эти данные представлены в таблице [Box с соавт. (2005) стр.120] и изображены на Рис.10.1.2. Множество 210 значений выхода вещества использовалось для определения того, как часто в прошлом случались разности между усреднёнными значениями в следующих один за другим наборах из 10 результатов не меньше 1,3. Если такие разности получаются часто, то надо сделать вывод, что разность 1,3 может быть объяснена обычной случайной вариацией результатов производственного процесса по методу А. Но, если такие разности получаются редко, то более разумным объяснением является то, что изменённый метод В производства действительно даёт реальное увеличение среднего выхода вещества.
Значения 191 разности усреднённых, следующих один за другим двух наборов из 10 результатов, представлены в таблице [Box с соавт. (2005) стр.122] и их гистограмма изображена на Рис.10.1.3. Считается, что они дают пригодное для сравнения множество разностей, с которым можно сравнить полученную разность 1,3. Однако, как обсуждалось в разделе 1.8, полученные описанным способом разности могут быть коррелированы и не имеют одинаковые вероятности быть полученными. Поэтому для того, чтобы множество разностей действительно было пригодным для сравнения надо хотя бы предположить, что эти разности получены на основе случайного выбора из 210 значений смежных наборов по 10 результатов.
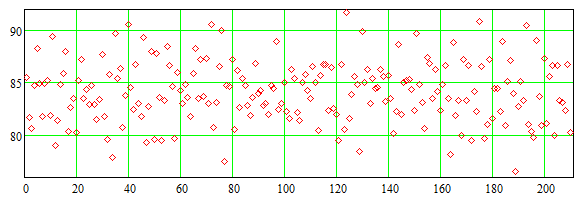
Рис.10.1.2. График 210 результатов выхода вещества в производстве методом А.
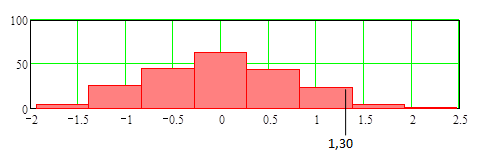
Рис.10.1.3. Гистограмма распределения 191 разности между усреднёнными значениями смежных 10 результатов по методу А.
Из гистограммы и полученных значений разностей видно, что скорее редко, то есть, только девять раз разности из множества для сравнения действительно превосходят полученную в производственном эксперименте разность +1,3. Нулевая гипотеза, что разность +1,3 является членом множества разностей для сравнения, ложна. В статистике это означает, что по отношению к множеству разностей для сравнения наблюдаемая разность была статистически значима при уровне вероятности 9/191=0,047 или на уровне значимости в 4,7%.
Эта проверка значимости, использующая внешнее распределение для сравнения, привлекательна тем, что для неё необходимы очень малые допущения. В частности, она не предполагает, что исходные данные нормально распределены или независимы и, особенно, что они не автокоррелированы. Она предполагает только, что при каких бы условиях не совершались предыдущие наблюдения, эти же условия оказывают влияние и на данные проводимого эксперимента. Однако для сравнения с использованием внешнего распределения необходимо иметь достаточно большое множество предыдущих данных, которые обоснованно могли бы рассматриваться как результат действия типичного стандартного процесса.
При поиске пригодного для сравнения множества результатов важно чтобы оно не содержало одно или более непригодных подмножеств результатов. Допустим, что после более тщательного изучения предыдущих 210 результатов производственного эксперимента, было обнаружено, что первые 50 результатов были получены, когда процесс выполнялся с использованием другого исходного сырья. Поэтому они составляют непригодное для сравнения подмножество результатов, которое должно быть исключено из пригодного для сравнения множества результатов.
Упражнение 10.1.1. Положим, что производственная ситуация была такой-же как описано выше, но получены только 10 результатов. Первые 5 методом А (89,7; 81,4; 84,5; 84,8; 87,3) и следующие 5 методом В (80,7; 86,1; 82,7; 84,7: 85,5). По данным таблицы [Box с соавт. (2005) стр.120] создайте подходящее распределение для сравнения и определите для этой проверки уровень значимости, связанный с разностью  –
– .
.
Ответ: 0,082.
Упражнение 10.1.2. Рассмотрим испытания, предназначенные для сравнения скорости роста клеток с использованием стандартного метода (А) приготовления биологических образцов и нового метода (В). Положим, четыре опыта проводились в следующие один за другим дни в последовательности А, А, В, В с результатами 23, 28, 37, 33, а перед этим последовательность опытов по методу А в следующие один за другим дни дала результаты 25, 23, 27, 31, 32, 35, 40, 38, 38, 33, 27, 21, 19, 24, 17, 15, 14, 19, 23, 22. Используя внешнее распределение для сравнения, вычислите уровень значимости для нулевой гипотезы  =
= , когда альтернативной гипотезой является
, когда альтернативной гипотезой является  >
> . Очевидно ли, что метод В даёт более высокую скорость, чем А?
. Очевидно ли, что метод В даёт более высокую скорость, чем А?
Ответ: Наблюдаемый уровень значимости 0/17=0. Очевидно, что метод В даёт более высокую скорость роста.
Случайные выборки из двух популяций
Обычно полагается, что набор данных, например, 10 результатов производственного эксперимента по методу А могут рассматриваться в виде случайной выборки из всей популяции полученных этим методом результатов. Для изображения предполагаемого вообразим, что десятки тысяч результатов выхода вещества, полученных стандартным методом А производства, записаны на билетах и помещены в большой лотерейный барабан, что схематично показано на Рис.10.1.4. Распределение вероятности этой очень большой популяции результатов представлено графиком функции плотности вероятности в нижней части того же рисунка. При справедливости гипотезы случайного выбора, 10 результатов по методу А представляются как 10 независимых случайных извлечений из лотерейного барабана А и, следовательно, из распределения А. Таким же образом результаты при изменённом методе В представляются как 10 независимых случайных извлечений из лотерейного барабана В и, следовательно, из распределения В.
Нулевой гипотезой, которую необходимо проверить, является то, что изменение метода производства не даёт никакого эффекта. Если эта гипотеза верна, то весь набор из 20 результатов по методам А и В может быть представлен в виде случайной выборки из одной общей популяции результатов. Альтернативной гипотезой является то, что распределения, из которых две случайные выборки извлечены, хотя и похожи, но имеют разные средние yA и yB. (Надо заметить, что распределения А и В не являются обязательно нормальными.)
Почему хорошо, если можно считать верной гипотезу случайного выбора? Верность допущения, что данные могут быть представлены в виде случайных выборок, значит, что переменные у1, у2,..., у10 и у11, у12,..., у20 распределены независимо около соответствующих их средних yA и yВ. Отсюда ошибки у1–yA, у2–yA, ..., у10–yA, у11–yВ, у12–yВ, ..., у20–yВ переменных у1, у2,..., у10,..., у20 полагается, что изменяются независимо одна от другой и, в частности, порядок в котором проводятся опыты не имеет влияния на результаты.
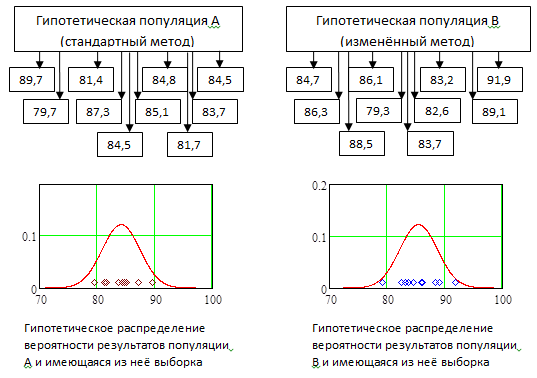
Рис.10.1.4. Случайный выбор из двух гипотетических популяций
Основанное на гипотезе случайного выбора распределение для сравнения
Положим, что в примере производственного эксперимента для сравнения не было внешнего множества результатов по методу А и единственно доступными данными были приведённые в таблице 10.1.1 два набора по 10 результатов выхода вещества, полученные методами А и В. Допустим, что они являлись случайными выборками из популяций с распределениями приблизительно одинаковой формы (и, в частности, с одинаковой дисперсией s2), но, возможно, с разными средними yA и yB. Тогда могут быть выполнены следующие вычисления.
Если данные являются случайными выборками, включающими nА=10 наблюдений из первой популяции и nВ=10 наблюдений из второй популяции, то, в силу (1.9.4), дисперсии вычисленных усреднённых находятся из выражений
D( ) =s2/nА и D(
) =s2/nА и D( ) =s2/nВ.
) =s2/nВ.
В этом случае усреднённые  и
и  распределены независимо, так что дисперсия их разности
распределены независимо, так что дисперсия их разности
D( –
– ) =s2/nА+s2/nВ =s2(1/nА+1/nВ).
) =s2/nА+s2/nВ =s2(1/nА+1/nВ).
Отсюда стандартное отклонение распределения разностей усреднённых получается
 =s
=s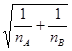
Напомним, что корень квадратный из дисперсии некоторой статистики часто называется стандартной ошибкой этой статистики.
Даже если распределения исходных наблюдений были бы умеренно отличными от нормальных, распределение разностей  –
– между усреднёнными выборок с числами членов nА=nВ=10 ожидалось бы близким к нормальному из-за центрального предельного эффекта. А если считать гипотезу случайного выбора верной и обозначить истинную разность средних популяций d =yВ–yА, то выражение
между усреднёнными выборок с числами членов nА=nВ=10 ожидалось бы близким к нормальному из-за центрального предельного эффекта. А если считать гипотезу случайного выбора верной и обозначить истинную разность средних популяций d =yВ–yА, то выражение
zо= (10.1.1)
(10.1.1)
представляет распределённое приблизительно нормально отклонение разностей  –
– усреднённых от разности d средних.
усреднённых от разности d средних.
Теперь допустим, что сведения о дисперсии s2 имеются только из nА=10 результатов по методу А и из nВ=10 результатов по методу В. Результаты оценки дисперсий по этим выборкам, в силу (1.4.3), следующие
sА2= =75,784/9=8,42 и sВ2=
=75,784/9=8,42 и sВ2= =119,924/9=13,32.
=119,924/9=13,32.
При допущении, что для результатов по методам А и В дисперсии популяций равны, то при адекватной аппроксимации оценки sА2 и sВ2 могут быть объединены для получения объединенной оценки s2 общей дисперсии s2. Это выполняется посредством сложения сумм квадратов ошибок и делением на сумму степеней свободы, как показано ниже,
s2= = (75,784+119,924)/18 =10,87.
= (75,784+119,924)/18 =10,87.
При справедливости допущения случайного выбора из популяции с нормальным распределением статистика s2 даёт оценку дисперсии s2 с nА+nВ–2=18 степенями свободы, распределённую независимо от разности  –
– . Подставляя в выражение (10.1.1) результат s оценки вместо неизвестного s, получаем выражение для статистики
. Подставляя в выражение (10.1.1) результат s оценки вместо неизвестного s, получаем выражение для статистики
tр= , (10.1.2)
, (10.1.2)
где разность ( –
– )–δ сравнивается с результатом оценки стандартной ошибки разности
)–δ сравнивается с результатом оценки стандартной ошибки разности  –
– . Тогда, на основе приведённых выше допущений и в силу (1.10.1), статистика tр имеет распределение t с nА+nВ–2=18 степенями свободы.
. Тогда, на основе приведённых выше допущений и в силу (1.10.1), статистика tр имеет распределение t с nА+nВ–2=18 степенями свободы.
В рассматриваемом примере разность  –
– =1,30 и результат оценки её стандартной ошибки
=1,30 и результат оценки её стандартной ошибки  =1,47. Для этих значений уровень вероятности, связанный с любой гипотетической разностью δ0 средних, получается на основе вычисления имеющей распределение t(18) статистики tр по формуле
=1,47. Для этих значений уровень вероятности, связанный с любой гипотетической разностью δ0 средних, получается на основе вычисления имеющей распределение t(18) статистики tр по формуле
tр0= (1,30–δ0)/1,47.
В частности (см. таблицу 10.1.2), для нулевой гипотезы H0: δ0=0 статистика tр0=1,30/1,47=0,88. Уровень вероятности Pr(tр>0,88) для этого значения статистики можно взять из таблицы значений вероятности распределения t или найти по формуле
Pr(tр>0,88)=1–pt(0.88, 18) =0,195,
где функция pt(0.88, 18) компьютерной программы Mathcad используется для вычисления интегральной вероятности до значения 0,88 для распределения t(18), как показано на Рис.10.1.5. Найденное здесь значение 0,195 сильно отличается от 0,047, полученного на основе использования внешнего распределения для сравнения. Почему? Это можно выяснить, сопоставляя внешнее и внутреннее распределения для сравнения.
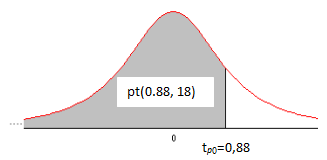
Рис. 10.1.5. Графическое изображение интегральной вероятности для распределения t
Таблица 10.1.2. Вычисление уровня значимости на основе гипотезы случайного выбора
| Метод А | Метод В | nА=10 | nВ=10 |
| 89,7 | 84,7 | Сумма SА=842,4 | Сумма SВ=855,4 |
| 81,4 | 86,1 | Усреднённое | Усреднённое |
| 84,5 | 83,2 | Разность | |
| 84,8 | 91,9 |
|
|
| 87,3 | 86,3 | ||
| 79,7 | 79,3 | ||
| 85,1 | 82,6 | ||
| 81,7 | 89,1 | ||
| 83,7 | 83,7 | ||
| 84,5 | 88,5 | ||
| Объединенная оценка общей дисперсии s2: s2=(75,784+119,924)/18 =10,8727 с v=18 степенями свободы | |||
| Оценка дисперсии разностей | |||
| Оценка стандартной ошибки разностей | |||
| tр0= | |||
| Для δ0=0 имеем tр0=1,30/1,47=0,88 с v=18 степенями свободы | |||
| Pr(tр≥0,88) =0,195. |
Упражнение 10.1.3. Удалите полученные методом В последние два результата (т.е., 83,7 и 88,5) и снова, считая гипотезу случайного выбора верной, проверьте гипотезу yВ–yА=0.
Ответ: Объединенная оценка s2=2,5791 с 16 степенями свободы, tр0=1,16/1,47=0,78, Pr(tр≥0,78) =0,228.
Сопоставление внешнего и внутреннего распределений для сравнений
На Рис.10.1.3 показана гистограмма распределения, полученная на основе внешнего множества из 210 последовательно полученных результатов. Из рисунка видно, что для этого множества результатов Pr[( –
– )≥1,30]=0,047 и полученная в эксперименте разность
)≥1,30]=0,047 и полученная в эксперименте разность  –
– =1,30 имеет уровень вероятности 0,047. Поэтому нулевую гипотезу нужно считать ложной и имеем yВ>yА.
=1,30 имеет уровень вероятности 0,047. Поэтому нулевую гипотезу нужно считать ложной и имеем yВ>yА.
Однако на Рис.10.1.6 (а) показано используемое для сравнения распределение t(18), основанное только на внутренних данных, представленных в таблице 10.1.1 и содержащих nА+nВ=20 результатов эксперимента. Для этого распределения считается, что данные получены случайным образом. В этом случае разность усреднённых  –
– =1,30 имеет вероятность 0,195 значимости, что не опровергает нулевую гипотезу yВ–yА=0.
=1,30 имеет вероятность 0,195 значимости, что не опровергает нулевую гипотезу yВ–yА=0.
Почему с использованием этих двух методов анализа получается большое расхождение в значениях вероятности значимости? Скорее всего, это вызвано корреляцией внутри ряда (автокорреляцией) расположенных рядом наблюдений. Физический смысл в данном случае был следующим. В рассматриваемом процессе выход определялся объёмом жидкого вещества в каждой следующей одна за другой партиях, но, при каждом измерении выхода, какое то количество вещества оставалось в трубах и насосах из-за особенностей конструкции системы. Следовательно, если вещество в отдельный день выкачивалось с несколько меньшей интенсивностью, то измеренный выход был меньше, но на следующий день он стремился быть больше, так как к количеству изготовляемого в этот день вещества добавлялось некоторое количество предыдущего дня. Такой эффект даёт отрицательную корреляцию между следующими один за другим выходами, как в данном примере. Более часто между следующими одно за другим значениями выхода возникает положительная автокорреляция и может дать много большие различия.
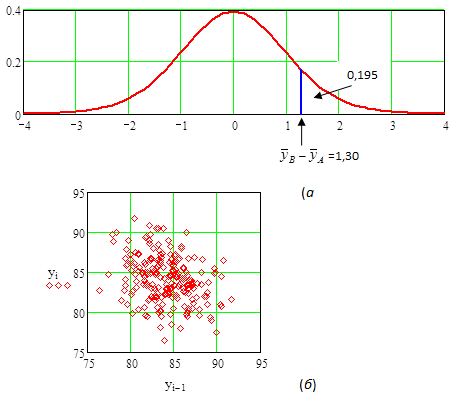
Рис.10.1.6. (a) Основанное на допущении случайного выбора внутренних данных распределение t для сравнения, (б) График зависимости уt+1 от уt для 210 результатов, показывющий оцениваемую корреляцию (автокорреляция при отставании)  =–0,289.
=–0,289.
Если гипотеза случайного выбора верна и ошибки не коррелированы, то можно использовать распределение t для сравнения. В этом случае дисперсия усреднённого находится по формуле D( )=s2/n, но для автокоррелированных данных в разделе 1.9 показано, что дисперсия D(
)=s2/n, но для автокоррелированных данных в разделе 1.9 показано, что дисперсия D( ) может быть очень отличной от этой. В частности, для последовательности наблюдений с единичной автокорреляцией r1 при отставании 1 (то есть, где каждое наблюдение коррелировано с его ближайшим соседом) показано, что дисперсия D(
) может быть очень отличной от этой. В частности, для последовательности наблюдений с единичной автокорреляцией r1 при отставании 1 (то есть, где каждое наблюдение коррелировано с его ближайшим соседом) показано, что дисперсия D( ) не равна s2/n, а является произведением Сs2/n, где С=1+2(n–1)r1/n.
) не равна s2/n, а является произведением Сs2/n, где С=1+2(n–1)r1/n.
Для полученных одно за другим 210 результатов, являющихся временным рядом и на основе которых найдено внешнее распределение для сравнения, оценка коэффициента автокорреляции при отставании 1, в силу (1.8.5), находится по формуле
 =
= =–0,289.
=–0,289.
Расчёт по формуле (1.9.6) для усреднённых n=10 результатов даёт приблизительное значение  =1+2(n–1)
=1+2(n–1) /n=0,48. В силу (1.9.5), негативная автокорреляция этих усреднённых вызывает уменьшение стандартного отклонения умножением на коэффициент
/n=0,48. В силу (1.9.5), негативная автокорреляция этих усреднённых вызывает уменьшение стандартного отклонения умножением на коэффициент  ≈0,7. Следовательно, полученное на основе предшествующих данных распределение для сравнения на Рис.10.1.3 имеет меньший разброс, чем соответствующее распределение t на Рис.10.1.6 (а). Поэтому в данном случае проверка с использованием распределения t даёт неверный ответ, так как предполагает, что ошибки распределены независимо и в результате получается распределение непригодное для сравнения.
≈0,7. Следовательно, полученное на основе предшествующих данных распределение для сравнения на Рис.10.1.3 имеет меньший разброс, чем соответствующее распределение t на Рис.10.1.6 (а). Поэтому в данном случае проверка с использованием распределения t даёт неверный ответ, так как предполагает, что ошибки распределены независимо и в результате получается распределение непригодное для сравнения.
Дисперсия распределения t находится по формуле st2=v/(v–2). Следовательно, для рассматриваемого примера, умножив её на  , получаем искомую дисперсию s2=
, получаем искомую дисперсию s2= v/(v–2) =0,54 представленного на Рис.10.1.3 распределения. Оно может быть аппроксимировано нормированным нормальным распределением с этой дисперсией и нулевым средним. Нормирование осуществляется умножением на коэффициент K=Nh, где N =191 – число разностей и h находится по формуле h=[max(
v/(v–2) =0,54 представленного на Рис.10.1.3 распределения. Оно может быть аппроксимировано нормированным нормальным распределением с этой дисперсией и нулевым средним. Нормирование осуществляется умножением на коэффициент K=Nh, где N =191 – число разностей и h находится по формуле h=[max( –
– )–min(
)–min( –
– )]/nф, где nф – число фрагментов гистограммы определяемое, например, по формуле (1.2.1). На Рис.10.1.7 показаны график нормированного нормального распределения вместе с гистограммой, полученного экспериментально распределения.
)]/nф, где nф – число фрагментов гистограммы определяемое, например, по формуле (1.2.1). На Рис.10.1.7 показаны график нормированного нормального распределения вместе с гистограммой, полученного экспериментально распределения.
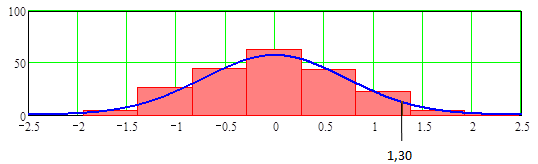
Рис.10.1.7. Нормированное нормальное распределение и гистограмма экспериментального распределения.
При такой аппроксимации уровень вероятности Pr( –
– >1,30) для значения разности
>1,30) для значения разности  –
– =1,30 можно найти по формуле
=1,30 можно найти по формуле
Pr( –
– >1,30)=1–pnorm(1,3, 0, 0,735) =0,038,
>1,30)=1–pnorm(1,3, 0, 0,735) =0,038,
где s= =0,735 и функция pnorm(1,3, 0, 0,735) компьютерной программы Mathcad используется для вычисления интегральной вероятности до значения 1,3 для нормального распределения, как показано на Рис.10.1.8. Найденное значение 0,038 несильно отличается от 0,047, полученного на основе использования внешнего распределения для сравнения.
=0,735 и функция pnorm(1,3, 0, 0,735) компьютерной программы Mathcad используется для вычисления интегральной вероятности до значения 1,3 для нормального распределения, как показано на Рис.10.1.8. Найденное значение 0,038 несильно отличается от 0,047, полученного на основе использования внешнего распределения для сравнения.
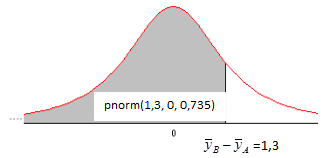
Рис. 10.1.8. Изображение интегральной вероятности до значения 1,3 затемнённой областью
Таким образом, в результате сопоставления внешнего и внутреннего распределений для сравнения получается затруднительное положение. В большинстве случаев не бывает предшествующих данных, на основе которых можно создать внешнее распределение для сравнения, а из-за влияния корреляции внутри ряда данных основанная на допущении нормального, одинакового и независимого распределения проверка с использованием распределения t неприменима. Однако постановкой рандомизированного эксперимента это затруднение может быть преодолено посредством использования рандомизированного плана для получения пригодного для сравнения набора данных [Fisher (1935)].
Рандомизированный план для экспериментального сравнения
Рассмотрим пример сравнения удобрений помидор на основе проведения эксперимента [Box с соавт. (2005) стр. 78]. Данные эксперимента получались с целью обнаружить, не влияет ли изменение смеси удобрений помидор на увеличение их урожайности. В одну грядку были посажены 11 помидор. Пять удобрялись стандартной смесью А удобрений, а остальные 6 удобрялись изменённой смесью В. Помидоры в грядке удобрялись смесями А или В в случайном порядке согласно показанному в таблице 10.1.3 плану эксперимента. Такой случайный порядок может быть получен с помощью 11 игральных карт, из которых 5 помечены А и 6 помечены В. После их тщательного перемешивания можно получить показанную в таблице случайную последовательность букв А и В. Первое растение удобрялось смесью А, как и второе, а третье удобрялось смесью В и так далее.
Таблица 10.1.3. Результаты рандомизированного эксперимента (урожаи помидор)
| Помидоры | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Удобрения | А | А | В | В | А | В | В | В | А | А | В | |
| Урожаи | 29,9 | 11,4 | 26,6 | 23,7 | 25,3 | 28,5 | 14,2 | 17,9 | 16,5 | 21,1 | 24,3 | |
| Удобрение А | 29,9 | 11,4 | 25,3 | 16,5 | 21,1 | nA=5, |
| |||||
| Удобрение В | 26,6 | 23,7 | 28,5 | 14,2 | 17,9 | 24,3 | nB=6, | |||||
Считается, что используемая в этом эксперименте физическая рандомизация делает возможным проводить обоснованные проверки значимости вводимого изменения без всяких других допущений о форме распределения [Fisher (1935) стр. 21]. Для данного примера этому приводится следующее объяснение [Box с соавт. (2005) стр. 78].
Действительно, использованный в таблице 10.1.3 план проведения эксперимента с применением смесей А и В удобрений является одним из  =
= =462 возможных комбинаций применения 5 смесей А и 6 смесей В в 11 опытах и любая комбинация применения смесей может быть выбрана с одинаковой вероятностью. Таким образом, считая верной гипотезу, что изменение смеси удобрений не влияет на урожаи помидор, можно найти пригодное для сравнения множество из 462 разностей усреднённых, получаемых при 462 комбинациях применения смесей А и В для одних и тех же значений урожаев таблицы 10.1.3. В этом случае множество для сравнения получается не в результате постановки 462 экспериментов, а в результате расчёта получаемых при 462 комбинациях применения смесей А и В разностей усреднённых.
=462 возможных комбинаций применения 5 смесей А и 6 смесей В в 11 опытах и любая комбинация применения смесей может быть выбрана с одинаковой вероятностью. Таким образом, считая верной гипотезу, что изменение смеси удобрений не влияет на урожаи помидор, можно найти пригодное для сравнения множество из 462 разностей усреднённых, получаемых при 462 комбинациях применения смесей А и В для одних и тех же значений урожаев таблицы 10.1.3. В этом случае множество для сравнения получается не в результате постановки 462 экспериментов, а в результате расчёта получаемых при 462 комбинациях применения смесей А и В разностей усреднённых.
В приложении этой главы показано как может быть найдено множество из 462 разностей усреднённых на современных компьютерах. Гистограмма этих разностей усреднённых показана на Рис.10.1.9 вместе с полученной в эксперименте разностью  –
– =1,69 из таблицы 10.1.3. Так как 154 из возможных 462 комбинаций смесей А и В дают разности больше 1,69, то уровень вероятности получается 154/462=0,333. Поэтому нет смысла сомневаться в правильности нулевой гипотезы, что одна смесь удобрений имеет такое же влияние на урожаи, как и другая.
=1,69 из таблицы 10.1.3. Так как 154 из возможных 462 комбинаций смесей А и В дают разности больше 1,69, то уровень вероятности получается 154/462=0,333. Поэтому нет смысла сомневаться в правильности нулевой гипотезы, что одна смесь удобрений имеет такое же влияние на урожаи, как и другая.
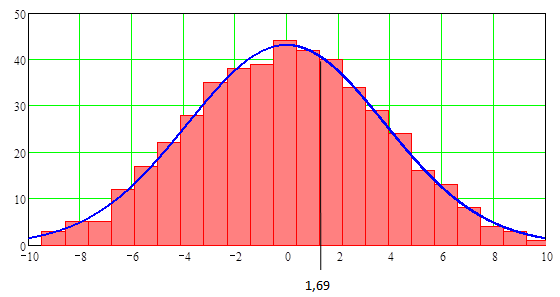
Рис.10.1.9. Гистограмма разностей усреднённых, полученных в результате рассмотрения 462 комбинаций смесей А и В, и график функции плотности вероятности нормированного нормального распределения
Сравнение с использованием распределения t
Допуская нормальное, независимое и одинаковое распределение при случайном выборе из популяции с нормальным распределением и обозначая разность между средними δ=yB–yA, в силу (1.10.1), статистика  имеет распределение t с n=nВ+nА–2 степенями свободы (см. таблицу 10.1.4 для пояснения). Для рассматриваемого примера разность
имеет распределение t с n=nВ+nА–2 степенями свободы (см. таблицу 10.1.4 для пояснения). Для рассматриваемого примера разность  –
– =1,69. Поэтому нулевая гипотеза δ =0 может быть проверена путём вычисления статистики tр0= (1,69–0)/3,82=0,44. Уровень вероятности Pr(tр>0,44) для этого значения статистики можно взять из таблицы значений вероятности распределения t(9) или, как ранее, найти по формуле
=1,69. Поэтому нулевая гипотеза δ =0 может быть проверена путём вычисления статистики tр0= (1,69–0)/3,82=0,44. Уровень вероятности Pr(tр>0,44) для этого значения статистики можно взять из таблицы значений вероятности распределения t(9) или, как ранее, найти по формуле
Pr(tр>0,44)=1–pt(0.44, 9) =0,335,
используя компьютерную программу Mathcad. Это значение уровня вероятности сравнимо со значением 0,333, полученным в результате проверки с использованием множества из 462 разностей усреднённых, найденных при 462 комбинациях применения смесей А и В.
Таким образом, в этом примере результат, полученный на основе допущения нормального, независимого и одинакового распределения, очень близок к тому, который найден с использованием множества из 462 разностей усреднённых. График функции плотности вероятности нормированного нормального распределения с результатом оценки стандартной ошибки разностей  –
– равной 3,82 показан также на Рис.10.1.9. Кроме этого заметим, что проверка на основе рандоминизированного эксперимента освобождает от соблюдения допущений независимости ошибок и нормального распределения [Box с соавт. (2005) стр.80]. Во время изобретения этой проверки вычисления делались медленно, но на современных компьютерах вычисление рандомизированного распределения даёт практический метод для проверки значимости и для вычисления доверительных интервалов.
равной 3,82 показан также на Рис.10.1.9. Кроме этого заметим, что проверка на основе рандоминизированного эксперимента освобождает от соблюдения допущений независимости ошибок и нормального распределения [Box с соавт. (2005) стр.80]. Во время изобретения этой проверки вычисления делались медленно, но на современных компьютерах вычисление рандомизированного распределения даёт практический метод для проверки значимости и для вычисления доверительных интервалов.
Таблица 10.1.4. Вычисление уровня вероятности Pr(tр≥δ0) для эксперимента с удобрениями помидор
|
|
| sА2= |
| sВ2= |
| Объединенная оценка общей дисперсии s2: s2=(SA+SB)/(vA+vB)=(vAsА2+vBsВ2)/(vA+vB)=(4x52,50+5x29,51)/(4+5)=39,73 c n=nВ+nА–2=nA+nB=9 степенями свободы |
| Оценка дисперсии разности |
| Оценка стандартной ошибки разностей |
| tр0= где δ0 гипотетическое значение δ |
| Если δ0=0, то tр0=0,44 с v=9 степенями свободы |
| Pr(tр ≥ δ0) =Pr(tр ≥0,44) =0,335 |
Упражнение 10.1.4. Создайте распределение для сравнения путём перебора вариантов применения смесей А и В и соответствующее распределение t. Каков уровень вероятности в каждом случае для приведённых ниже данных рандомизированного эксперимента?
| А | В | В | А | В |
| 3 | 5 | 5 | 1 | 8 |
Ответ: 0,1; 0,07.
Упражнение 10.1.5. Повторите предыдущее упражнение со следующими данными:
| В | А | В | А | А | А | В | В |
| 32 | 30 | Люди также интересуются этой лекцией: Введение и содержание. 31 | 29 | 30 | 29 | 31 | 30 |



 =75,784
=75,784 =119,924
=119,924 =
= =1,47
=1,47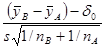
 =3,82
=3,82 =
= =
= ,
,

















