Основы метода

13.1. Основы метода

Рассмотрим некоторую зависимость отклика от двух числовых нормированных факторов, например, х₁ - давления и х₂ - температуры. На Рис.13.1.1 показан график истинной неизвестной функции у=f(х₁, х₂) зависимости отклика от двух факторов. Целью метода скорейшего улучшения отклика является нахождение таких значений факторов, при которых получаются быстро улучшающиеся значения переменных отклика. Этот метод применяют на ранней стадии исследования, когда возможно значительное улучшение отклика. В находящейся далеко от оптимума области Ξ значений факторов эксперимента по двухуровневому плану 2², показанному 4 чёрными точками, с соответствующими результатами, показанными синими точками на графике функции отклика, ожидается, что модель с полиномиальной функцией первого порядка даст хорошую аппроксимацию зависимости переменных отклика от факторов. Показанное синими стрелками на графике функции отклика направление в сторону увеличения отклика является направлением скорейшего его улучшения. Линейная модель с полиномиальной функцией первого порядка строится на основе результатов эксперимента по плану 2² в области Ξ.

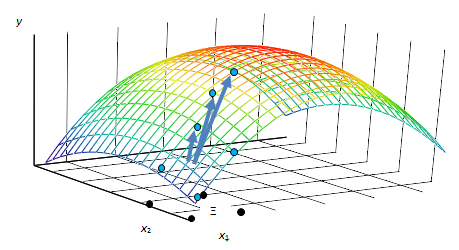
Рис.13.1.1. Графическое изображение процедуры скорейшего улучшения отклика на основе начального эксперимента по плану 2²

Показанные на Рис.13.1.1 синими кружками результаты опытов проводимых в направлении скорейшего улучшения отклика обычно демонстрируют улучшающиеся его значения. При этом полагают, что опыт с наибольшим или наименьшим значением отклика может стать центром нового плана первого порядка, на основе которого возможно дальнейшее движение в направлении скорейшего улучшения отклика [Box, Draper (2007) стр.189].

В пространстве значений факторов координаты опытов в направлении скорейшего улучшения отклика зависят от знаков и значений результатов оценки воздействий факторов. На Рис.13.1.2 показана контурная диаграмма истинной функции отклика в двумерном пространстве значений факторов. В этом пространстве можно найти координаты опыта Р – конца вектора направления скорейшего улучшения отклика.

В общем случае п-мерного пространства значений факторов начальный двухуровневый эксперимент следует выполнять по полному 2^р или дробному плану разрешающей способности не ниже IV и постулировать линейную модель у=Хβ+ε первого порядка для зависимости переменных отклика от нормированных факторов. Для случая с двумя факторами можно использовать результаты эксперимент по плану 2² с центром в точке О, имеющей координаты х₁=х₂=0. Значения нормированных факторов х₁, х₂, …, х_р получаются по формуле (2.6.4) в виде

х_j=[ξ_j–ξ_j0]/S_j,   (j =1, 2, …, р)                        (13.1.1)

где ξ_j0 =(ξ_j++ξ_j–)/2 – основной уровень, S_j =(ξ_j+–ξ_j–)/2 – интервал варьирования, а ξ_j+ и ξ_j– соответственно верхний и нижний уровни j-го фактора в натуральных единицах измерений. Результаты опытов эксперимента по показанному на Рис.13.1.2 четырьмя чёрными точками плану 2² позволяют оценить воздействия факторов на отклик и сформулировать оценочную функцию линейной модели. Координаты показанного синим кружком опыта Р являются также значениями факторов х₁ и х₂, указывая место конца вектора направления скорейшего улучшения отклика.

Рекомендуемые материалы

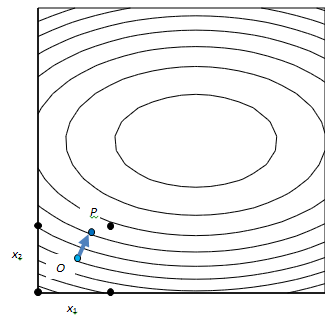
Рис.13.1.2. Направление скорейшего улучшения отклика в двумерном пространстве

Расчёт значений факторов для опытов скорейшего улучшения отклика осуществляется методом градиента [Налимов, Чернова (1965) стр.60; Адлер с соавт. (1976) стр.209; Спиридонов (1981) стр.32; Грачёв, Плаксин (2005) стр.79; Myers с соавт. (2016) стр.237]. По этому методу находится градиент функции φ отклика в виде

=i+j+…+p,                                               (13.1.2)

где i, j, …, p – единичные векторы в направлениях координатных осей. Полагается, что функция φ непрерывна, однозначна и не имеет особых точек.

Функцию отклика получают на основе линейного моделирования двухуровневого эксперимента в локальном подпространстве значений факторов. При этом постулируют обычно линейную модель у=Хβ+ε, которая для одного опыта записывается в виде

у=β₀х₀+β₁х₁+β₂х₂+…+β_рх_р+ε.                                   (13.1.3)

В ней присутствует фактор х₀ средних переменных отклика в опытах эксперимента. Полагается, что этот фактор во всех опытах эксперимента находится на уровне +1. Но это не значит, что он является постоянным. Для эксперимента с повторными опытами дисперсионная линейная модель (6.4.10) классификации по одному признаку учитывает изменения этого фактора от опыта к опыту. В модели (13.1.3) эти изменения в некоторой степени описываются членами с факторами х₁, х₂, …, х_р. Но при этом фактор х₀ остаётся переменным. Оценка параметров модели (13.1.3) методом наименьших квадратов даёт результаты , , …,  и оценочная функция отклика принимает вид

=х₀+х₁+х₂+…+х_р.                              (13.1.4)

где  - результат оценки ожидаемого значения переменной отклика. Беря градиент этой функции, получаем, что он является не (13.1.2), а

=g+i+j+…+p,                        (13.1.5)

где g - единичный вектор в направлении координатной оси х₀.

В методе градиента также считается, что частные производные в (13.1.2) являются результатами оценки параметров модели (13.1.3). Поэтому в опытах по направлению скорейшего улучшения отклика значения факторов изменяют пропорционально результатам оценки параметров модели (13.1.3), с учётом их знаков. В натуральных единицах измерений факторов, величины шагов их изменения берутся пропорционально произведениям результатов оценки параметров на соответствующие интервалы варьирования факторов. Но для использования действительного градиента (13.1.5) функции отклика необходимо изменять также и фактор х₀. Однако этот фактор является неконтролируемым и, несмотря на то, что результат  оценки его параметра обычно много больше остальных, им в расчёте методом градиента пренебрегают. Поэтому этот метод расчёта факторов для опытов скорейшего улучшения отклика нельзя считать корректным.

В другом методе расчёта факторов для опытов скорейшего улучшения отклика используется нормирование результатов оценки параметров модели (13.1.3) длиной составленного из них вектора [Box, Draper (2007) стр.191]. При этом  тоже не учитывается, и сначала находят длину вектора [, , …, ] оценки параметров по формуле =(++…+)^1/2, а затем, каждый результат оценки делят на . В результате получается вектор [, , …, ] единичной длины. Далее считается, что умножение этого вектора, например, на числа 2, 4, 6 и 8 даёт значения нормированных факторов для опытов в направлении скорейшего улучшения отклика. Перевод факторов из нормированных в натуральные единицы измерений делается по получаемой из (13.1.1) формуле

ξ_i=х_jS_j+ξ_j0.                                                      (13.1.6)

Однако и в этом случае без учёта  расчёт факторов для опытов скорейшего улучшения отклика получается некорректным.

Оценка факторов для опытов скорейшего улучшения отклика

Для оценки факторов устанавливаемых в опытах скорейшего улучшения отклика необходимо иметь функцию отклика, содержащую только контролируемые факторы. Такая функция линейной модели начального эксперимента получается в результате нормирования переменных отклика его опытов. В разделе 7.5 показано как нормируются факторы, принимающие в эксперименте многие значения. По аналогии нормирование переменных отклика выполняется по формуле

=(у_i–)/S_у,                                                (13.1.7)

где = - усреднённое их значение и S_у= - интервал варьирования. В случае начального эксперимента по плану 2² имеем п=4. В разделе 4.3 показано, что при таком нормировании переменные  остаются распределёнными нормально, если исходные переменные у_i распределены по нормальному закону. При достаточно большой выборке значений переменных  нормальность распределения можно проверить по графику кумулятивных вероятностей их распределения.

После нормирования переменных отклика постулируемая модель принимает вид

=Х+ε                                                      (13.1.8)

и её вектор  параметров оценивается методом наименьших квадратов по формуле

b=(X^TX)^–1X^T,                                            (13.1.9)

где Х – матрица модели и  - вектор нормированных переменных отклика. Вектор b отличается от вектора оценки параметров модели (13.1.3).

С использованием элементов вектора b оценки параметров модели (13.1.8) оценка ожидаемых значений нормированных переменных отклика делается по формуле

=b₁x₁+b₂x₂+...+b_рx_р,                                   (13.1.10)

так как при нормированных переменных отклика b₀=0. Это получается потому, что в матрице Х первый вектор-столбец состоит из единиц. Его произведение на вектор , в силу (13.1.7), даёт 1^Т=(–п)/S_у, а произведение 1^Т1=п. Поэтому, в силу (13.1.9), получаем b₀=1^Т/п=(–)/S_у=0.

В отличие от элементов вектора оценки параметров модели (13.1.3) элементы вектора b являются безразмерными, как и нормированные факторы. Оценочная функция (13.1.10) отклика модели (13.1.8) содержит только контролируемые факторы и пригодна для использования в методе градиента. Но статистический метод скорейшего улучшения отклика не является шаговой процедурой. Метод крутого восхождения формулировался в виде задачи на условный экстремум [Box, Wilson (1951); Налимов, Чернова (1965) стр.60]. В результате нахождения условного экстремума с использованием функции (13.1.10) можно получить оценку факторов для опытов скорейшего улучшения отклика.

В двумерном пространстве на Рис.13.1.2 для достижения условного экстремума нужно перейти из точки О в находящуюся от неё на расстоянии r точку Р, где достигается максимальное улучшение отклика. Точка О находится в начале отсчёта и, в силу (13.1.10), отклик в ней =0, а в точке Р отклик =b₁x₁+b₂x₂. Так как расстояние между О и Р равно r, то по теореме Пифагора имеем x₁²+x₂²=r². Так получается и в п-мерном пространстве значений факторов, где векторы уровней факторов ортогональны между собой. В этом случае расстояние между О и Р также равно r и получаем ограничение x₁²+x₂²+...+x_р²=r², так как вектор-столбцы полного 2^р или дробного двухуровневых планов между собой ортогональны.

При этом ограничении необходимо чтобы в направлении скорейшего улучшения отклика разность – была максимальной. Эта задача оптимизации с ограничением решается методом множителей Лагранжа. Если множитель Лагранжа обозначить l, то функция Лагранжа в данном случае принимает вид

L(x₁, x₂,..., x_р, l)=b₁x₁+b₂x₂+...+b_рx_р––l(x₁²+x₂²+...+x_р²–r²).       (13.1.11)

Пусть в пределах рассматриваемой области значений факторов частные производные этой функции по х₁, х₂,..., x_р являются непрерывными. Они получаются следующими:

¶L(x₁, x₂,..., x_р, l)/¶x₁=b₁–2lx₁,

¶L(x₁, x₂,..., x_р, l)/¶x₂=b₂–2lx₂,

...                                                                    (13.1.12)

¶L(x₁, x₂,..., x_р, l)/¶x_р=b_р–2lx_р.

Приравнивая эти производные нулю и решая полученные уравнения относительно x₁, x₂,..., x_р, получаем формулы оценки факторов

=b₁/(2l), =b₂/(2l),..., =b_р/(2l).                                (13.1.13)

По этим формулам делается оценка факторов для опыта скорейшего улучшения отклика, так как в них используются элементы вектора b оценки параметров модели (13.1.8). В этих формулах коэффициент пропорциональности а=1/(2l) и оценка координат точки Р делается по формулам

=аb₁, =аb₂,..., =аb_р.                                     (13.1.14)

А если для модели (13.1.8) соблюдаются допущения Е()=Х и С()=s²I, то по следствию теоремы Гаусса-Маркова для a^Т, где вектор а=а1, статистика a^Тb является наилучшей линейной несмещенной оценкой. Здесь выбор значения а просто определяет расстояние от центра О плана на котором должен находиться опыт Р и, считая b₁, b₂, …, b_р базисными векторами, линейная комбинация a^Тb определяет вектор направления скорейшего улучшения отклика.

Для проведения опытов в направлении скорейшего улучшения отклика необходимо иметь для них значения факторов в натуральных единицах измерений и поэтому безразмерные , ,...,  пересчитываются в натуральные единицы измерений. А так как оценка факторов x₁, x₂,..., x_р делается при ограничении x₁²+x₂²+...+x_р²=r², то, в силу (13.1.6), для этого можно использовать следующие выражения

= ξ₁₀+S₁, = ξ₂₀+S₂, ..., = ξ_р0+S_р.                  (13.1.15)

При этом необходимо также учитывать происходящее увеличение или уменьшение отклика при скорейшем его улучшении. Для показанного на Рис.13.1.1 увеличения отклика, знаки , ,...,  принимаются теми, что получены в (13.1.14), а при его уменьшении эти знаки необходимо изменить на обратные. Таким образом, в случае увеличения отклика используются формулы

=ξ₁₀+аb₁S₁, =ξ₂₀+аb₂S₂, ..., =ξ_р0+аb_рS_р,                   (13.1.16)

а в случае его уменьшения - формулы

=ξ₁₀–аb₁S₁, =ξ₂₀–аb₂S₂, ..., =ξ_р0–аb_рS_р.                   (13.1.17)

Рассмотренная процедура оценки факторов для опытов скорейшего улучшения отклика может использоваться для конкретного числа факторов, например двух, простым исключением остальных. И найденные результаты оценки факторов могут несколько отличаться от устанавливаемых значений факторов в реальных опытах скорейшего улучшения отклика, например, из-за технологических ограничений.

Однако если в этих опытах факторы устанавливаются точно с полученными по формулам (13.1.14) нормированными значениями, то подставляя их в (13.1.10) вместо x₁, x₂,..., x_р, можно предсказать оцениваемые ожидаемые значения нормированных переменных отклика в опытах скорейшего улучшения отклика по формуле

=b₁+b₂+...+b_р=аb^Tb.

Эти значения затем, в силу (13.1.7), по формуле

у_а=+S_у                                                   (13.1.18)

можно преобразовать в натуральные единицы измерений. Таким образом, на основе модели (13.1.8) можно также предсказывать значения переменных отклика в опытах скорейшего улучшения отклика. Оценить качество предсказаний можно по сумме квадратов остатков предсказания (8.6.11) или статистике R_p² предсказания (8.6.12).

Из формул (13.1.16) и (13.1.17) следует, что оценка факторов для опытов скорейшего улучшения отклика зависит от выбираемых основных уровней и интервалов варьирования факторов начального двухуровневого эксперимента. Если этот эксперимент проводить при других основных уровнях и интервалах варьирования факторов, чем эксперимент в области Ξ на Рис.13.1.1, то по его результатам получится другой результат оценки параметров модели (13.1.8). Для одной и той же истинной функции у=f(х₁, х₂) отклика на Рис.13.1.1 этот эксперимент будет располагаться в другой области Ψ. Для него направление проведения опытов скорейшего улучшения отклика и факторы в них будут отличаться от тех, что получены для эксперимента в области Ξ. Поэтому направление проведения опытов скорейшего улучшения отклика и факторы в них определяются условиями проводимого начального двухуровневого эксперимента, то есть, выбираемыми для него значениями основных уровней и интервалов варьирования факторов.

Кроме этого в разделе 2.6 было отмечено и показано на Рис.2.6.2, что при двух факторах определяемая полиномами второго порядка функция отклика может принимать формы отличные от показанного на Рис.13.1.1 простого максимума. В случаях простого максимума и поднимающегося гребня начальные двухуровневые эксперименты в разных областях Ξ и Ψ дадут разные направления скорейшего улучшения, но оба они направлены к одному абсолютному или условному максимуму. Однако в случае функции отклика в виде стационарного гребня начальные двухуровневые эксперименты в разных областях дадут направления к максимуму с разными координатами. А в случае функции отклика в виде седла или минимакса при поиске максимального значения отклика даже при постановке одного начального двухуровневого эксперимента может появиться два направления скорейшего улучшения отклика.

Выше рассмотренные варианты справедливы только для функций отклика в виде полиномов второго порядка с двумя факторами, которые можно представить графически в трёх измерениях. Однако для начальных экспериментов с тремя и большим числом факторов функции отклика в виде полиномов второго и более высокого порядка имеют более сложные геометрические формы с много большим разнообразием расположений максимумов и минимумов. В общем случае истинные неизвестные функции отклика могут представлять собой сложные нелинейные функции от любого числа факторов. Поэтому при любом числе факторов начальных экспериментов правильная оценка факторов для опытов скорейшего улучшения отклика является очень важной.

Доверительные интервалы факторов

Общую доверительную область факторов, контролируемых в опытах скорейшего улучшения отклика, можно найти для ряда увеличивающихся от нуля действительных чисел а на основе оценки факторов по формулам (13.1.16) и (13.1.17). Эти формулы в матричном виде записываются соответственно следующим образом

=ξ₀+аDb₁ и =ξ₀–аDb₁,                                       (13.1.19)

где D= и ξ₀=. В них b₁ - вектор оценки всех параметров модели (13.1.8), за исключением , оценка которого даёт b₀=0. Поэтому фактор х₀ можно исключить из модели (13.1.8) и записать её в виде

=Х₁+ε,                                                   (13.1.20)

где матрица Х₁ модели является матрицей полного 2^р или дробного двухуровневого плана разрешающей способности не ниже IV.

Формулы (13.1.19) оценки факторов для опытов скорейшего улучшения отклика получены с использованием функции (13.1.10), являющейся функцией зависимости оцениваемых ожидаемых значений нормированных переменных отклика от нормированных факторов. А если взять функцию Е()=Х₁ зависимости ожидаемых значений нормированных переменных отклика от нормированных факторов, то в форме функции (13.1.10) её можно записать в виде

Е()=x₁+x₂+...+x_р.

С использованием этой функции в двумерном пространстве на Рис.13.1.2 в задаче условного экстремума нужно перейти из точки О в находящуюся от неё на расстоянии r точку Р, где достигается максимальное улучшение отклика. Точка О находится в начале отсчёта и отклик в ней Е()=0, а в точке Р отклик Е()=x₁+x₂. Так как расстояние между О и Р равно r, то x₁²+x₂²=r². Для п-мерного пространства значений факторов, где векторы уровней факторов ортогональны между собой, расстояние между О и Р тоже равно r и имеем ограничение x₁²+x₂²+...+x_р²=r². При этом ограничении надо чтобы в направлении скорейшего улучшения отклика разность Е()–Е() была максимальной.

Для оптимизации с ограничением используем тоже метод множителей Лагранжа и, если, как и в (13.1.11), l - множитель Лагранжа, то функция Лагранжа принимает вид

L(x₁, x₂,..., x_р, l)=x₁+x₂+...+x_р–l(x₁²+x₂²+...+x_р²–r²).

В пределах рассматриваемой области значений факторов частные производные этой функции по х₁, х₂,..., x_р являются непрерывными и получаются следующими

¶L(x₁, x₂,..., x_р, l)/¶x₁=–2lx₁,

¶L(x₁, x₂,..., x_р, l)/¶x₂=–2lx₂,

...

¶L(x₁, x₂,..., x_р, l)/¶x_р=–2lx_р.

Приравнивая эти производные нулю и решая полученные уравнения относительно x₁, x₂,..., x_р, получаем выражения для нормированных факторов

x₁=/(2l), x₂=/(2l),..., x_р=/(2l).                               (13.1.21)

По ним получаются нормированные факторы для опыта скорейшего улучшения отклика, так как при этом используются параметры модели (13.1.20), а не результаты их оценки. Коэффициент пропорциональности в этом случае тоже а=1/(2l) и координаты точки Р находятся по формулам

x₁=а, x₂=а,..., x_р=а.

Выбор числа а определяет расстояние от центра О плана на котором должен находиться опыт Р в направлении скорейшего улучшения отклика.

Для преобразования безразмерных x₁, x₂,..., x_р в натуральные единицы измерений, в силу (13.1.6), можно использовать следующие выражения

ξ₁=ξ₁₀+x₁S₁, ξ₂=ξ₂₀+x₂S₂, ..., ξ_р=ξ_р0+x_рS_р.

И здесь также учитывается происходящее увеличение или уменьшение отклика при его скорейшем улучшении. Для показанного на Рис.13.1.1 увеличения отклика, знаки x₁, x₂,..., x_р принимаются теми, что получены в (13.1.21), а при уменьшении отклика эти знаки необходимо изменить на обратные. Таким образом, в случае увеличения отклика надо использовать формулы

ξ₁=ξ₁₀+аS₁, ξ₂=ξ₂₀+аS₂, ..., ξ_р=ξ_р0+аS_р,

а в случае его уменьшения - формулы

ξ₁=ξ₁₀–аS₁, ξ₂=ξ₂₀–аS₂, ..., ξ_р=ξ_р0–аS_р.

Эти формулы в матричном виде записываются так

ξ=ξ₀+аD и ξ=ξ₀–аD,                                        (13.1.22)

где ξ - вектор факторов в а-м опыте скорейшего улучшения.

Теперь, если из выражений (13.1.19) вычесть соответствующие выражения (13.1.22), то получаем

–ξ=аD(b₁–) и –ξ=–аD(b₁–),

а после их преобразований имеем

(b₁–)=D^–1(–ξ)/а и (b₁–)=–D^–1(–ξ)/а.                      (13.1.23)

Эти формулы содержат вектор b₁ оценки параметров модели (13.1.20). Если вектор  нормированных переменных отклика этой модели имеет нормальное распределение N_n(X, s²I), то, в силу (9.5.1), для элементов вектора  их 100(1–a)% совместная доверительная область состоит из всех их значений, удовлетворяющих неравенству

(b₁–)^ТX₁^ТX₁(b₁–)≤рs²F_кр,                                  (13.1.24)

где F_кр - критическое значение случайной переменной с распределением F(р, п–р) и интегральной вероятностью 1–α на интервале от 0 до F_кр, р - число факторов модели (13.1.20) и s² - результат оценки дисперсии для этой модели. Подставляя в выражение (13.1.24) вместо (b₁–) их выражения из (13.1.23), получаем

(–ξ)^ТD^–1X₁^ТX₁D^–1(–ξ)≤а²рs²F_кр.                         (13.1.25)

Для ряда увеличивающихся от нуля чисел а все значения элементов вектора ξ, удовлетворяющие неравенству (13.1.25), образуют 100(1–α)% совместную их доверительную область.

Геометрическое представление этой доверительной области в трёх измерениях возможно только для двух факторов и изменяющегося а. При числе факторов больше двух пользование выражением (13.1.25) для анализа становится затруднительным и поэтому лучше использовать доверительные интервалы для каждого фактора.

Как и при нахождении доверительной области факторов, используя функцию Е()=x₁+x₂+...+x_р в решении задачи на условный экстремум и метод множителей Лагранжа, можно получить следующие выражения для факторов в натуральных единицах измерений

ξ₁=ξ₁₀+аS₁, ξ₂=ξ₂₀+аS₂,..., ξ_р=ξ_р0+аS_р,                   (13.1.26)

ξ₁=ξ₁₀–аS₁, ξ₂=ξ₂₀–аS₂,..., ξ_р=ξ_р0–аS_р.                    (13.1.27)

Далее, вычитая выражения (13.1.26) из соответствующих выражений в (13.1.16) и выражения (13.1.27) из соответствующих выражений в (13.1.17) получаем

–ξ₁=аS₁(b₁–), –ξ₂=аS₂(b₂–),..., –ξ_р=аS_р(b_р–),

–ξ₁=–аS₁(b₁–), –ξ₂=–аS₂(b₂–),..., –ξ_р=–аS_р(b_р–),

а после их преобразований имеем

b₁–=(–ξ₁)/(аS₁), b₂–=(–ξ₂)/(аS₂),..., b_р–=(–ξ_р)/(аS_р),         (13.1.28)

b₁–=–(–ξ₁)/(аS₁), b₂–=–(–ξ₂)/(аS₂),..., b_р–=–(–ξ_р)/(аS_р).   (13.1.29)

Если s – найденное с использованием модели (13.1.20) выборочное стандартное отклонение и g_jj – j-й диагональный элемент матрицы (X₁^ТX₁)^–1, то, как показано в разделе 9.5, статистика (b_j–)/(s) имеет центральное распределение t. Полагая, что вероятность

Pr[–t_α/2(п–р)≤(b_j–)/(s)≤t_α/2(п–р)]=1–α,

и подставляя вместо (b_j–) их выражения из (13.1.28) и (13.1.29), получаем

Pr[–t_α/2(п–р)≤(–ξ_j)/(аS_js)≤t_α/2(п–р)]=1–α,

Pr[–t_α/2(п–р)≤–(–ξ_j)/(аS_js)≤t_α/2(п–р)]=1–α,

а после преобразований в квадратных скобках имеем соответственно

Pr[–аS_jst_α/2(п–р)≤ ξ_j ≤+аS_jst_α/2(п–р)]=1–α,

Pr[–аS_jst_α/2(п–р)≤ ξ_j ≤+аS_jst_α/2(п–р)]=1–α.

Следовательно, 100(1–α)% доверительный интервал для отдельного фактора ξ_j рассчитывается по формуле ±аS_jst_α/2(п–р) или, с учётом (13.1.16) и (13.1.17), соответственно по формулам

ξ_j0+аS_j[b_j±st_α/2(п–р)]                                         (13.1.30)

и

ξ_j0–аS_j[b_j±st_α/2(п–р)].                                        (13.1.31)

Эти формулы позволяют рассчитать доверительные интервалы факторов в опытах скорейшего улучшения соответственно при увеличивающихся и уменьшающихся переменных отклика.

Скорейшее улучшение отклика при ограничении

В процедуре скорейшего улучшения отклика, если значения факторов изменить на недопустимо большие величины от их основных уровней, то объект исследования может потерять работоспособность. Поэтому в общем случае для факторов существуют предельные максимальные или минимальные значения, которыми ограничивается область их изменений. Так, если в двухуровневом эксперименте j-й фактор ξ_j устанавливается на двух уровнях ξ_j0±S_j, то в опытах скорейшего улучшения отклика в зависимости от его увеличения или уменьшения этот фактор может принять максимально или минимально возможные значения ξ_j0±Sm_j, где Sm_j - максимально возможное изменение фактора от его основного уровня ξ_j0. Таким образом, в силу (13.1.26) и (13.1.27), для параметров модели (13.1.20) должны соблюдаться неравенства аS_j≤ Sm_j или –аS_j≥ –Sm_j. И если значения а, S_j и Sm_j известны, то на параметры модели (13.1.20) накладываются ограничения ≤Sm_j/(аS_j).

При таких ограничениях параметры модели (13.1.20) должны оцениваться для выбираемых значений а. Так, если первый опыт скорейшего улучшения планируется провести при а=2, то максимальные значения параметров модели (13.1.20) находятся из выражений =Sm_j/(2S_j). Это является ограничением оценки параметров модели. В векторной форме это ограничение записывается так

==t₁.                                    (13.1.32)

По теореме 9.3.6, если матрица С=I, то для модели (13.1.20) с указанным ограничением результатом оценки вектора  её параметров является вектор

b₂=b₁–(X₁^ТX₁)^–1[(X₁^ТX₁)^–1]^–1(b₁–t₁)

=t₁,                                                                 (13.1.33)

где b₁= (X₁^ТX₁)^–1X₁^Т. Таким образом, в выражениях (13.1.16) и (13.1.17) оценки факторов для первого (а=2) опыта скорейшего улучшения отклика надо использовать соответствующие элементы вектора b₂, а не вектора b₁.

Для планируемого второго опыта скорейшего улучшения при а=3 максимальные значения параметров модели (13.1.20) определяются выражениями =Sm_j/(3S_j). Они являются ограничением при оценке параметров модели для этого опыта. В векторной форме это ограничение записывается так

==t₂.                                    (13.1.34)

По теореме 9.3.6 и при С=I для модели (13.1.20) с новым ограничением результатом оценки вектора  её параметров является вектор

b₃=b₁–(X₁^ТX₁)^–1[(X₁^ТX₁)^–1]^–1(b₁–t₂)

=t₂.                                                                 (13.1.35)

Следовательно, в выражениях (13.1.16) и (13.1.17) для оценки факторов во втором (а=3) опыте скорейшего улучшения отклика надо использовать соответствующие элементы вектора b₃, а не вектора b₁.

В данной процедуре оценки факторов для опытов скорейшего улучшения отклика, если на определённый параметр  не накладывается ограничение, то в выражениях (13.1.32) и (13.1.34) необходимо использовать результат b_j его оценки. А при расчёте доверительных интервалов факторов по формулам (13.1.30) и (13.1.31) для а=2, 3,... должны использоваться соответствующие элементы векторов b₂, b₃,…, b_а.

Интервалы предсказания результатов опытов

В основанном на линейной модели (13.1.20) методе скорейшего улучшения отклика можно делать предсказания значений переменных отклика в опытах его скорейшего улучшения. Если в этих опытах устанавливаются найденные по формулам (13.1.14) значения нормированных факторов, то предсказания переменных отклика в них можно делать по формуле (13.1.18). Однако реальные значения факторов в опытах скорейшего улучшения отклика могут отличаться от найденных по формулам (13.1.16) и (13.1.17). Поэтому эти реальные значения необходимо нормировать по формуле (13.1.1) и получить векторы х_а реальных значений нормированных факторов в этих опытах. Таким образом, более корректно оцениваемые ожидаемые значения нормированных переменных отклика в опытах скорейшего улучшения отклика находятся по формуле =х_а^Тb. Векторы х_а не являются строками матрицы X₁ модели (13.1.20), но, если элементы этих векторов будут сильно отличаться от соответствующих элементов строк матрицы X₁, то предсказания могут сильно отличаться от измеряемых значений переменных отклика в этих опытах.

В разделе 9.5 рассмотрен метод нахождения интервалов предсказания будущих наблюдений. Этот метод применим и для нахождения интервалов предсказания значений нормированных переменных  отклика, соответствующих векторам х_а факторов в опытах скорейшего улучшения отклика.

Для нахождения интервала предсказания результата одного опыта используется модель

=х_а^Т+ε,

где  - вектор параметров модели (13.1.20) и предсказание переменной  делается по формуле =х_а^Тb₁, что является также результатом оценки ожидаемого её значения E()=х_а^Т. Случайные величины  и  независимы, так как переменная  предсказания считается независимой от п нормируемых наблюдаемых переменных отклика начального эксперимента, используемых для вычисления . Поэтому дисперсия разности – получается в виде

D(–)=D(–х_а^Тb₁)

=D(х_а^Т+e –х_а^Тb₁).

Так как х_а^Т является постоянной, то имеем

D(–)=D(e)+D(х_а^Тb₁)

=s²+s²х_а^Т(X₁^ТX₁)^–1х_а

=s²[1+х_а^Т(X₁^ТX₁)^–1х_а],

что можно оценить выражением s²[1+х_а^Т(X₁^ТX₁)^–1х_а].

Математическое ожидание Е(–) =Е(х_а^Т+e –х_а^Тb₁)=0, так как Е(e)=0 и Е(b₁)=, а результат s² оценки дисперсии не зависит от  и =х_а^Тb₁. Таким образом, здесь статистика t_у получается в виде

t_у=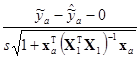

и имеет распределение t(п–р). А то, что с вероятностью 1–α её значения находятся в интервале между –t_α/2(п–р) и t_α/2(п–р) можно записать так

Pr[–t_α/2(п–р)≤≤t_α/2(п–р)]=1–α.

Чтобы получить 100(1–α)% интервал предсказания значений переменной  неравенство в квадратных скобках преобразуем к виду

Бесплатная лекция: "3.12 Ахроматические и хроматические контуры" также доступна.

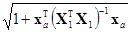–t_α/2(п–р)s≤≤+t_α/2(п–р)s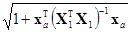

и, учитывая, что =х_а^Тb₁, получаем выражение для этого интервала

х_а^Тb₁±s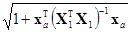t_α/2(п–р).                                    (13.1.36)

Заметим, что доверительная вероятность 1–α для этого интервала предсказания имеет место только для одного набора значений элементов вектора х_а. Так что для результата каждого опыта скорейшего улучшения отклика будет свой интервал предсказания.

Для получения интервала предсказания в натуральных единицах измерений необходимо преобразовать нормированную переменную отклика в натуральные единицы измерений по формуле (13.1.18). И если в эту формулу вместо  подставить (13.1.36), то получаем выражение для интервала предсказания значений переменных отклика в опытах скорейшего улучшения отклика в виде

+S_у[х_а^Тb₁±s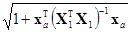t_α/2(п–р)].                        (13.1.37)