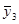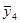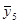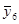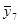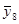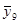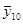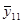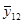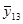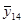Анализ эксперимента по плану 2 в 4 степени
11.3. Анализ эксперимента по плану 24
При небольшом числе факторов общее число опытов в эксперименте по плану 2р довольно большое. Например, по плану 25 в эксперименте будут 32 опыта, по плану 26 эксперимент состоит из 64 опытов, а по плану 210 эксперимент включает уже 1024 опыта. Выделяемые для проведения эксперимента средства обычно ограничены, так что часто выполнить все опыты можно только один раз, как в примере эксперимента с пневматическим прибором из предыдущего раздела. Выполненный так эксперимент называют экспериментом без повторения опытов. По результатам эксперимента стараются оценить не только воздействия факторов и их взаимодействий на отклик, но и ошибки результатов оценки. Однако без повторения опытов дисперсию ошибок эксперимента можно оценить только с использованием постулируемой модели. В разделе 7.3 показано, что несмещённую оценку дисперсии s2 можно сделать, используя вектор несмещённой оценки параметров этой модели.
Кроме этого, по результатам такого эксперимента нельзя проверить адекватность постулируемой модели. Для проверки адекватности модели в разделе 6.4 некоторые опыты эксперимента повторялись. Поэтому в данном разделе рассмотрим эксперимент, в котором все опыты повторялись несколько раз. Этот эксперимент из области чистовой токарной обработки заготовок на станке с числовым программным управлением (ЧПУ).
Шероховатость поверхности является наиболее важной характеристикой качества многих изделий получаемых на токарных станках в машиностроении. При планировании процесса токарной обработки, вместе с заданием допуска на размер, требование к шероховатости является одним из важнейших ограничений. Проанализируем результаты исследований, проведённых с целью выяснения влияния на шероховатость поверхности при токарной обработке таких факторов, как твёрдость материала обрабатываемой заготовки, скорость продольной подачи, угол при вершине резца в плане, глубина резания и скорость вращения шпинделя станка [Feng (2001); Feng, Wang (2002)]. При этом радиус закругления вершины резца оставался постоянным и равным 0,819 мм.
Для выяснения степени влияния рассматриваемых факторов на переменные отклика, являющиеся средними арифметическими измеряемых шероховатостей поверхностей обработанных заготовок, был поставлен отсеивающий эксперимент. Эксперимент по дробному факторному плану 25–1 разрешающей способности V имел шестнадцать опытов в виде определённых операций токарной обработки [Feng (2001)]. Все опыты этого эксперимента выполнялись в случайной последовательности с повторением каждого три раза, и получаемые значения шероховатости записывались в микронах.
Эксперимент и его результаты
Регрессионным анализом данных показано, что твердость материала обрабатываемой заготовки, скорость продольной подачи, угол при вершине резца в плане и скорость резания оказывают существенное влияние на шероховатость поверхности [Feng (2001)]. Четыре взаимодействия между двумя разными факторами также значительно влияют на шероховатость. Однако фактор "глубина резания", принимавший в эксперименте значения 0.51mm и 1.02mm, не имел существенного влияния. Поэтому, исключая этот фактор, статистическую модель зависимости шероховатости от указанных выше факторов можно построить на основе результатов эксперимента выполняемого по полному факторному плану 24 [Боков (2016)].
В опытах эксперимента требуемые по плану токарные работы выполнялись на цилиндрических заготовках длиной 76,2 мм и диаметром 31,75 мм. Твёрдость 86 HRB материала заготовок на верхнем уровне этого фактора обеспечивалась выбором в качестве материала никель-хром-молибденовой цементированной стали (AISI 8620), а твёрдость 52HRB материала заготовок на нижнем уровне этого фактора обеспечивалась выбором алюминиевого сплава (типа AD-33). В резцах использовались вставные твердосплавные (режущие) пластины с покрытием углеродно-нитридным титаном Ti (C, N), Al2O3 и TiN (карболой класса TP200). Угол при вершине резца в плане на верхнем уровне был 80º, а на нижнем уровне составлял 35º.
Опыты проводились на токарном станке с ЧПУ типа YAM CK-1. Скорость вращения шпинделя станка на верхнем уровне устанавливалась равной 1500 об/мин, а на нижнем уровне была равной 1000 об/мин. Скорость продольной подачи на верхнем уровне устанавливалась равной 0,127 мм/об, а на нижнем уровне была 0,051 мм/об.
Рекомендуемые материалы
Измерения шероховатости поверхности обработанных заготовок проводились с использованием профилометра Митутойо типа SJ-301. Три измерения выполнялись вдоль оси каждой обработанной заготовки по её обработанной поверхности, и каждое измерение отстояло приблизительно на 120° по спирали в последовательности один за другим. Усреднённое значение этих трёх измерений представляло наблюдаемое значение арифметического среднего шероховатости поверхности.
В рассматриваемом эксперименте по плану 24 все опыты подлинно повторялись три раза. Под подлинными повторениями опыта подразумевается то, что вариация между выполняемыми при одинаковых условиях опытами эксперимента является отражением общей изменчивости от опыта к опыту. Рандомизация последовательности выполнения всех 48 опытов эксперимента гарантирует, что повторения являются подлинными. Но выполнение этого не всегда бывает легким. Для данного эксперимента опыт включал: (1) наладку станка, (2) загрузку программы обработки заготовки в соответствии с планом эксперимента, (3) установку на станке заготовки из требуемого по плану материала (4) выполнение токарной обработки при всех факторах, установленных на соответствующих уровнях для этого опыта и (5) измерение шероховатости поверхности обработанной заготовки. Подлинное повторение опытов означает выполнение всех этих операций для всех 48 опытов. Повторение только измерений шероховатости поверхности обработанной заготовки в каждом опыте дало бы только оценку дисперсии измерений. Обычно это только малая часть дисперсии эксперимента от опыта к опыту. Для выполнения оценки дисперсии ошибок эксперимента, результат которой используется для нахождения стандартной ошибки результата оценки отдельного воздействия, каждый опыт эксперимента должен подлинно повторяться. Результаты выполненных таким образом в случайной последовательности 48 опытов представлены в таблице 11.3.1 элементами векторов у1, у2, у3, а вектор 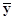 состоит из усреднённых значений результатов повторений всех опытов.
состоит из усреднённых значений результатов повторений всех опытов.
Таблица 11.3.1. Компоновка факторов и данные отклика эксперимента по плану 24
| Опыты | x1 | x2 | x3 | x4 | у1 | у2 | у3 |
|
| 1 | –1 | –1 | –1 | –1 | у1,1 | у1,2 | у1,3 |
|
| 2 | +1 | –1 | –1 | –1 | у2,1 | у2,2 | у2,3 |
|
| 3 | –1 | +1 | –1 | –1 | у3,1 | у3,2 | у3,3 |
|
| 4 | +1 | +1 | –1 | –1 | у4,1 | у4,2 | у4,3 |
|
| 5 | –1 | –1 | +1 | –1 | у5,1 | у5,2 | у5,3 |
|
| 6 | +1 | –1 | +1 | –1 | у6,1 | у6,2 | у6,3 |
|
| 7 | –1 | +1 | +1 | –1 | у7,1 | у7,2 | у7,3 |
|
| 8 | +1 | +1 | +1 | –1 | у8,1 | у8,2 | у8,3 |
|
| 9 | –1 | –1 | –1 | +1 | у9,1 | у9,2 | у9,3 |
|
| 10 | +1 | –1 | –1 | +1 | у10,1 | у10,2 | у10,3 |
|
| 11 | –1 | +1 | –1 | +1 | у11,1 | у11,2 | у11,3 |
|
| 12 | +1 | +1 | –1 | +1 | у12,1 | у12,2 | у12,3 |
|
| 13 | –1 | –1 | +1 | +1 | у13,1 | у13,2 | у13,3 |
|
| 14 | +1 | –1 | +1 | +1 | у14,1 | у14,2 | у14,3 |
|
| 15 | –1 | +1 | +1 | +1 | у15,1 | у15,2 | у15,3 |
|
| 16 | +1 | +1 | +1 | +1 | у16,1 | у16,2 | у16,3 |
|
Линейной регрессионной моделью моделируют зависимость наблюдаемых переменных отклика, то есть измеряемых шероховатостей поверхностей обработанных заготовок в опытах эксперимента, от указанных выше четырёх факторов и их взаимодействий. При анализе данных эксперимента по плану 24 кроме воздействий самих четырёх факторов необходимо рассматривать шесть воздействий от взаимодействий двух факторов, четыре воздействия от взаимодействий трёх факторов и одно воздействие от взаимодействия четырёх факторов. Поэтому матрица линейной модели для анализа этого эксперимента состоит их элементов, показанных в таблице 11.3.2. Это матрица Адамара и в ней все столбцы уровней взаимодействий факторов получены в результате произведений Адамара столбцов уровней факторов, номера которых показаны в подстрочных индексах взаимодействий.
Таблица 11.3.2. Матрица полной модели для эксперимента по плану 24
| x0 | x1 | x2 | x3 | x4 | x12 | x13 | x14 | x23 | x24 | x34 | x123 | x124 | x134 | x234 | x1234 |
| +1 | –1 | –1 | –1 | –1 | +1 | +1 | +1 | +1 | +1 | +1 | –1 | –1 | –1 | –1 | +1 |
| +1 | +1 | –1 | –1 | –1 | –1 | –1 | –1 | +1 | +1 | +1 | +1 | +1 | +1 | –1 | –1 |
| +1 | –1 | +1 | –1 | –1 | –1 | +1 | +1 | –1 | –1 | +1 | +1 | +1 | –1 | +1 | –1 |
| +1 | +1 | +1 | –1 | –1 | +1 | –1 | –1 | –1 | –1 | +1 | –1 | –1 | +1 | +1 | +1 |
| +1 | –1 | –1 | +1 | –1 | +1 | –1 | +1 | –1 | +1 | –1 | +1 | –1 | +1 | +1 | –1 |
| +1 | +1 | –1 | +1 | –1 | –1 | +1 | –1 | –1 | +1 | –1 | –1 | +1 | –1 | +1 | +1 |
| +1 | –1 | +1 | +1 | –1 | –1 | –1 | +1 | +1 | –1 | –1 | –1 | +1 | +1 | –1 | +1 |
| +1 | +1 | +1 | +1 | –1 | +1 | +1 | –1 | +1 | –1 | –1 | +1 | –1 | –1 | –1 | –1 |
| +1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 | +1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 |
| +1 | +1 | –1 | –1 | +1 | –1 | –1 | 1 | +1 | –1 | –1 | +1 | –1 | –1 | +1 | +1 |
| +1 | –1 | +1 | –1 | +1 | –1 | +1 | –1 | –1 | +1 | –1 | +1 | –1 | +1 | –1 | +1 |
| +1 | +1 | +1 | –1 | +1 | +1 | –1 | +1 | –1 | +1 | –1 | –1 | +1 | –1 | –1 | –1 |
| +1 | –1 | –1 | +1 | +1 | +1 | –1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 | –1 | +1 |
| +1 | +1 | –1 | +1 | +1 | –1 | +1 | +1 | –1 | –1 | +1 | –1 | –1 | +1 | –1 | –1 |
| +1 | –1 | +1 | +1 | +1 | –1 | –1 | –1 | +1 | +1 | +1 | –1 | –1 | –1 | +1 | –1 |
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Анализ эксперимента по усреднённым результатам опытов
Если бы опыты этого эксперимента выполнялись без повторений, то их результатами можно считать усреднённые значения в столбце 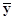 таблицы 11.3.1. В этом случае модель для анализа такого эксперимента со всеми взаимодействиями факторов постулируется так
таблицы 11.3.1. В этом случае модель для анализа такого эксперимента со всеми взаимодействиями факторов постулируется так
 =β0+β1x1+β2x2+β3x3+β4x4+β12x12+β13x13+β14x14+β23x23+β24x24+β34x34
=β0+β1x1+β2x2+β3x3+β4x4+β12x12+β13x13+β14x14+β23x23+β24x24+β34x34
+β123x123+β124x124+β134x134+β234x234+β1234x1234+e,
где коэффициенты β с соответствующими подстрочными индексами - параметры модели, а нормированные факторы x1 –твёрдости материала заготовок, x2 –скорости продольной подачи, x3 - угла при вершине резца, x4 - скорости вращения шпинделя и e - ошибка опыта. При выбранных выше верхних и нижних уровнях включённых в модель факторов, их нормированные значения находятся по формуле (2.6.4), как и в (11.2.1). В матричном виде модель записывается так
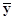 =Xоβо+e, (11.3.1)
=Xоβо+e, (11.3.1)
где матрица Хо дана в таблице 11.3.2, вектор 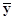 приведён в таблице 11.3.1, βо - вектор параметров модели и e - вектор ошибок опытов эксперимента.
приведён в таблице 11.3.1, βо - вектор параметров модели и e - вектор ошибок опытов эксперимента.
В предыдущем разделе показано, что при двухуровневом плане эксперимента его линейная модель имеет параметры, являющиеся фактически воздействиями факторов и их взаимодействий на переменные отклика. Поэтому, считая верными допущения раздела 7.1, где Е(у)=Xq заменяется на Е(у)=Xоβо, методом наименьших квадратов можно найти вектор оценки параметров модели (11.3.1) по формуле
 = (XоTXо)–1XоT
= (XоTXо)–1XоT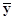 . (11.3.2)
. (11.3.2)
А если воспользоваться полученными в результате выполнения эксперимента числовыми значениями переменных отклика [Feng (2001)], то вектор оценки параметров получается
 = [1,354 –0,201 0,084 –0,089 –0,229 0,038 –0,237 0,054 0,020 0,048 0,151
= [1,354 –0,201 0,084 –0,089 –0,229 0,038 –0,237 0,054 0,020 0,048 0,151
0,031 0,050 0,057 –0,104 –0,022]. (11.3.3)
На основе результатов 16 опытов эксперимента по плану 24 невозможно оценить дисперсию ошибок эксперимента, но обоснованным предположением может быть то, что некоторые результаты оценки воздействий от взаимодействий (т.е., параметров модели) получаются, в основном, из-за шума и поэтому их можно считать множеством результатов для сравнения с остальными результатами оценки параметров.
При анализе воздействий на основе данных факторных экспериментов без повторения опытов появляются две трудности: (1) иногда получаются большие результаты оценки воздействий от взаимодействий высокого порядка и (2) необходимо предусматривать отбор воздействий. Графическое изображение результатов оценки воздействий в виде рассмотренного в разделе 1.6 графика кумулятивных вероятностей их распределения может обеспечить эффективный путь преодоления обеих трудностей. Такие графики строятся обычно с использованием компьютерных программ. Например, в программе Mathcad эти графики строятся следующим образом.
На графике кумулятивных вероятностей распределения каждое значение данных строится в зависимости от такого его значения, которое имело бы нормальное распределение. Рассмотрим те элементы вектора (11.3.3), которые представляют результаты оценки воздействий только контролируемых факторов и их взаимодействий. Эти элементы обозначим вектором  . Ожидаемые нормальные значения, называемые нормальными подсчётами (N_Score), могут быть оценены вычислением сначала ранговых подсчётов сортированных данных. В Mathcad это делается так
. Ожидаемые нормальные значения, называемые нормальными подсчётами (N_Score), могут быть оценены вычислением сначала ранговых подсчётов сортированных данных. В Mathcad это делается так
j:=0..last( )
)
Effect:=sort( )
)
rj:=j+1
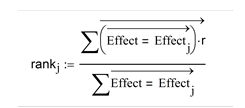
И, формируя пропорциональную оценку для каждого rankj получаемую по следующей формуле, называемой иногда формулой Van der Waerden,
pj:= ,
,
нормальные подсчёты являются соответствующими pj процентильными пунктами из стандартного нормального распределения
N_Scorej:=qnorm(pj,0,1)
Если выборка результатов оценки имеет нормальное распределение, то точки графика кумулятивных вероятностей будут выстраиваться приблизительно в прямую линию. График кумулятивных вероятностей распределения элементов вектора  показан на Рис.11.3.1.
показан на Рис.11.3.1.
Положим, что данные анализируемого эксперимента по плану 24 получились просто в результате случайной вариации около среднего и изменения уровней факторов не имели реального влияния на отклик. Тогда эти 15 результатов оценки воздействий, представляющих 15 контрастов между парами усреднённых переменных отклика, имели бы приблизительно нормальные распределения с центром в нуле и располагались бы на графике их кумулятивных вероятностей приблизительно по прямой линии. Однако на Рис.11.3.1 видно, что результаты оценки воздействий не все располагаются вдоль прямой. Довольно близко к прямой линии располагаются 8 результатов оценки, включая результат оценки воздействия от взаимодействия четырёх факторов. Это «линия ошибок», так как образующие её результаты оценки таковы, что могли бы быть результатом только шума. Однако остальные результаты оценки резко отклоняются от этой линии и не объясняются случайным происхождением. Поэтому может быть резонным допущение, что восемь результатов оценки по линии ошибок в основном из-за шума и поэтому составляют множество для сравнения с остальными результатами оценки.
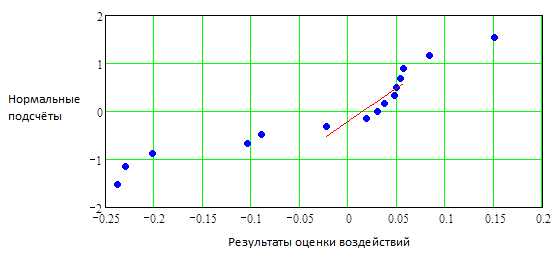
Рис.11.3.1. График кумулятивных вероятностей распределения для результатов оценки воздействий
В это множество для сравнения входят результаты оценки воздействий от взаимодействий двух  =0,038,
=0,038,  =0,054,
=0,054,  =0,020,
=0,020,  =0,048, трёх
=0,048, трёх  =0,031,
=0,031,  =0,050,
=0,050,  =0,057 и четырёх
=0,057 и четырёх  =–0,022, факторов. Так как математические ожидания этих результатов оценки равны нулю, то их совместная оценка дисперсии выполняется по формуле
=–0,022, факторов. Так как математические ожидания этих результатов оценки равны нулю, то их совместная оценка дисперсии выполняется по формуле
(СОО)2=( 2+
2+ 2+
2+ 2+
2+ 2+
2+ 2+
2+ 2+
2+ 2+
2+ 2)/8=1,781х10–3
2)/8=1,781х10–3
и является квадратом стандартной ошибки (СОО) результатов оценки воздействий остальных факторов и их взаимодействий. Поэтому СОО= =0,042.
=0,042.
Эту стандартную ошибку результатов оценки воздействий факторов и их взаимодействий, не объясняемых шумом, можно найти также методом рассмотрения модели с этими факторами и их взаимодействиями. Она постулируется так
 =β0+β1x1+β2x2+β3x3+β4x4+β13x13+β34x34+β234x234+e
=β0+β1x1+β2x2+β3x3+β4x4+β13x13+β34x34+β234x234+e
или в матричном виде
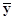 =Xβ+e, (11.3.4)
=Xβ+e, (11.3.4)
где X - матрица уровней факторов и отобранных их взаимодействий, а β - вектор параметров этой модели. Вектор оценки этих параметров методом наименьших квадратов находится по формуле  = (XTX)–1XT
= (XTX)–1XT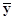 и получается
и получается
 =[1,354 –0,201 0,084 –0,089 –0,229 –0,237 0,151 –0,104]. (11.3.5)
=[1,354 –0,201 0,084 –0,089 –0,229 –0,237 0,151 –0,104]. (11.3.5)
Сумма квадратов остатков для этой модели находится по формуле
SE= [I–X(XTX)–1XT]
[I–X(XTX)–1XT]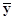 =0,228
=0,228
и из выражения (7.3.8) несмещённая оценка дисперсии получается s2=SE/8=0,029. Обратная матрицы XTX
(XTX)–1= .
.
Отсюда оценка дисперсии для результатов оценки параметров делается по формуле 0,063s2=1,796х10–3, а стандартная ошибка результатов оценки параметров, равная корню квадратному из результата оценки их дисперсии, получается равной 0,042. Это значение совпадает с полученным методом множества для сравнения.
В итоге перечень результатов оценки параметров модели (11.3.4) с их стандартными ошибками показан в таблице 11.3.3. В ней все абсолютные величины результатов оценки, по крайней мере, в два раза больше стандартной ошибки. Поэтому эти воздействия факторов и их отобранных взаимодействий являются реальными и отличны от шума.
Таблица 11.3.3. Результаты оценки параметров со стандартными ошибками для данных эксперимента по плану 24
| Нормированные факторы и их взаимодействия | Результаты оценки параметров со стандартными ошибками |
| Фактор твёрдости материала заготовки, х1 | –0,201±0,042 |
| Фактор скорости продольной подачи, х2 | 0,084±0,042 |
| Фактор угла при вершине резца, х3 | –0,089±0,042 |
| Фактор скорости вращения шпинделя, х4 | –0,229±0,042 |
| Взаимодействие двух факторов х1 и х3 | –0,237±0,042 |
| Взаимодействие двух факторов х3 и х4 | 0,151±0,042 |
| Взаимодействие трёх факторов х2, х3 и х4 | –0,104±0,042 |
Из таблицы 11.3.3 также видно, что все факторы эксперимента взаимодействуют друг с другом. Поэтому они должны рассматриваться вместе. Можно также графически представить взаимодействия факторов, как было сделано на Рис.11.2.2. При этом взаимодействие трёх факторов х2, х3 и х4 можно рассматривать как взаимодействие фактора х2 с взаимодействием двух факторов х3 и х4.
Построение и анализ графика кумулятивных вероятностей для распределения оценок воздействий является важным в отборе воздействий, не относящихся к шуму. Другой графический метод отбора воздействий предложен в [Lenth, (1989)]. Его описание можно найти также в [Box с соавт. (2005) стр. 203].
Для правильного использования статистических методов информация о результатах оценки воздействий факторов и их взаимодействий с возможной ошибкой должна анализироваться совместно с имеющимися знаниями предметной области. Графические методы дают ценные средства, позволяющие информации в данных и знаниям предметной области соответствующим образом взаимодействовать. Например, для используемых уровней факторов рассматриваемого эксперимента специалист по чистовой токарной обработке мог и не подозревать о таких больших воздействиях от взаимодействий двух факторов х1 и х3, х3 и х4, а также трёх факторов х2, х3 и х4.
Анализ эксперимента с учётом повторных опытов
В результате анализа эксперимента с использованием его полной линейной модели (11.3.1) установлено, что из всех взаимодействий факторов только воздействия от взаимодействий двух факторов х1 и х3, х3 и х4, а также трёх факторов х2, х3 и х4, имеют выделяющиеся из шума результаты оценки. Поэтому дальнейший анализ эксперимента с учётом повторных опытов имеет смысл проводить с использованием функции линейной модели (11.3.4). Все опыты эксперимента повторялись трижды, следовательно, с учётом повторных опытов эта модель в матричном виде записывается так
у=СXβ+e, (11.3.6)
где у= - вектор всех измеренных значений шероховатости, С=
- вектор всех измеренных значений шероховатости, С= - матрица преобразования размеров тхп и ранга п=16, при т=3п=48, X - матрица модели, состоящая из уровней нормированных факторов и их отобранных взаимодействий с первым столбцом из единиц, как показано в таблице 11.3.2, β - вектор параметров модели и e - вектор ошибок эксперимента, которые, полагается, распределены нормально в виде N(0, Is2). В таблице 11.3.4 уровни факторов и опыты размещены в стандартном порядке. Матрица С состоит из трёх единичных матриц, так как все опыты повторялись трижды. Но если опыты повторяются не одинаковое число раз, то матрица С формируется в соответствии с числом повторений каждого опыта, например, как показано в разделе 6.4.
- матрица преобразования размеров тхп и ранга п=16, при т=3п=48, X - матрица модели, состоящая из уровней нормированных факторов и их отобранных взаимодействий с первым столбцом из единиц, как показано в таблице 11.3.2, β - вектор параметров модели и e - вектор ошибок эксперимента, которые, полагается, распределены нормально в виде N(0, Is2). В таблице 11.3.4 уровни факторов и опыты размещены в стандартном порядке. Матрица С состоит из трёх единичных матриц, так как все опыты повторялись трижды. Но если опыты повторяются не одинаковое число раз, то матрица С формируется в соответствии с числом повторений каждого опыта, например, как показано в разделе 6.4.
Таблица 11.3.4. Матрица модели для эксперимента по плану 24
| Опыты | x0 | x1 | x2 | x3 | x4 | x13 | x34 | x234 |
| 1 | +1 | –1 | –1 | –1 | –1 | +1 | +1 | –1 |
| 2 | +1 | +1 | –1 | –1 | –1 | –1 | +1 | –1 |
| 3 | +1 | –1 | +1 | –1 | –1 | +1 | +1 | +1 |
| 4 | +1 | +1 | +1 | –1 | –1 | –1 | +1 | +1 |
| 5 | +1 | –1 | –1 | +1 | –1 | –1 | –1 | +1 |
| 6 | +1 | +1 | –1 | +1 | –1 | +1 | –1 | +1 |
| 7 | +1 | –1 | +1 | +1 | –1 | –1 | –1 | –1 |
| 8 | +1 | +1 | +1 | +1 | –1 | +1 | –1 | –1 |
| 9 | +1 | –1 | –1 | –1 | +1 | +1 | –1 | +1 |
| 10 | +1 | +1 | –1 | –1 | +1 | –1 | –1 | +1 |
| 11 | +1 | –1 | +1 | –1 | +1 | +1 | –1 | –1 |
| 12 | +1 | +1 | +1 | –1 | +1 | –1 | –1 | –1 |
| 13 | +1 | –1 | –1 | +1 | +1 | –1 | +1 | –1 |
| 14 | +1 | +1 | –1 | +1 | +1 | +1 | +1 | –1 |
| 15 | +1 | –1 | +1 | +1 | +1 | –1 | +1 | +1 |
| 16 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 |
Модель (11.3.6) содержит линейную функцию вектора β неизвестных параметров, а элементами её матрицы X являются уровни нормированных факторов и их отобранных взаимодействий. В этом случае, как показано в предыдущем разделе, параметры модели выражают воздействия соответствующих им факторов на переменные отклика. По теореме Гаусса-Маркова оценка параметров получается наилучшей, если она выполняется методом наименьших квадратов. Однако для такой оценки вектора β необходимо соблюдение допущений раздела 7.1, где Е(у)=Xq нужно заменить на Е(у)=СXβ. Тогда формула оценки вектора β имеет вид
 = (XTСTСX)–1XTСTR
= (XTСTСX)–1XTСTR
=(XTX)–1XTСTR/3. (11.3.7)
В числовом виде, если воспользоваться полученными значениями переменных отклика [Feng (2001)], то вектор оценки параметров получается в виде
 = [1,354 –0,201 0,084 –0,089 –0,229 –0,237 0.151 –0,104],
= [1,354 –0,201 0,084 –0,089 –0,229 –0,237 0.151 –0,104],
который совпадает с вектором оценки в (11.3.5). Таким образом, функция линейной модели для зависимости результатов  оценки ожидаемых значений переменных отклика от рассматриваемых нормированных факторов и их взаимодействий принимает вид
оценки ожидаемых значений переменных отклика от рассматриваемых нормированных факторов и их взаимодействий принимает вид
 =1,354–0,201x1+0,084x2–0,089x3–0,229x4–0,237x13+0,151x34–0,104x234. (11.3.8)
=1,354–0,201x1+0,084x2–0,089x3–0,229x4–0,237x13+0,151x34–0,104x234. (11.3.8)
Диагностическая проверка модели
В разделе 8.4 отмечено, что остатки играют важную роль в диагностической проверке модели. Вектор остатков для модели (11.3.6) находится по формуле  =у–
=у– , где вектор оценки ожидаемых значений переменных отклика
, где вектор оценки ожидаемых значений переменных отклика  =СX
=СX . Построение графика кумулятивных вероятностей распределения остатков даёт диагностическую проверку любой модели эксперимента. Причём на этом же графике можно построить прямую линейной функции, аппроксимирующей зависимость нормальных подсчётов от элементов вектора остатков с использованием метода наименьших квадратов. Результаты этих построений показаны на Рис.11.3.2.
. Построение графика кумулятивных вероятностей распределения остатков даёт диагностическую проверку любой модели эксперимента. Причём на этом же графике можно построить прямую линейной функции, аппроксимирующей зависимость нормальных подсчётов от элементов вектора остатков с использованием метода наименьших квадратов. Результаты этих построений показаны на Рис.11.3.2.
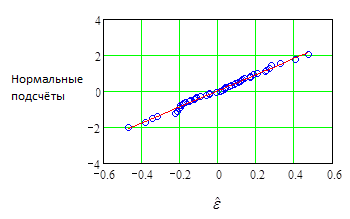
Рис.11.3.2. График кумулятивных вероятностей распределения остатков и аппроксимирующая прямая линия
Все значения остатков на Рис.11.3.2 располагаются вблизи или прямо по прямой линии, подтверждая предположение, что все не включённые в модель (11.3.6) воздействия от взаимодействий факторов легко объясняются случайным шумом. Эта проверка является полезной, так как подтверждает, что только три из всех воздействий от взаимодействий факторов действительно влияют на переменные отклика.
Кроме этого, если значения остатков выстраиваются приблизительно в прямую линию, то соблюдается допущение нормальности распределения ошибок эксперимента. На Рис.11.3.2 не видно отклонения от нормального распределения. Однако необходимо также удостовериться, что и дисперсия ошибок не изменяется с изменением значений переменных отклика. Для этого используется показанный на Рис.11.3.3 график зависимости остатков от соответствующих элементов вектора оценки ожидаемых значений переменных отклика. На этом рисунке остатки рассеяны случайно, что подтверждает постоянство величины дисперсии для всех измеренных в эксперименте значений переменных отклика.
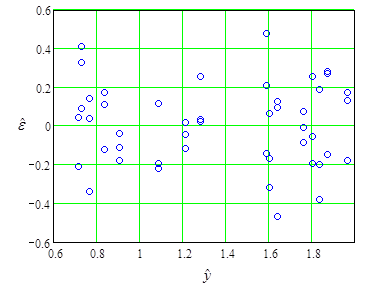
Рис.11.3.3. График зависимости остатков от результатов оценки ожидаемых значений переменных отклика.
Однако если величина дисперсии зависит от значений переменных отклика, то этот график покажет воронкообразный рисунок. Это наводит на мысль о необходимости преобразования переменных отклика [Myers с соавт. (2016) стр. 37]. Рекомендуется также построение графиков остатков в зависимости от порядка их получения и от уровней факторов. И если на этих графиках значения остатков выстраиваются не в случайном порядке, то это указывает на отклонение распределения ошибок от нормального закона и преобразование переменных отклика может способствовать достижению нормальности.
Проверка значимости регрессии
В разделе 9.1 показано, что проверка значимости регрессии заключается в проверке гипотезы H0: β1=0, где в данном случае β1Т= [β1, β2, β3, β4, β13, β34, β234]. Для этой проверки используется статистика FRc, расчёт которой выполняется по приведённым в таблице 9.1.1 формулам. Однако в этих формулах не учитывается повторение опытов. Поэтому для расчёта статистики FRc необходимы формулы с учётом повторений опытов.
Для получения таких формул разделим матрицу Х в виде [1п, X1], а вектор β соответственно в виде  . Тогда модель (11.3.6) можно записать так
. Тогда модель (11.3.6) можно записать так
у= [С1п, СX1] +e. (11.3.9)
+e. (11.3.9)
Аналогично выражению (7.5.28), нормальные уравнения для этой модели записываются в виде
[С1п, СX1]Т[С1п, СX1] =[С1п, СX1]Тy. (11.3.10)
=[С1п, СX1]Тy. (11.3.10)
Произведение [С1п, СX1]Т[С1п, СX1] в левой части можно преобразовать так
[С1п, СX1]Т[С1п, СX1] = [С1п, СX1]=
[С1п, СX1]= ,
,
так как С1п=1т. Матрица СTС диагональная с элементами по диагонали равными числу повторений опытов. Все опыты повторялись трижды, поэтому диагональ состоит из чисел 3. В силу (П.2.21) и (П.2.22), можно поменять местами матрицы СTС и X1, а также СTС и 1, и записать последнее выражение в виде
 =
= =
= ,
,
так как 1тТ1т=m. Взаимодействия факторов сами можно рассматривать в качестве новых нормированных факторов. Поэтому, как показано после (7.5.29), имеем 1ТX1=0Т.
Правую часть выражения (11.3.10) можно записать в виде
[1т, СX1]Тy= y=
y= =
=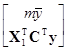 .
.
На основании полученного оценка параметров модели методом наименьших квадратов даётся матричным выражением
 ={[1т, СX1]Т[1т, СX1]}–1[1т, СX1]Тy
={[1т, СX1]Т[1т, СX1]}–1[1т, СX1]Тy
=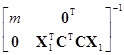
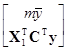 =
=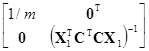
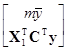
=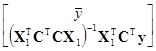
или отдельными формулами
 =
= (11.3.11)
(11.3.11)
и
 = (X1TСTСX1)–1X1TСTу
= (X1TСTСX1)–1X1TСTу
=(X*TX*)–1X*Tу, (11.3.12)
где X*=СX1.
Как и в (9.1.1), скорректированная усреднённым значений переменных отклика сумма квадратов STс= может быть разделена в виде
может быть разделена в виде
STс= ТX*Tу+[
ТX*Tу+[ –
– ТX*Tу]
ТX*Tу]
= ТX*Tу+SE [в силу (7.5.35)]
ТX*Tу+SE [в силу (7.5.35)]
=SRс+SE. (11.3.13)
где SRс= ТX*Tу - образующаяся в результате регрессии и скорректированная усреднённым сумма квадратов. Подставляя в выражение для SRс вместо
ТX*Tу - образующаяся в результате регрессии и скорректированная усреднённым сумма квадратов. Подставляя в выражение для SRс вместо  его выражение по формуле (11.3.12), получаем SRс в виде квадратичной формы
его выражение по формуле (11.3.12), получаем SRс в виде квадратичной формы
SRс=уТX*(X*TX*)–1X*Tу
Для процедуры проверки гипотез на основе имеющей распределение F статистики представим и остальные суммы квадратов выражения (11.3.13) в виде квадратичных форм относительно вектора у. Это необходимо для того чтобы, используя теоремы главы 5, показать, что суммы SRс и SE имеют распределения хи-квадрат и статистически независимы. Так как сумма  =yТ(I–Е/т)y и SE=
=yТ(I–Е/т)y и SE= –
– ТX*Тy, то (11.3.13) можно записать так
ТX*Тy, то (11.3.13) можно записать так
yТ(I–Е/т)y=SRс+SE
=уТX*(X*TX*)–1X*Tу+yТ(I–Е/т)y–уТX*(X*TX*)–1X*Tу
=yТH*y+yТ(I–Е/т–H*)y, (11.3.14)
где H*=X*(X*TX*)–1X*T.
По теореме 9.1.1 матрицы I–Е/т, H*=X*(X*TX*)–1X*T и I–Е/т–H* обладают следующими свойствами: произведение H*(I–Е/т)=H*, матрица H* идемпотентная и ранга р–1, матрица I–Е/т–H* идемпотентная и ранга т–р, а произведение H*[I–Е/т–H*]=О.
По теореме 9.1.2, если вектор у имеет нормальное распределение Nm(СXβ, s2I), то SRс/s2= ТX*ТX*
ТX*ТX* /s2 имеет нецентральное распределение c2(р–1, γ1) с параметром не центральности γ1=β1ТX*ТX*β1/(2s2), а SE/s2=[
/s2 имеет нецентральное распределение c2(р–1, γ1) с параметром не центральности γ1=β1ТX*ТX*β1/(2s2), а SE/s2=[ –
– ТX*ТX*
ТX*ТX* ]/s2 имеет центральное распределение c2(т–р). Кроме этого, по теореме 9.1.3 квадратичные формы SRc=yТH*y и SE=yТ(I–Е/т–H*)y статистически независимы.
]/s2 имеет центральное распределение c2(т–р). Кроме этого, по теореме 9.1.3 квадратичные формы SRc=yТH*y и SE=yТ(I–Е/т–H*)y статистически независимы.
Далее по теореме 9.1.4 статистика
FRc= =
= (11.3.15)
(11.3.15)
приобретает следующие распределения:
Ø Если гипотеза H0: β1=0 ложна, то статистика FRc имеет нецентральное распределение F(р–1, т–р, γ1) с параметр не центральности γ1=β1ТX*ТX*β1/(2s2).
Ø Если гипотеза H0: β1=0 верна, то параметр γ1=0 и статистика FRc принимает центральное распределение F(р–1, т–р).
По этой статистике проверка гипотезы H0: β1=0 осуществляется так. Эта гипотеза ложна, если значение статистики FRc больше критического значения Fкp случайной переменной, имеющей центральное распределение F(p–1, т–p), при выбранной 1–α интегральной вероятности на интервале от 0 до Fкp.
По аналогии с таблицей 9.1.1, сведём расчёт статистики FRc по полученным здесь формулам в таблицу 11.3.5. В результате, проверка гипотезы H0: β1=0 по статистике FRс показывает, что полученное значение статистики FRс=26,41 больше критического значения Fкр=2,249 случайной переменной, имеющей центральное распределение F(7, 40) и равную 0,95 интегральную вероятность на интервале от 0 до 2,249. Поэтому гипотеза H0: β1=0 ложна, и надо сделать вывод, что, по крайней мере, один элемент вектора β1 не равен нулю. Кроме этого, рекомендуется чтобы для адекватности оценки функции модели значение статистики FRс превосходило критическое значения Fкр в 10 раз [Box, Draper (2007) стр.281]. В данном случае FRс превосходит Fкр более чем в 10 раз, поэтому в результате оценки вектора параметров модели получена адекватная её функция.
Здесь проверка значимости регрессии показана для случая, когда все опыты эксперимента повторялись одинаковое число раз. В тех случаях, когда опыты не повторяются или повторяются не одинаковое число раз, можно пользоваться формулами раздела 9.1 и для повторяемых опытов брать их усреднённый результат.
Таблица 11.3.5. Расчёт статистике FRc для проверки гипотезы H0: β1=0
| Источники вариации | Суммы квадратов | Степени свободы | Средние квадратичные | Статистика проверки |
| Регрессия | SRс=9,471 | р–1=7 | SRс/(p–1)=1,353 | FRc= |
| Остатки | SE=2,049 | т–р=40 | SE/(т–p)=0,051 | |
| Итого | STс=11,520 | т–1=47 |
Проверка адекватности модели
Для того чтобы убедиться, что постулируемая функция модели обеспечивает приемлемую аппроксимацию истинной функции шероховатости поверхности, необходимо рассмотреть возможные доказательства адекватности модели. Проверка адекватности требует чтобы, по крайней мере, для одного набора уровней включённых в эксперимент факторов имелись реальные повторения опытов. В рассматриваемом эксперименте для каждого набора уровней факторов опыты выполнялись три раза с наблюдениями отклика, показанными в таблице 11.3.1. Повторные данные переменных отклика в виде элементов векторов у1, у2, у3 получались в результате подлинных повторений опытов на разных заготовках и при переналадках станка, а не просто повторением измерений шероховатости поверхности обработанных заготовок. Имея результаты так повторённых опытов, можно проверить является ли модель (11.3.6) адекватной, используя имеющую распределение F статистику.
Для этого, как и в разделе 6.4, представим приведённые в таблице 11.3.1 данные шероховатости поверхности в виде дисперсионной модели классификации по одному признаку
уij= +eij, (11.3.16)
+eij, (11.3.16)
где уij - значения шероховатости, полученные в опытах эксперимента (i=1, 2, ..., п и j=1, 2, 3),  - среднее переменной отклика трёх повторений i-го опыта и ошибки eij считается, что распределены нормально, независимо и одинаково в виде N(0, s2), где s2 дисперсия ошибок. Таким образом, полагается, что значения переменных отклика в подгруппах повторных опытов являются выборками из имеющих распределения N(
- среднее переменной отклика трёх повторений i-го опыта и ошибки eij считается, что распределены нормально, независимо и одинаково в виде N(0, s2), где s2 дисперсия ошибок. Таким образом, полагается, что значения переменных отклика в подгруппах повторных опытов являются выборками из имеющих распределения N( , s2) совокупностей наблюдений.
, s2) совокупностей наблюдений.
Рассмотренный в разделе 1.6 график кумулятивных вероятностей распределения может использоваться для проверки нормальности распределения большой выборки значений данных. В данном случае для выборки из 48 результатов опытов эксперимента построение этого графика позволяет выяснить имеют ли полученные данные эксперимента нормальное распределение. Эти данные на графике изображаются в зависимости от теоретического нормального распределения таким образом, чтобы точки данных формировали прямую линию. Отклонения от прямой линии указывают на отклонения от нормальности. На Рис.11.3.4 точки графика кумулятивных вероятностей распределения данных рассматриваемого эксперимента выстраиваются приблизительно в прямую линию. Поэтому можно считать, что эти данные имеют приблизительно нормальное распределение.
Кроме проверки, что данные эксперимента имеют нормальное распределение, перед использованием модели (11.3.16) необходимо также проверить является ли обоснованным сделанное допущение о равенстве дисперсий результатов в подгруппах повторных опытов. Для этого может использоваться, например, тест Левина [NIST/SEMATECH e-Handbook of Statistical Methods, раздел 1.3.5.10]. Этим тестом проверяется нулевая гипотеза H0: s12=s22=…=sп2 против альтернативной гипотезы, что по крайней мере одна пара дисперсий не равны.
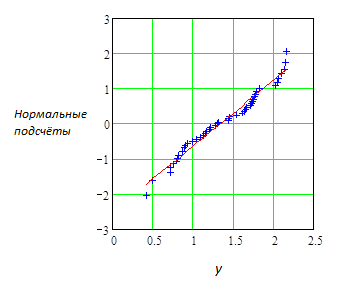
Рис. 11.3.4. График кумулятивных вероятностей распределения данных шероховатости поверхности (у), где Нормальные подсчёты являются шкалой стандартных отклонений от среднего.
Для выборки данных шероховатости поверхности анализируемого эксперимента объёмом 48, разделённой на 16 подгрупп с размером каждой подгруппы равным 3, тестовая статистика Левина находится по формуле
L= , (11.3.17)
, (11.3.17)
где δij получаются из выражения δij=|уij– |,
|,  - усреднённое i-й подгруппы для δij и
- усреднённое i-й подгруппы для δij и  - общее усреднённое для всех δij.
- общее усреднённое для всех δij.
По тесту Левина гипотеза равенства дисперсий ложна, если L > Fa(п–1, т–п,), где Fa(п–1, т–п,) - верхнее критическое значение распределения F(п–1, т–п) при уровне значимости α. Так как т=3п=48, то вычисление статистики этого теста дает L=1,611. А если взять значения 0,01, 0,05 и 0,10 уровня значимости α, то для этого теста критические значения распределения F со степенями свободы п–1=15 и т–п=32 получаются большими [L=1,611<F0,10(15, 32) =1,707< F0,05(15, 32) =1,992 < F0,01(15, 32) =2,655]. Это означает, что гипотеза равенства дисперсий верна.
В матричном виде модель (11.3.16) можно записать так
y=C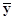 +e, (11.3.18)
+e, (11.3.18)
где 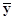 T= [
T= [ ,
,  , ...,
, ...,  ]. С учётом графика кумулятивных вероятностей для распределения данных шероховатости поверхности и результата теста Левина можно считать, что вектор e ошибок имеет распределение N(0, Is2), где I - единичная матрица ранга т. Оценка вектора
]. С учётом графика кумулятивных вероятностей для распределения данных шероховатости поверхности и результата теста Левина можно считать, что вектор e ошибок имеет распределение N(0, Is2), где I - единичная матрица ранга т. Оценка вектора 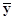 методом наименьших квадратов выполняется по формуле
методом наименьших квадратов выполняется по формуле
 = (СTС)–1СTу=СTу/3. (11.3.19)
= (СTС)–1СTу=СTу/3. (11.3.19)
Вектор  является вектором оценки средних наблюдаемых значений шероховатости поверхности в повторных опытах эксперимента. Для этой модели сумма SPE квадратов остатков находится из выражения
является вектором оценки средних наблюдаемых значений шероховатости поверхности в повторных опытах эксперимента. Для этой модели сумма SPE квадратов остатков находится из выражения
SPE= (у–С )Т(у–С
)Т(у–С )
)
=уT(I–HС)у, (11.3.20)
где матрица HС=С(СTС)–1СT. В разделе 6.4 отмечено, что при проверке адекватности модели эту сумму квадратов называют суммой квадратов чистых ошибок.
Из выражения (11.3.20) видно, что SРЕ является квадратичной формой относительно вектора у. Матрица I–HС является идемпотентной и дисперсия D(у)=Is2. Поэтому, так как SPE/s2=уT(I–HС)у/s2, то матрица (1/s2)(I–HС)Is2 также идемпотентная. Отсюда, так как вектор у ~ N(С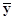 , Is2), то по следствию 2 теоремы 5.5 квадратичная форма уT(I–HС)у имеет нецентральное распределение χ2[ранг(I–HС), (С
, Is2), то по следствию 2 теоремы 5.5 квадратичная форма уT(I–HС)у имеет нецентральное распределение χ2[ранг(I–HС), (С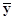 )T(I–HС)С
)T(I–HС)С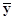 /2] и
/2] и
SPE/s2~χ2[ранг(I–HС), 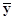 ТСT(I–HС)С
ТСT(I–HС)С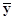 /(2s2)].
/(2s2)].
В этом выражении, при ранг(I)=т и ранг(С)=п, параметр не центральности обращается в нуль и нецентральное распределение χ2 сводится к центральному, так что
SPE/s2~χ2(т–n). (11.3.21)
По теореме 5.2.1, так как Е(у) =C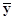 и D(у)=Is2, а матрица (I–HС) симметричная, то
и D(у)=Is2, а матрица (I–HС) симметричная, то
Е(SPE)=Е[уT(I–HС)у]=след[(I–HС)Is2]+(C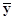 )Т(I–HС)C
)Т(I–HС)C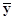
=s2след(I–HС)
=s2[след(I)–след(HС)] [в силу (П.11.1)]
=s2[т–ранг(HС)] [по теореме П.13.4]
=s2[т–ранг(С)] [по пункту 5 теоремы П.8.3]
=s2(т–п).
Следовательно, MSPE=SPE/(т–п) даёт несмещённую оценку дисперсии s2. Этот результат оценки дисперсии называют независящим от модели. Однако эта независимость распространяется только на те модели, которые можно построить на основе вектора у значений переменных отклика рассматриваемого эксперимента и для определённой матрицы С преобразования.
Для модели (11.3.6) сумма SE квадратов остатков является суммой квадратов отклонений наблюдаемых значений отклика у от их оцениваемых ожидаемых значений  =СX
=СX , то есть,
, то есть,
SE=(у–СX )T(у–СX
)T(у–СX ), (11.3.22)
), (11.3.22)
где  находится из (11.3.7). Таким образом, подставляя (11.3.7) в (11.3.22), имеем
находится из (11.3.7). Таким образом, подставляя (11.3.7) в (11.3.22), имеем
SE=уT(I–HX)у, (11.3.23)
где НХ=СX(XTСTСX)–1XTСT.
Произведение самого на себя вектора разности С –СX
–СX векторов оцениваемых ожидаемых значений шероховатости по моделям (11.3.18) и (11.3.6) известно как сумма SLF квадратов неадекватности. Эта сумма представляется выражением
векторов оцениваемых ожидаемых значений шероховатости по моделям (11.3.18) и (11.3.6) известно как сумма SLF квадратов неадекватности. Эта сумма представляется выражением
SLF= (С –СX
–СX )T(С
)T(С –СX
–СX ). (11.3.24)
). (11.3.24)
И, подставляя в него вместо  и
и  их выражения из (11.3.19) и (11.3.7), получаем
их выражения из (11.3.19) и (11.3.7), получаем
SLF =уT(HС–HX)у. (11.3.25)
Здесь SLF является квадратичной формой относительно у. Матрица HС–НХ идемпотентная и D(у)=Is2, поэтому матрица (1/s2)(HС–НХ)Is2 тоже идемпотентная. Таким образом, так как у ~ N(СXb, Is2), то по следствию 2 теоремы 5.5 квадратичная форма уТ(НС–НX)у имеет нецентральное распределение χ2[ранг(НС–НХ), (СXb)Т(НС–НХ)СXb/2] и, следовательно,
SLF/s2~χ2[ранг(HС–HX), bTXTСT(HС–HX)СXb/(2s2)]
~χ2[ранг(С)–ранг(X), (bTXTСTСXb–bTXTСTСXb)/(2s2)], (11.3.26)
что, при ранг(С)=n и ранг(X)=p, сводится к центральному распределению
SLF/s2~χ2(n–p) . (11.3.27)
По теореме 5.2.1, так как Е(у) =CXb и D(у)=Is2, а матрица (HС–НХ) симметричная, то
Е(SLF)=Е[уT(HС–HX)у]=след[(HС–НХ)Is2]+(CXb)Т(HС–НХ)CXb
=s2след(HС–HX)
=s2[след(HС)–след(HX)] [в силу (П.11.1)]
=s2[ранг(HС)–ранг(HX)] [по теореме П.13.4]
=s2[ранг(С)–ранг(X)] [по пункту 5 теоремы П.8.3 и пункту 1 теоремы П.4]
=s2(п–p).
Следовательно, MSLF=SLF/(п–p) также даёт несмещённую оценку дисперсии s2. Но эта оценка зависит от конкретной рассматриваемой модели, так как выражение (11.3.25) содержит матрицу Х этой модели. Квадратичную форму уT(HС–HX)у можно представить в виде уT(HС–HX)у=уT(HС–I+I–HX)у=уT(I–HX)у–уT(I–HС)у откуда
уT(I–HX)у=уT(I–HС)у+уT(HС–HX)у. (11.3.28)
Следовательно, сумма SE квадратов остатков равна сумме SPE квадратов чистых ошибок плюс сумма SLF квадратов неадекватности модели. А если взять математические ожидания левой и правой частей выражения (11.3.28), то имеем s2(т–р)=s2(т–п)+s2(п–p), что после сокращения s2 даёт (т–р)=(т–n)+(n–p). Отсюда число степеней свободы распределения хи-квадрат квадратичной формы SE равно сумме чисел степеней свободы распределений хи-квадрат квадратичных форм SPE и SLF.
В разделе 7.3 также установлено, что несмещенную оценку дисперсии s2 можно сделать по формуле (7.3.8), которая в данном случае, в силу (11.3.23), принимает вид
s2=уT(I–HX)у/(т–р). (11.3.29)
Таким образом, все квадратичные формы выражения (11.3.28) могут быть использованы для несмещённой оценки дисперсии s2, но результаты этих оценок получаются разными. Формула оценки spe2=SPE/(т–п) не содержит матрицы модели, а формула оценки slf2=SLF/(п–p) имеет меньше делитель, чем формула (11.3.29), и получается завышенной.
Поскольку произведения матриц (НС–НХ) и (I–НС) дают нулевую матрицу, то по следствию 1 теоремы 5.6.2 квадратичные формы SLF=уT(HС–HX)у и SPE=уT(I–HС)у статистически независимы. А две имеющие центральные распределения χ2 независимые квадратичные формы являются основой образования распределения F. То есть, если SLF имеет распределение χ2(n–p) и SPE имеет распределение χ2(т–n), то их отношение в виде [SLF/(n–p)]/[SPE/(т–n)] имеет распределение F со степенями свободы (n–p) и (т–n). Следовательно, для проверки адекватности модели имеющая это распределение статистика находится по формуле
FLF= [SLF/(n–p)]/[SPE/(т–n)]. (11.3.30)
Расчёт статистики FLF для проверки адекватности линейной регрессионной модели (11.3.6) для данных шероховатости поверхности [Feng (2001)] сведён в таблицу 11.3.4. И, поскольку уровень значимости α для этой проверки выбран равным 0,05, то статистика FLF получена меньше её критического значения [FLF=2,004<F0,05(8, 32,) =2,244]. Это значит, что линейная регрессионная модель (11.3.6) является адекватной.
Таблица 11.3.4. Проверка адекватности линейной регрессионной модели
| Источники дисперсии | Суммы квадратов, (mm)2 | Степени свободы | Средние квадратичные, (mm)2 | Статистика FLF |
| Неадекватность | SLF=0,684 | 8 | MSLF=0,086 | 2,004 |
| Чистые ошибки | SPE=1,365 | 32 | MSPE=0,043 | |
| Остатки | SE=2,049 | 40 |
Анализ модели давать предсказания
В разделе 8.6 показано, что сумма квадратов остатков предсказания может быть использована для оценки способности модели давать предсказания. В силу (8.6.11), эта сумма квадратов рассчитывается по формуле
Sop= =
= , (11.3.31)
, (11.3.31)
где элементы вектора  находятся по формуле (8.6.9). Для анализируемой модели в этой формуле элементами hii являются элементы диагонали матрицы HX. В данном случае все они равны 0,167. Поэтому расчёт вектора
находятся по формуле (8.6.9). Для анализируемой модели в этой формуле элементами hii являются элементы диагонали матрицы HX. В данном случае все они равны 0,167. Поэтому расчёт вектора  выполняется по формуле
выполняется по формуле  =
= /(1–0,167). График зависимости обычных остатков
/(1–0,167). График зависимости обычных остатков  от остатков
от остатков  показан на Рис.11.3.5. Точки на графике следуют вдоль прямой примерно с единичным наклоном. На нём нет удалённых от этой линии точек, указывающих на резко выделяющиеся значения.
показан на Рис.11.3.5. Точки на графике следуют вдоль прямой примерно с единичным наклоном. На нём нет удалённых от этой линии точек, указывающих на резко выделяющиеся значения.
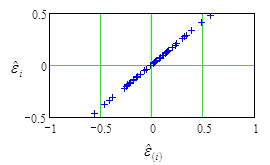
Рис.11.3.5. График зависимости обычных остатков  от остатков
от остатков  .
.
На основании найденного вектора  получаем Sop=2,951. Сумма квадратов остатков предсказаний используется для вычисления статистики Rp2 предсказания по формуле (8.6.12). В ней STс находится из выражения (11.3.13) и статистика предсказания получается Rp2=1–Sop/STс=0,744. На основании полученного результата можно ожидать, что модель (11.3.6) объяснит 74,4% изменений предсказываемых новых наблюдений шероховатости поверхности. Статистика предсказания получилась меньше статистики R2=SRc/STс=0,822 из раздела 6.4, представляющей описываемую функцией модели часть вариации значений переменных отклика относительно их средних значений. И для рассматриваемой модели статистика R2 показывает высокую меру достигнутой адекватности, так как максимально возможное значение статистики R2 получается Rmax2=(STс–SPE)/STс=0,881.
получаем Sop=2,951. Сумма квадратов остатков предсказаний используется для вычисления статистики Rp2 предсказания по формуле (8.6.12). В ней STс находится из выражения (11.3.13) и статистика предсказания получается Rp2=1–Sop/STс=0,744. На основании полученного результата можно ожидать, что модель (11.3.6) объяснит 74,4% изменений предсказываемых новых наблюдений шероховатости поверхности. Статистика предсказания получилась меньше статистики R2=SRc/STс=0,822 из раздела 6.4, представляющей описываемую функцией модели часть вариации значений переменных отклика относительно их средних значений. И для рассматриваемой модели статистика R2 показывает высокую меру достигнутой адекватности, так как максимально возможное значение статистики R2 получается Rmax2=(STс–SPE)/STс=0,881.
Упражнения
11.1. В результате постановки эксперимента по плану 24 по его результатам получены следующие результаты оценки воздействий факторов и их взаимодействий:
А=0,4; В= –7,6; С=14,1; D=66.7; АВ=16,7; АС=3,1; AD=5,2; BC=8,3; BD= –3,6; CD=14.3; АВС= –0,1; АBD= –4,7; ACD= 7,7; BCD= –2,3; АВСD=3,9.
Объясните результаты оценки с помощью графика кумулятивных вероятностей их распределения.
11.2. (a) Если выполняется эксперимент по плану 2p и каждый фактор устанавливается на уровнях –1 и +1, то какова взаимосвязь между результатами оценки воздействий факторов и коэффициентами регрессии модели первого порядка.
(б) Как в такой же ситуации взаимодействия двух фактора представляются в регрессионной модели?
11.3. Представьте, что отдельные опыты в составе факторного плана 23 выполняются последовательно в стандартном порядке (в полном пренебрежении к рандомизации!) в то время как, одновременно, игнорируемая экспериментатором четвертая переменная принимает значения, указанные в следующей таблице.
| х1 | х2 | х3 | х4 |
| –1 | –1 | –1 | –7 |
| +1 | –1 | –1 | 5 |
| –1 | +1 | –1 | 7 |
| +1 | +1 | –1 | 3 |
| –1 | –1 | +1 | –3 |
| +1 | –1 | +1 | –7 |
| –1 | +1 | +1 | –5 |
| +1 | +1 | +1 | 7 |
Если для модели первого порядка у=b0+b1х1+b2х2+b3х3+ε результаты оценки её параметров находятся методом наименьших квадратов, то определите смещение результатов оценки параметров модели, вызванное отсутствием члена b4х4 в модели.
11.4. Основная цель закалки стали это образование мартенсита. Переход из аустенита в мартенсит зависит от состава стали, который влияет на температуру образования мартенсита. Издавна считалось, что углерод и другие легирующие элементы понижают температурный диапазон, в котором образуется мартенсит. Предварительное исследование по факторному плану 23 для определения влияний углерода, марганца и никеля на ‘температуру начала образования мартенсита’ дало данные в следующей таблице.
| Факторы и их уровни | Начальная температура (oF) | ||
| C% | Mn% | Ni% | |
| 0,1 | 0,2 | 0,1 | 940 |
| 0,9 | 0,2 | 0,1 | 330 |
| 0,1 | 1,4 | 0,1 | 820 |
| 0,9 | 1,4 | 0,1 | 250 |
| 0,1 | 0,2 | 0,2 | 840 |
| 0,9 | 0,2 | 0,2 | 280 |
| 0,1 | 1,4 | 0,2 | 760 |
| 0,9 | 1,4 | 0,2 | 200 |
(а) Сделайте факторы нормированными.
(б) Нарисуйте схему плана и в соответствующих местах укажите значения отклика, то есть начальные температуры.
(в) Найдите все результаты оценки воздействий факторов, двухфакторных и трехфакторных взаимодействий.
(г) Допустим, что стандартное отклонение наблюдений отклика составляет s=65. Которые результаты оценки в (в) большие по сравнению с их стандартными ошибками?
(д) Каковы практические выводы из вашего анализа?
11.5. В приведённой ниже таблице данные получены в результате исследования влияния трех факторов: ξ1 - обороты в минуту (об/мин), ξ2 - осевая нагрузка вниз (вес, фунт) и ξ3 - скорость потока жидкости для сверления, на скорость (у) врезания сверла. Опыты представлены в случайном порядке, в котором они проводились. Пронормируйте факторы и определите тип используемого плана. Затем сделайте соответствующий анализ и перечислите полученные вами практические выводы.
| ξ1 | ξ2 | ξ3 | у |
| 110 | 2500 | 2 | 37,7 |
| 110 | 1000 | 2 | 25,6 |
| 60 | 2500 | 2 | 22,2 |
| 110 | 1000 | 7,3 | 36,6 |
| 110 | 1000 | 7,3 | 34,4 |
| 110 | 2500 | 7,3 | 49,1 |
| 60 | 1000 | 2 | 12,5 |
| 60 | 2500 | 2 | 21,0 |
| 110 | 2500 | 7,3 | 46,0 |
| 60 | 2500 | 7,3 | 33,5 |
| 110 | 1000 | 2 | 28,2 |
| 110 | 2500 | 2 | 39,2 |
| 60 | 1000 | 2 | 12,2 |
| 60 | 1000 | 7,3 | 19,5 |
| 60 | 2500 | 7,3 | 35,0 |
| 60 | 1000 | 7,3 | 20,8 |
11.6. Изготовитель бумажных пакетов желает проверить сопротивление (у) разрыву, для чего давно используется числовая шкала. Рассматриваются три фактора на каждом из двух нормированных уровнях, а именно: х1 - тип бумаги, х2 - влажность, х3 - направление разрыва, и получаются три повторных наблюдения, как показано в приведённой ниже таблице. (Для удобства опыты переставлены в стандартный порядок из случайного, в котором они выполнялись.) Общая сумма квадратов 496,87 для 24 наблюдений. Выполните факторный анализ данных, оцените s2 на основе результатов повторных опытов и сформулируйте выводы о факторах.
| х1 | х2 | х3 | Сопротивление разрыву | Суммы по строкам | ||
| –1 | –1 | –1 | 3,8 | 3,1 | 2,2 | 9,1 |
| +1 | –1 | –1 | 6,6 | 8,0 | 6,8 | 21,4 |
| –1 | +1 | –1 | 3,4 | 1,7 | 3,8 | 8,9 |
| +1 | +1 | –1 | 6,8 | 8,2 | 6,0 | 21,0 |
| –1 | –1 | +1 | 2,3 | 3,1 | 0,7 | 6,1 |
| +1 | –1 | +1 | 4,7 | 3,5 | 4,4 | 12,6 |
| –1 | +1 | +1 | 2,1 | 1,1 | 3,6 | 6,8 |
| +1 | +1 | +1 | 4,2 | 4,7 | 2,9 | 11,8 |
| Итого: | 97,7 |
11.7. Посмотрим еще раз на данные в упражнении 11.5. Оцените параметры модели первого порядка у=b0+b1х1+b2х2+b3х3+ε методом наименьших квадратов и выполните обычный анализ, включая анализ адекватности модели. Ваши выводы должны согласовываться с данными факторного анализа.
11.8. Посмотрим на данные упражнения 11.6. Мы могли бы формально использовать уравнение регрессии для анализа этих данных, но они гораздо более подходяще анализируются факторными методами. Почему?
11.9. Результаты оценки воздействий, полученные на основе данных выполненного по плану 25 эксперимента, следующие:
Е=–224 BCD=–18 BE=29
С=–153 ABDE=–14 DЕ=30
ABCDE=–77 D=–9 ABCE=31
ACE=–58 B=–6 BCE=39
AD=–54 CD=–4 ACDE=47
BC=–53 АВС=0 АС=53
ABD=–34 АE=2 АВСD=58
ACD=–33 BD=7 АВ=64
BDE=–28 CDE=12 СЕ=83
ABE=–22 BCDE=16 А=190
АDE=21
(а) Для этих результатов постройте график кумулятивных вероятностей их распределения.
(б) Какие воздействия вы думаете, отличаются от шума?
(в) Постройте график кумулятивных вероятностей нормального распределения оставшихся воздействий.
(г) Оцените стандартное отклонение результатов оценки по графику пункта (в).
[Частичный ответ: (б) E, C, A. (г) грубо 40]
11.10. (Источник: Wasiloff Е., Hargitt С. Using DOE to determine AA battery life, Quality Progress, Март 1999 г., cтр.67-71.) Срок службы двух типов батареек для игрушечных машин проверялся путём постановки факторного эксперимента по плану 23. Три фактора и их уровни были следующими:
1. Тип батареи: низкой стоимости (х1=–1), высокой стоимости (х1=+1).
2. Контакты разъема: стандартный Тамия (х2=–1), Дин позолоченный (х2=+1).
3. Начальная температура батареи: холодная (х3=–1), окружающей среды (х3=+1).
Откликом (у) в эксперименте было время разряда батарей в минутах. Полученные данные приведены в следующей таблице.
| Опыты | х1 | х2 | х3 | у |
| 1 | +1 | +1 | +1 | 493 |
| 2 | +1 | +1 | –1 | 490 |
| 3 | +1 | –1 | +1 | 489 |
| 4 | +1 | –1 | –1 | 612 |
| 5 | –1 | +1 | +1 | 94 |
| 6 | –1 | +1 | –1 | 75 |
| 7 | –1 | –1 | +1 | 93 |
| В лекции "4.3 Виды культуры" также много полезной информации. 8 | –1 | –1 | –1 | 72 |
Проанализируйте данные и сделайте выводы о том, как срок службы батареи зависит от трех факторов и их взаимодействий.