Последовательность и ее предел
Лекция 2
Последовательность и ее предел.
Комплексное число  называется пределом последовательности:
называется пределом последовательности:  (или последовательность сходится к точке
(или последовательность сходится к точке  :
:  ), если
), если 
выполнено  .
.
Теорема. Для того чтобы последовательность 
 {
{ } необходимо и достаточно
} необходимо и достаточно  .
.
Доказательство провести самостоятельно, используя неравенство треугольника ( ) и теорему Пифагора (
) и теорему Пифагора (

 ).
).
Из теоремы следует, что многие свойства последовательностей действительных чисел могут быть перенесены на последовательности комплексных чисел.
Функция комплексной переменной.
Рекомендуемые материалы
|
| Пусть произвольной точке |
Комплексное число  , как всякое комплексное число, имеет действительную и мнимую части
, как всякое комплексное число, имеет действительную и мнимую части  . Это – действительная
. Это – действительная  и мнимая
и мнимая  части функции.
части функции.
Пример. Выделим действительную и мнимую части функции  .
.

Элементарные функции комплексной переменной.
Экспонента  и при комплексных z сохраняет свои основные свойства
и при комплексных z сохраняет свои основные свойства
 .
.
Формула Эйлера  справедлива и для комплексных чисел z. Это будет показано позже. Используя четность cosz, chz и нечетность sinz, shz, (для комплексных z это тоже будет показано позже), получим формулы связи экспоненты с с тригонометрическими и гиперболическими синусами и косинусами.
справедлива и для комплексных чисел z. Это будет показано позже. Используя четность cosz, chz и нечетность sinz, shz, (для комплексных z это тоже будет показано позже), получим формулы связи экспоненты с с тригонометрическими и гиперболическими синусами и косинусами.  . Складывая и вычитая
. Складывая и вычитая  , получим
, получим
 .
.
Гиперболические косинус и синус определяются аналогично функциям действительной переменной
 .
.
Отсюда  .
.
Получим формулы связи тригонометрических и гиперболических косинусов и синусов.


Покажем, что функции  - функции периодические с периодом
- функции периодические с периодом  .
.
 ,
,
 имеют тот же период
имеют тот же период  , так как они являются линейной комбинацией
, так как они являются линейной комбинацией  - периодических функций с периодом
- периодических функций с периодом  .
.
Покажем, что функции  - функции периодические с периодом
- функции периодические с периодом  .
.
 .
.
 имеют тот же период
имеют тот же период  , так как они являются линейной комбинацией
, так как они являются линейной комбинацией  - периодических функций с периодом
- периодических функций с периодом  .
.
Упражнение. Выведите формулы



 ,
,
используя свойства экспоненты и полученные выше формулы.
Пример. Вычислить sin ( +5i), tg (
+5i), tg ( )
)
sin ( +5i) = sin
+5i) = sin cos5i + cos
cos5i + cos sin5i = sin5i = ch5
sin5i = sin5i = ch5

Логарифмическая функция.
Функция  определяется как обратная функция по отношению к функции
определяется как обратная функция по отношению к функции  . Пусть
. Пусть  ,
,  .
.
Тогда 
 .
.
Так как  , то, переходя в последнем соотношении к модулям, имеем
, то, переходя в последнем соотношении к модулям, имеем  ,
,  .
.
Аргументы левой и правой части в соотношении могут отличаться на  , поэтому
, поэтому  . Поэтому
. Поэтому
 .
.
Это – многозначная функция. Ее главная ветвь
 - функция однозначная.
- функция однозначная.
Пример. Вычислить ln(-1), Ln(-1), ln(1+i).
Ln(-1) = ln |-1| + iarg (-1) +  =
=  +
+ , ln(-1) =
, ln(-1) = 
ln(1+i) = ln|1+i| + iarg(1+i) =  .
.
Предел и непрерывность функции.
Комплексное число b называется пределом функции f(z) при  ,
,
 .
.
Это определение – то же, что определение предела функции действительной переменной с той лишь разницей, что модуль здесь имеет смысл расстояния на комплексной плоскости, а не на действительной прямой, как раньше. Кроме того, окрестность точки – не интервал с центром в этой точке, а круг без границы с центром в этой точке.
Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если  .
.
Функция  называется непрерывной в области G, если она непрерывна в каждой точке этой области.
называется непрерывной в области G, если она непрерывна в каждой точке этой области.
Область M называется областью однолистности функции  , если
, если 
Линейная функция  осуществляет линейное отображение комплексной плоскости на себя.
осуществляет линейное отображение комплексной плоскости на себя.  . Отсюда видно, что линейное отображение сводится к растяжению в
. Отсюда видно, что линейное отображение сводится к растяжению в  раз и повороту на
раз и повороту на  комплексной плоскости. Здесь область однолистности – вся плоскость.
комплексной плоскости. Здесь область однолистности – вся плоскость.
Инверсия  (
( ) переводит все точки, лежащие вне единичной окружности
) переводит все точки, лежащие вне единичной окружности  внутрь и наоборот. Точки
внутрь и наоборот. Точки  остаются на месте, единичная окружность отображается на себя.
остаются на месте, единичная окружность отображается на себя.
Отображение  (
( ) часть действительной оси (
) часть действительной оси ( ) и верхнюю полуплоскость отображает на всю плоскость. Часть действительной оси (
) и верхнюю полуплоскость отображает на всю плоскость. Часть действительной оси ( ) и нижняя полуплоскость тоже отображаются на всю плоскость. Здесь две области однолистности. Поэтому обратная функция
) и нижняя полуплоскость тоже отображаются на всю плоскость. Здесь две области однолистности. Поэтому обратная функция  двузначна.
двузначна.
Упражнение. Покажите, что при отображении  существует n областей однолистности. Выделите их. Функция
существует n областей однолистности. Выделите их. Функция  поэтому n – значна.
поэтому n – значна.
Отображение  переводит прямую, параллельную мнимой оси (
переводит прямую, параллельную мнимой оси ( ) в
) в  - окружность с центром в начале координат, радиусом
- окружность с центром в начале координат, радиусом  . Прямая, параллельная действительной оси
. Прямая, параллельная действительной оси  переводится в
переводится в  - луч из начала координат под углом y к действительной оси.
- луч из начала координат под углом y к действительной оси.
Поэтому полоса размером  вдоль действительной оси переводится во всю плоскость и представляет собой область однолистности (каждый отрезок в полосе, параллельный мнимой оси (x = a) отобразится в окружность радиуса a с центром в начале координат, меняя a, заполним этими окружностями всю плоскость). Следовательно, здесь бесконечное количество областей однолистности, а обратная функция
вдоль действительной оси переводится во всю плоскость и представляет собой область однолистности (каждый отрезок в полосе, параллельный мнимой оси (x = a) отобразится в окружность радиуса a с центром в начале координат, меняя a, заполним этими окружностями всю плоскость). Следовательно, здесь бесконечное количество областей однолистности, а обратная функция  - бесконечнозначна.
- бесконечнозначна.
Производная функции комплексной переменной вводится так же, как и для функции действительной переменной
 .
.
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее приращение в этой точке можно представить в виде
, если ее приращение в этой точке можно представить в виде
 , то есть
, то есть  - бесконечно малая при
- бесконечно малая при  . Главная линейная относительно
. Главная линейная относительно  часть приращения функции в точке
часть приращения функции в точке  ,
,  называется дифференциалом функции в точке
называется дифференциалом функции в точке  , (
, ( ).
).
Замечание. Функция двух переменных  называется дифференцируемой в точке (
называется дифференцируемой в точке ( ), если ее приращение в этой точке можно представить в виде
), если ее приращение в этой точке можно представить в виде

 +
+ +
+ ,
,
где  ,
,  - бесконечно малые при
- бесконечно малые при  ,
,
 ,
,  .
.
Теорема. Для того, чтобы функция  была дифференцируема в точке
была дифференцируема в точке  , необходимо и достаточно, чтобы существовала ее конечная производная в этой точке.
, необходимо и достаточно, чтобы существовала ее конечная производная в этой точке.
Доказательство. Проводится так же, как и для функции действительной переменной с использованием теоремы о связи функции, предела и бесконечно малой.
Необходимость. Пусть функция дифференцируема в точке  , тогда
, тогда
 ,
,
Делим обе части на 
 . Так как
. Так как  - бесконечно малая при
- бесконечно малая при  , то по теореме о связи функции, ее предела и бесконечно малой,
, то по теореме о связи функции, ее предела и бесконечно малой,  .
.
Поэтому  - формула для вычисления дифференциала.
- формула для вычисления дифференциала.
Достаточность. Пусть в точке  существует конечная производная функции
существует конечная производная функции  . Тогда по теореме о связи функции, предела и бесконечно малой
. Тогда по теореме о связи функции, предела и бесконечно малой  . Умножая на
. Умножая на  , получим
, получим  . Следовательно, функция дифференцируема в точке
. Следовательно, функция дифференцируема в точке  .
.
Функция называется дифференцируемой в области, если она дифференцируема в каждой точке этой области.
Теорема (Коши – Римана). Для того, чтобы функция  была дифференцируема в точке
была дифференцируема в точке  , необходимо и достаточно, чтобы ее действительная и мнимая части
, необходимо и достаточно, чтобы ее действительная и мнимая части  ,
,  были бы дифференцируемы в этой точке
были бы дифференцируемы в этой точке  как функции двух переменных
как функции двух переменных  и в этой точке выполнялись бы условия Коши – Римана
и в этой точке выполнялись бы условия Коши – Римана
 , причем
, причем  .
.
Замечание. С учетом условий Коши – Римана производная функции в точке может быть записана так:  =
= =
=
= =
=
Необходимость. Пусть функция дифференцируема в точке z0. Тогда
 .
.
Пусть  ,
,  .
.

 .
.
Отделяя действительную и мнимую части, имеем:

 ,
,

 .
.
Следовательно, функции  дифференцируемы в точке
дифференцируемы в точке 
Из первого соотношения следует, что

 .
.
Из второго соотношения следует, что
 ,
,  .
.
Поэтому 
 .
. 
 .
.
Достаточность. Пусть функции  дифференцируемы в точке
дифференцируемы в точке  и выполняются условия Коши – Римана.
и выполняются условия Коши – Римана.
 где
где  - бесконечно малые при
- бесконечно малые при  .
.
 .
.
Функции - бесконечно малые при
- бесконечно малые при  , поэтому они являются бесконечно малыми при
, поэтому они являются бесконечно малыми при  . Справедливы неравенства
. Справедливы неравенства  . Поэтому отношения приращений в двух последних скобках – ограниченные величины. Следовательно, выражения в двух последних скобках – бесконечно малые величины при
. Поэтому отношения приращений в двух последних скобках – ограниченные величины. Следовательно, выражения в двух последних скобках – бесконечно малые величины при  как произведения бесконечно малых на ограниченные. Обозначим два последних слагаемых
как произведения бесконечно малых на ограниченные. Обозначим два последних слагаемых 
 - бесконечно малая при
- бесконечно малая при  .
.
 .
.
Умножая это выражение на  , получим
, получим
 .
.
Следовательно, функция дифференцируема в точке  .
.
Условия Коши – Римана позволяют легко проверить дифференцируемость функции в точке.
Функция называется аналитической в области, если она дифференцируема в области.
Функция называется аналитической в точке, если она дифференцируема в этой точке и некоторой ее окрестности.
Основные элементарные функции  аналитические на всей комплексной плоскости.
аналитические на всей комплексной плоскости.
Проверим, например, условия Коши – Римана для функции 
Ещё посмотрите лекцию "КЛЮЧЕВСКИЙ Василий Осипович" по этой теме.
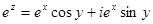
 Условия Коши – Римана выполнены при любых значениях переменных, функция аналитическая во всей комплексной плоскости.
Условия Коши – Римана выполнены при любых значениях переменных, функция аналитическая во всей комплексной плоскости.
Пример. Функция z = x не является дифференцируемой ни в одной точке, так как  .
.
Пример Функция  .
.
 . Функция дифференцируема только в точке z=0 и более ни в одной точке. Она не аналитическая ни в одной точке, поскольку для аналитичности кроме дифференцируемости в точке нужна еще дифференцируемость в некоторой области.
. Функция дифференцируема только в точке z=0 и более ни в одной точке. Она не аналитическая ни в одной точке, поскольку для аналитичности кроме дифференцируемости в точке нужна еще дифференцируемость в некоторой области.
Пример.  не является дифференцируемой ни в одной точке, так как условия Коши – Римана не выполнены,
не является дифференцируемой ни в одной точке, так как условия Коши – Римана не выполнены,  .
.




 поставлена в соответствие точка (единственная)
поставлена в соответствие точка (единственная)  (
( - две комплексных плоскости) по некоторому закону
- две комплексных плоскости) по некоторому закону  и областью значений в множестве
и областью значений в множестве  (или задано отображение области
(или задано отображение области  в область
в область  ).
).

















