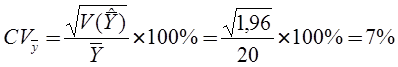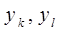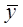Оценивание при расслоенном плане выборки
3. Оценивание при расслоенном плане выборки
Теорема 1.
При расслоенной случайном отборе суммарное Y и среднее  значения показателя оцениваются без смещения с помощью формул:
значения показателя оцениваются без смещения с помощью формул:
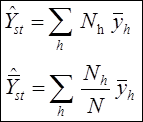
Доказательство.
Так как для каждой единицы, отобранной в слое h, выборочный вес равен:  , то для
, то для  -оценки суммарного значения имеем:
-оценки суммарного значения имеем:
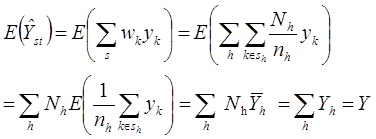
Замечания:
Рекомендуемые материалы
1. Расслоенная оценка среднего не равна среднему арифметическому значению, как при простом случайном отборе:
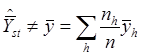
2. Расслоенный случайный отбор приводит к неравновероятностной выборке.
Теорема 2.
При расслоенном случайном отборе дисперсия оценок суммарного Y и среднего  значений показателя рассчитывается по формулам:
значений показателя рассчитывается по формулам:
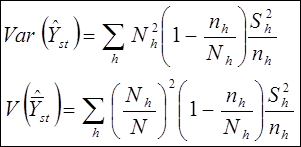
а их оценками соответственно будут
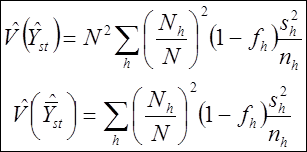
Доказательство:
В силу независимого характера простого случайного извлечения единиц в слоях для дисперсии оценки суммарного значения Y имеем:
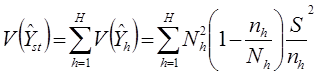
Второе утверждение теоремы следует из того, что при простом случайном отборе в h-ом слое дисперсия выборки ( ) является несмещенной оценкой дисперсии слоя (
) является несмещенной оценкой дисперсии слоя ( ).
).
Замечание.
Точность расслоенной оценки зависит только от дисперсии переменной внутри слоев. Поэтому расслоение эффективно, если  малы.
малы.
Пример 1.
| № единицы | (1) | (2) | (3) | (4) | (5) |
| Признак (y) | 13 | 15 | 17 | 25 | 30 |
| № слоя | {1} | {2} |
Случай простого случайного отбора.
Если отбирать простую случайную выборку объема 2 из всей совокупности {U}, то получим одну из 10 возможных выборок:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 13 15 | 13 17 | 13 25 | 13 30 | 15 17 | 15 25 | 15 30 | 17 25 | 17 30 | 25 30 |
|
| 14 | 15 | 19 | 21,5 | 16 | 20 | 22,5 | 21 | 23,5 | 27,5 |
Характеристики совокупности:


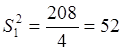
Коэффициент вариации признака (y):
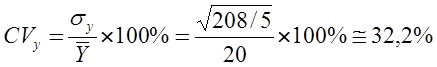
Вариация оценки среднего (объем выборки  ):
):
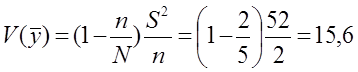
Коэффициент вариации оценки среднего:
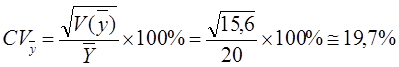
Случай расслоенного случайного отбора.
Характеристики слоев:


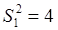


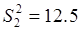
Из каждого слоя отбираем по одной единице (объем выборки  ). Всего возможно извлечь 6 выборок:
). Всего возможно извлечь 6 выборок:


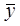
13 25 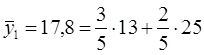
13 30 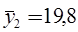
15 25 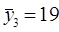
15 30 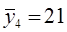
17 25 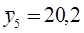
"Индивидуальное и историческое развитие" - тут тоже много полезного для Вас.
17 30 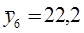
Вариация оценки среднего  :
:
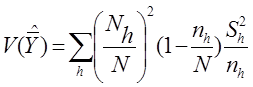
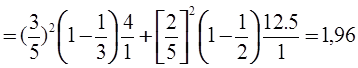
Коэффициент вариации оценки среднего: